3.1. Построение эпюр продольных сил - Центральное растяжение–сжатие кратко

Центральным растяжением (или сжатием) называется такой вид деформации, при котором в поперечных сечениях бруса возникает отличный от нуля только один внутренний силовой фактор – продольная сила, а все остальные внутренние силовые факторы равны нулю. Это бывает в случаях, когда линия действия равнодействующей внешних сил совпадает с продольной осью стержня.

Правило знаков: растягивающие продольные силы принято считать положительными, а сжимающие – отрицательными.

Для определения величины продольной силы Nиспользуется метод сечений, суть которого была рассмотрена в предыдущей главе. Покажем использование этого метода для рассматриваемого случая:

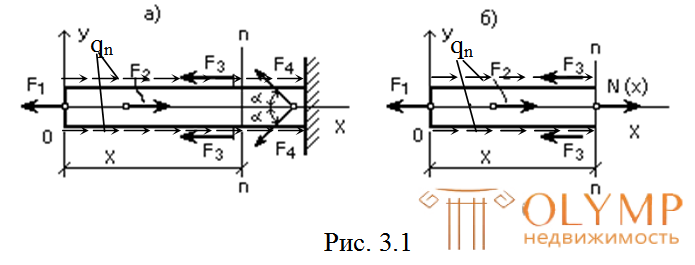
а) мысленно рассекаем брус сечением n–n(рис. 3.1а) на расстоянии х от выбранного начала координат. Начало координат можно помещать в начале каждого грузового участка (местная или локальная система координат) или оставлять в начале стержня (общая или глобальная система координат);

б) отбрасываем любую часть (рационально отбросить ту часть, на которую действует больше сил или ту, где имеется опора, но опорная реакция еще не определена);

в) заменяем действие отброшенной части продольной положительной (направленной от сечения, т.е. растягивающей) силой N(х) (рис. 3.1б);

г) составив уравнение равновесия рассматриваемой отсеченной части, определим величину продольной силы или ее функцию N(х). При этом полученное в результате положительное значение N соответствует растягивающей продольной силе, а отрицательное – сжимающей.

При использовании приведенного выше метода сечений необходимо иметь ввиду: если рассматривается равновесие части бруса, включающей в себя опорные связи, необходимо предварительно определить реакции опор, так как они относятся к разряду внешних сил.

Составим уравнение равновесия для части, изображенной на рис. 3.1б, из которого получаем выражение для определения продольной силы N(х) на данном грузовом участке:

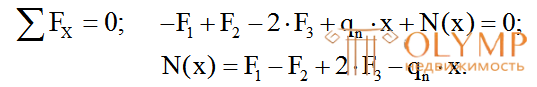
Если такие сечения проводить в пределах каждого грузового участка, то получим функции продольных сил на этих участках.

Часть бруса, в пределах которой закон изменения внутренних усилий описывается одним аналитическим выражением, называется грузовым участком.

Внешними признаками границ грузовых участков являются: места приложения внешних сосредоточенных усилий, места начала или окончания действия распределенной нагрузки, места изменения интенсивности распределенной нагрузки, в случае учета собственного веса бруса – места резкого изменения площади поперечного сечения.

Графики функций N(х) на грузовых участках, построенные в определенном масштабе, называются эпюрами продольных сил N. Они должны быть заштрихованы линиями перпендикулярно к продольной оси бруса и иметь знаки. Каждый штрих в масштабе представляет величину продольной силы N в данном сечении стержня. В случае отсутствия в пределах грузового участка распределенной нагрузки,N=const, т.е. эпюраNна таком участке постоянна.

ПРИМЕР 3.1

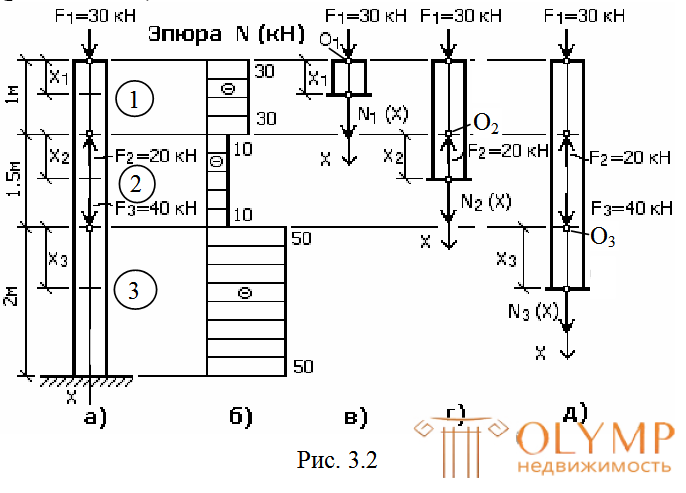
Требуется построить эпюру продольных сил для бруса, изображенного на рис. 3.2а.

РЕШЕНИЕ

1. Разобьем брус на грузовые участки 1, 2, 3. Границами грузовых участков здесь являются точки приложения сосредоточенных сил.

2. В пределах каждого участка проведем сечения на расстоянии x_iот начала грузового участка (рис. 3.2а), т.е. используем местную систему координат.

3. Отбросим нижнюю от сечения часть, тем самым исключив необходимость поиска реакции опоры. Действие отброшенной части заменим положительной (растягивающей) силой N_i(х), (рис. 3.2в, г, д).

4. На каждом грузовом участке составим уравнения равновесия рассматриваемой части бруса, из которых определим функции продольных сил N_i(х).

1-й грузовой участок (рис. 3.2в)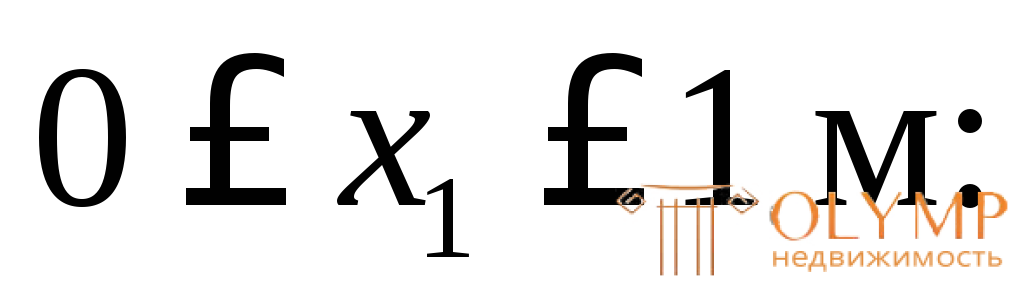

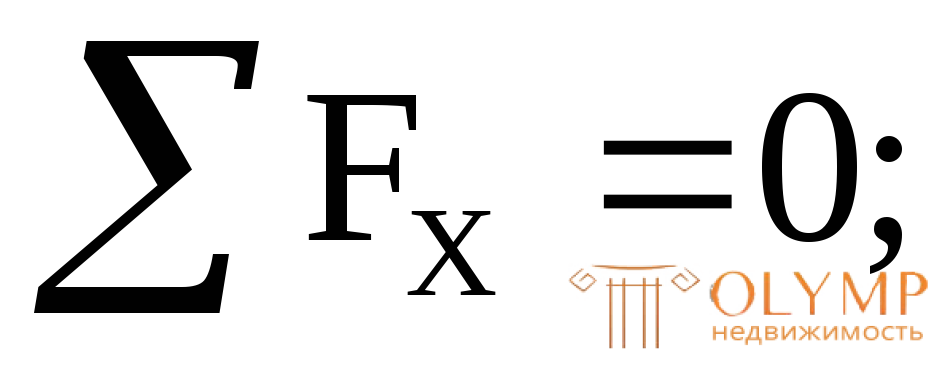
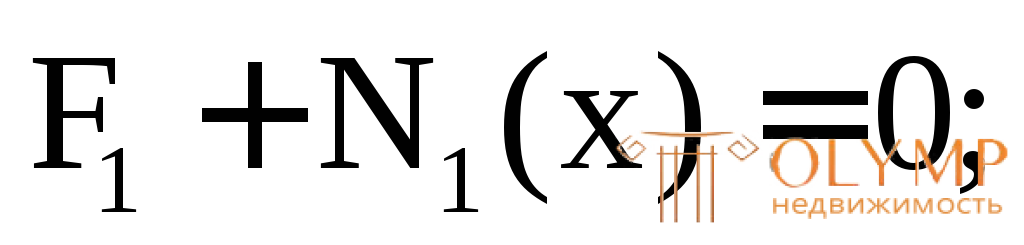
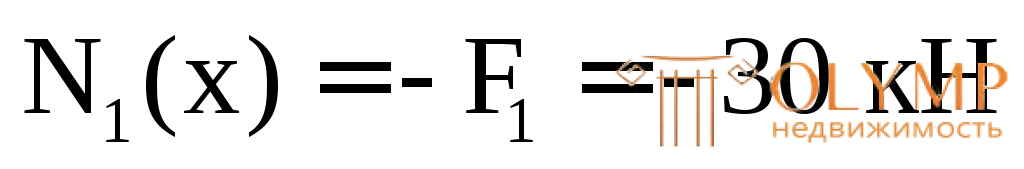(const).

2-й грузовой участок (рис. 3.2г)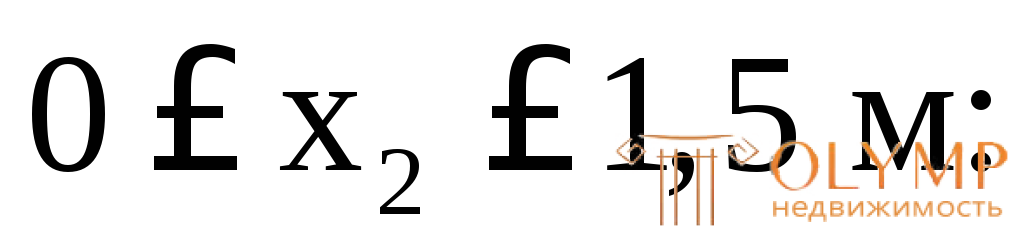

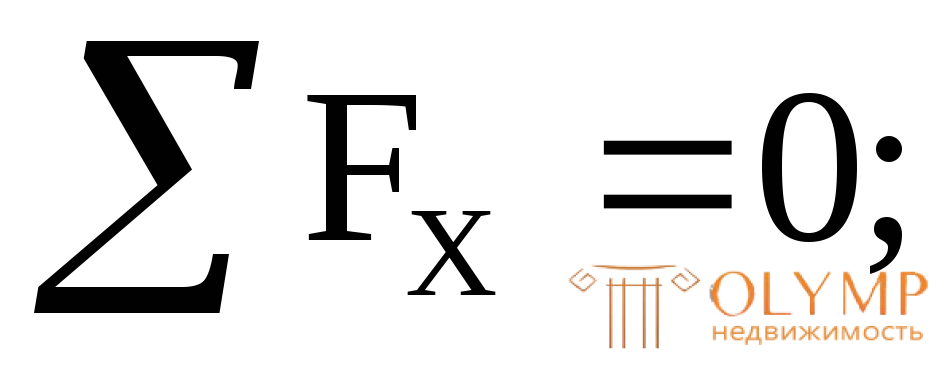
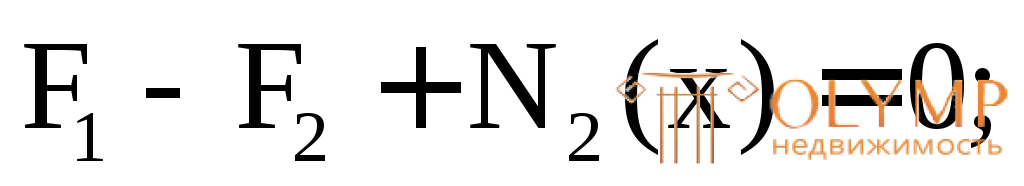
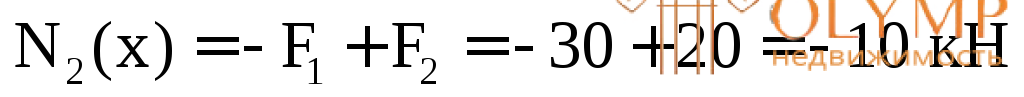(const).

3-й грузовой участок (рис. 3.2д)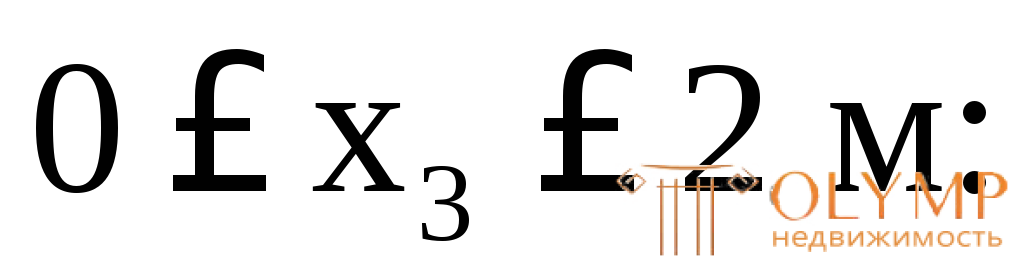

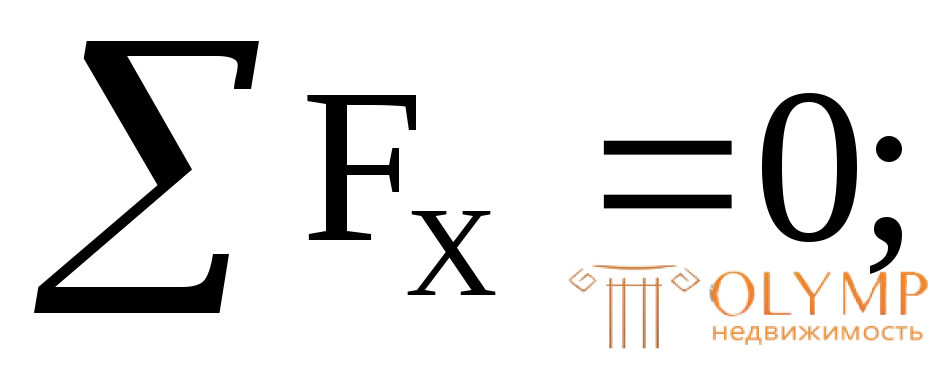
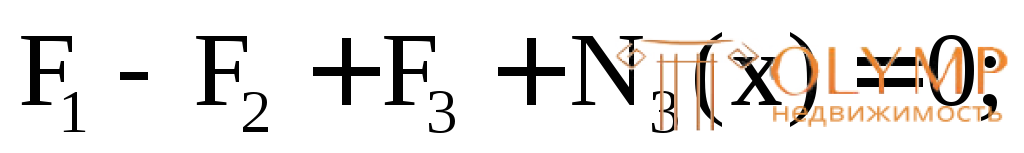
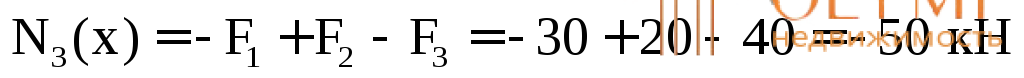(const).

По вычисленным значениям строим графики функции N(х) (эпюруN) на каждом участке, откладывая значения N перпендикулярно к продольной оси бруса (рис. 3.2б). Из эпюр видно,что в тех сечениях, где приложена внешняя сила F, действующая по продольной оси, на эпюре N имеется скачок, равный величине этой силы

Сформулируем рабочее правилодля определения величины продольной силы для стержней с прямолинейной осью, вытекающее из рассмотренного выше метода сечений:

продольная сила в любом поперечном сечении бруса численно равна алгебраической сумме проекций всех внешних сил, действующих по одну сторону от сечения, на продольную ось бруса в данном сечении.

При использовании этого правила необходимо обязательно учитывать принятое правило знаков для продольной силы.