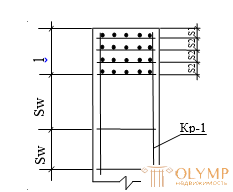
Indirect (local) reinforcement. Calculation example

Indirect reinforcement is a special transverse reinforcement, which can significantly increase the bearing capacity of compressed elements. Indirect reinforcement of rectangular elements is arranged in the form of often located welded meshes in the amount of not less than 4. Cross-linked nets are used to reinforce concrete under local compression in the zone of application of the greatest load. The essence of the work of indirect reinforcement is as follows: when a load is applied longitudinally, transverse tensile deformations occur in the elements, which lead to the formation of longitudinal cracks in the concrete. Indirect reinforcement works in tension and suppresses the lateral deformations of concrete, thereby increasing its bearing capacity. Indirect reinforced welded wire mesh is made of steel of classes АI, AIII and BpI ¯ 3 ... 10mm. The distance between the rods of the grids is taken from 45 to 100 mm.

The grids should be placed on a section called the reinforcement zone L, which is 10d, where d is the diameter of the longitudinal reinforcement. The distance to the 1st grid Sl is from 10 ... 40mm. The distance between the S2 grids is assigned as

(ranging from 60 to 150mm), so that it is divided by 3.

S2 = (L – S1) / 3

For example:

1) The diameter of the longitudinal reinforcement by calculation turned out to be 28mm.

Then the gain zone is L = 10d; L = 10 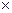Indirect (local) reinforcement. Calculation example 28 = 280mm.

Take S1 equal to 10mm or 40mm,

then S2 = (280-10) / 3 = 90mm or S2 = (280-40) / 3 = 80mm., which ranges from 60 to 150mm.

2) The diameter of the longitudinal reinforcement by calculation turned out to be 12mm.

Then the gain zone is L = 10d; L = 10 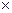Indirect (local) reinforcement. Calculation example 12 = 120mm.

Take S1 equal to 30mm,

then S2 = (120-30) / 3 = 30mm, which is less than the minimum distance of 60mm, therefore we take S2 equal to 60mm.

Type 1 task.

Given:

Ndl = 1000kN

Ncr = 500kN

l0 = 6.4m

b = h = 40cm

concrete B20, Indirect (local) reinforcement. Calculation example bi = 0.85

fittings 8¯18AII

Check the carrying capacity of the section

N £ Nsech

Decision.

Find in the printout:

Rb = 11.5 Indirect (local) reinforcement. Calculation example 0.85 = 9.78mPa

RSc = 280 MPa

A = 40 Indirect (local) reinforcement. Calculation example 40 = 1600cm2

N = 1000 + 500 = 1500kN

Asc = 20.36 cm2 (according to Table 7)

Formula 3 we find a = Rsс • Asc) / Rb • A

a = 280 • 20.36 / 9.78 • 1600 = 0.36

We find Ndl / N = 1000/1500 = 0.7; l = l0 / h = 640/40 = 16

jв = (0.82 + 0.76) /2=0.79 jж = (0.86 + 0.84) /2=0.85

j = jb + 2 (jj-jb) • a £ jj

j = 0.79 + 2 (0.85-0.79) 0.36 = 0.847 <0.85

Check the bearing capacity of the section according to the formula (1):

N £ j • (Rb • A + Rsc • Asc)

1500 £ 0.847 • (9.78 • 1600 + 280 • 20.36) (100) = 1808243Н = 1808kN

1500 < 1808

Conclusion: the carrying capacity of the section provided .

Type 2 task.

Given:

Ndl = 600kN

Ncr = 600kN

l0 = 4.2m

b = h = 30cm

concrete B20, Indirect (local) reinforcement. Calculation example i = 1

fittings AIII

Find Asc.

Decision.

Find in the printout:

Rb = 11.5 Indirect (local) reinforcement. Calculation example 1 = 11.5 mPa

RSc = 365mPa

A = 30 Indirect (local) reinforcement. Calculation example 30 = 900cm2

Set j = 1, define N = Ndl + Ncr

N = 600 + 600 = 1200kN

Find the approximate area of Asc reinforcement

Asc = N / j • Rss-A • Rb / Rsc = 1200 • 103/1 • 365 (100) -900 • 11.5 / 365 = 4.4 cm2

We find Ndl / N = 600/1200 = 0.5; l = l0 / h = 420/30 = 14

Indirect (local) reinforcement. Calculation example a = 4.4 • 365/900 • 11.5 = 0.159

we determine the coefficients jж = 0.88 and jв = 0.86 according to the table and

j = jb + 2 (jj-jb) • a £ jj j = 0.86 + 2 (0.88-0.86) • 0.159 = 0.924 ›0.88, therefore take jzh = jb = 0.88.

Finally we find the area of compressed reinforcement

Asc = 1200 • 103 / 0.88 • 365 (100) -900 • 11.5 / 365 = 8.6 cm2

Taken according to table 7 of Appendix 4¯18 AIII with Asc-fact. = 10.18 cm2

The transverse rods taken from the welding conditions in table 3 of the application

dw = 5ВрI with step Sw = 20d = 20 • 18 = 360mm

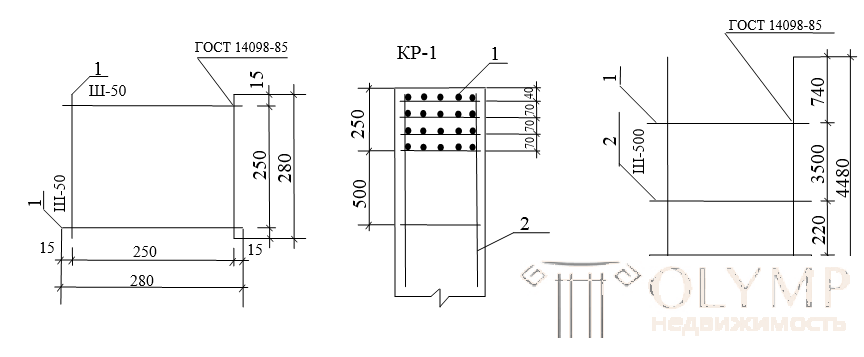
Indirect (local) reinforcement. Calculation example

L = 10b = 10 * 25 = 250

Sw = 20b = 20 * 25 = 500

S2 = 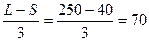Indirect (local) reinforcement. Calculation example

4500-20 = 4480-760 = 3720

3720: 500 * 7 = 3500

3720-3500 = 220

MARK	POSITION	NAME	QTY	MASS 1 DETAILS	MASS OF PRODUCT
KR-1	one	¯ 25АIII = 4480	2	17.24	35.47kg
KR-1	2	¯ 8А I = 280	9	0.11	35.47kg
S-1	one	¯ 8А I = 280	12	0.11	1,32 kg

0 25 = 3.85-4.48 = 17.24 0 8 = 0.395-0.28 = 0.11

SPECIFICATION OF COLUMN

pos.	designation	name	count in	note
		Prefabricated units
one	KPSK-270103-С-31-KZHI-KR-1	Frame flat KP1	2
2	KPSK-270103-С-31-КЖИ-С1	Grid C1	four
3		Line items ¯ 8 AI = 280	32	0.11
		Materials B15 concrete	m3	0.41

STEEL CONSUMPTION STATEMENT

MARK ELEMENT	ARMATURE PRODUCTS				TOTAL
	Armature class		Armature class
	ASH		AI
	GOST 5781 - 82		GOST 5781 -82
	¯25	Total	eight	Total
K - 1	68.96	68.96	10.78	10.78	79.74

¯25 = 17,24-2-2 = 68,96

¯8 = 9 0.11 -2 + 12 -0.11 -4 + 32 -0.11 = 10.78

Check: 35.47 -2 + 1.32 -4 + 32 -0.11 = 79.7

Type 3 task.

Given:

Ndl = 1000kN

Ncr = 1500kN

l0 = 6.4m

concrete B15, Indirect (local) reinforcement. Calculation example bi = 0.85

fittings AIII

Find b = h; Asc.

Decision.

1) find in the printout:

Rb = 8.5 Indirect (local) reinforcement. Calculation example 0.85 = 7.23mPa

Rs = 365 mPa

2) Set by j = 1 and m = 1% = 0.01;

3) determine the N = Ndl + Ncr

N = 1000 + 1500 = 2500 kN

4) Find

A = N / j • (Rb + m • Rsc) = 2500 • 103 / (7.23 + 0.01 • 365) (100) =

1363cm2

b = h = Indirect (local) reinforcement. Calculation example = 37cm; taking into account the unification round to 40cm. A = 40 • 40 = 1600cm2

5) We find Ndl / N = 1000/2500 = 0.4; l = l0 / h = 640/40 = 16

6) According to table 8, interpolating, we find jzh = 0.86, jc = 0.82

7) according to the formula 2 we define j = jв + 2 (jj-jв) • a £ jж

j = jb + 2 (jl-jb) • Rsc • Asc) / Rb • A. Replacing Asc / A = 0.01, we get:

j = 0.82 + 2 (0.86-0.82) • 365 / 7.23 • 0.01 = 0.88 ›0.86, successively, we take j = 0.86

8) According to the formula (4) we find:

Asc = N / j • Rss-A • Rb / Rsc = 2500 • 103 / 0.86 • 365 (100) -1600 • 7.23 / 365 = 15.2 cm2

9) Determine the% reinforcement: m = 15.2 / 1600 • 100 = 1%

Finally, we take a column with a cross section of 40 • 40 cm with a longitudinal working reinforcement 4¯22 AIII with Asc. Fact = 15.2 cm2 (see table 7 of the annex).

The transverse rods taken from the welding conditions in table 3 of the application

dw = 8АI with step Sw = 20d = 20 • 22 = 440mm

Table 1

Calculated resistance concrete for limiting states the first groups Rb and Rbt mPa in dependencies from class concrete by strength on compression

Kind of resistance	Concrete					Concrete compressive strength class
						B12.5			B15					IN 20		B 25			VZO				B 35			B40
Compression oseeoe (prismatic strength) Rb	Heavy had a grained					7.5			8.5					11.5		14.5			17				19.5			22
Axial stretch Rbt	Heavy					0.6			0.75					0.9		1.05			1.2				1.3			1.4
table 2

			Estimated reinforcement resistances for group I of limit states Rs, MPa
			Stretched																		Compressed rsc
Type and grade of steel;			longitudinal, transverse (clamps and limb) for bending on an inclined section. Rs								transverse (clamps and bends) in the calculation of the transverse force Rsw

Hot rolled round grade A- I			225								175										225							: '
Hot rolled periodic
class profile: A-ll			280								225										280
A-III d-8 mm			355								285										355
A-III d- 10. ..40 mm \|			365								290										365
Wire reinforcing periodic profile class bp-i											.
d, mm:
3			375								270										375
four			370								265										365
five			360								260										360
table 3 The ratio between the diameters of the welded rods
The diameters of the rods in one direction d1 (mm)		3		four	five		6	eight		ten		12	14		sixteen		18	20		22		25		28	32		36		40
The smallest allowable diameters of rods in a different direction d2 (mm)		3		3	3		3	3		3		four	five		five		6	6		eight		eight		ten	ten		12		12

table 4

The modulus of elasticity of reinforcing steel Es

Type and grade of steel	The modulus of elasticity of reinforcement Es.MPa
Core steel AI and A-II	210,000
A-IIIb	200,000
A-IV, A-VI, AT-IIIC	190,000
Reinforcing Wire B-II, BP-II, BP-I	200,000 170,000
Reinforcement ropes K-7, K-19	180,000

table 5

Table: Values 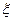Indirect (local) reinforcement. Calculation example at IOAMAH

Reinforcement class	Coefficient
		IN 20	VZO	B40	B50	B60
AI	at	0.65	0.59	0.55	-	-
AI	AOmax	0.48	0.42	0.4	-	-
AP	at	0.62	0.57	0.52	0.47	0.44
AP	AOmax	0.43	0.41	0.38	0.36	0.34
A-III with ¯ 6-8 mm	at	0.59	0.54	0.5	0.44	0.41
A-III with ¯ 6-8 mm	AOmax	0.42	0.39	0.37	0.34	0.33

table 6

Coefficient values 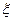Indirect (local) reinforcement. Calculation example AO,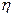

		AO			AO
0.41	0.795	0.326	0.57	0.715	0.408
0.42	0.79	0.332	0.58	0.71	0.412
-	-	-	0.59	0.705	0.416
0.43	0.785	0.337	0.6	0.7	0.42
0.44	0.78	0.343
0.45	0.775	0.349	0.61	0.695	0.424
0.46	0.77	0.354	0.62	0,69	0.428
0.47	0.765	0.359	0.63	0.685	0.432
0.48	0.76	0.365	0.64	0.68	0.435
			0.65	0.675	0.439
0.49	0.755	0.37	0.66	0.672	0.442
0.5	0.75	0.375
0.51	0.745	0.38	0.67	0.665	0.446
0.52	0.74	0.385	0.68	0.66	0.449
0.53	0.735	0.39	0,69	0.655	0.452
0.54	0.73	0.394	0.7	0.65	0.455
0.55	0.725	0.399	_	-	-
0.56	0.72	0.403	-	-	-
0.01	0.995	0.01	0.21	0.895	0.188
0.02	0.99	0.02	0.22	0.89	0.196
0.03	0.985	0.03	0.23	0.885	0.203
0.04	0.98	0.039	0.24	0.88	0.211
0.05	0.975	0.048
0.06	0.97	0.058	0.25	0.875	0.219
			0.26	0.87	0,226
0.07	0.965	0.067	0.27	0.865	0.236
0.08	0.96	0.077	0.28	0.86	0.241
0.09	0.955	0.085	0.29	0.855	0.248
0.1	0.95	0.095	0.3	0.85	0.255
0.11	0.945	0,104	-	-	-
0.12	0.94	0.113	0.31	0.845	0,262
			0.32	0.84	0.269
0.13	0.935	0.121	0.33	0.835	0.275
0.14	0.93	0.13	0.34	0.83	0.282
0.15	0.925	0.13	0.35	0.825	0,289
0.16	0.92	0.147	0.36	0.82	0,295
0.17	0.915	0.155	-	-	-
0.18	0.91	0.164	0.37	0.815	0.301
0.19	0.905	0.172	0.39	0.805	0.314
0.2	0.9	0.18	0.4	0.8	0.32

table 7

Cross-sectional areas and mass of reinforcement bars

d			square and cross		sections	(sm.kv.) with the number of rods				weight 1 m	d
mm	one	2	3	four	five	6	7	eight	9	kg	mm
3	0.071	0.14	0.21	0.28	0.35	0.42	0.49	0.57	0.64	0.055	3
four	0.126	0.25	0.38	0.50	0.63	0.76	0.88	1.01	1.13	0.098	four
five	0.196	0.39	0.59	0.79	0.98	1.18	1.37	1.57	1.77	0.154	five
6	0.283	0.57	0.85	1.13	1.42	1.70	1.98	2.26	2.55	0.222	6
7	0.385	0.77	1.15	1.54	1.92	2.31	2.69	3.08	3.46	0.302	7
eight	0.503	1.01	1.51	2.01	2.51	3.02	3.52	4.02	4.53	0.395	eight
9	0.636	1.27	1.91	2.54	3.18	3.82	4.45	5.09	5.72	0.499	9
ten	0.785	1.57	2.36	3.14	3.93	4.71	5.50	6.28	7.07	0.617	ten
12	1,510	2.26	3.39	4.52	5.65	6.79	7.92	9.05	10.18	0.888	12
14	1.539	3.08	4.62	6.16	7,69	9.23	10.77	12.31	13.85	1,208	14
sixteen	2,011	4.02	6.03	8.04	10.05	12.06	14.07	16.08	18.10	1.578	sixteen
18	2.545	5.09	7.63	10.18	12.72	15.27	17.81	20.36	22.90	1,993	18
20	3.142	6.28	9.41	12.56	15.71	18.85	21.99	25.14	28.28	2.466	20
22	3,801	7.60	11.40	15.20	19.00	22.81	26.61	30.41	34.21	2,994	22
25	4,909	9.82	14.73	19.63	24.54	29.45	34.36	39.27	44.18	3,853	25
28	6.158	12.32	18.47	24.63	30.79	36.95	43.10	49.26	55.42	4.83	28
32	8,043	16.08	24.13	32.17	40.21	48.25	56.30	64.34	72.38	6.313	32
36	10.18	20.36	30,54	40.72	50.9	61.08	71.26	81.44	91.62	7.99	36
40	12.56	25.12	37.68	50.24	62,8	75.36	87.92	100.48	113.04	9.87	40

table 8

The values of the coefficients jж and jв

Ndl	jж and jв at l0 / h
N	6	eight	ten	12	14	sixteen	18	20
jq factor
0	0.93	0.92	0.91	0.9	0.89	0.86	0.83	0.8
0.5	0.92	0.91	0.9	0.88	0.85	0.8	0.73	0.65
one	0.92	0.91	0.89	0.86	0.81	0.74	0.63	0.55
jj coefficient
0	0.93	0.92	0.91	0.9	0.89	0.87	0.84	0.81
0.5	0.92	0.92	0.91	0.9	0.87	0.84	0.8	0.75
one	0.92	0.91	0.9	0.88	0.86	0.83	0.77	0.7

Note: Ndl - the longitudinal force from the action of constant and prolonged loads;

Ncr - longitudinal force from the action of all loads (constant, long-term, short-term)
Questions for self-control

on the topic: "The calculation of compressed elements with random eccentricities ."

1. What are the three types of compressed elements, depending on the characteristics of their reinforcement?

2. How is the cross-section and characteristics of materials of compressed elements prescribed for random eccentricities?

3. What is random eccentricity and what is it equal to?

4. What are the design features of compressed elements with eccentricities more random?

5. What are the two main cases of destruction of compressed elements with eccentricities more than random?

6. What is the condition that determines each of the two cases of a compressed element?

7. What is the main strength condition of a compressed element and how is the height of a compressed zone determined?

8. How is the influence of deflection in flexible compressed elements taken into account?

9. What is the course of the calculation of compressed elements with eccentricities more random (separately for each of the three types of characteristic practical problems).

10. Name the types of valves according to the nature of work.

11. Name the types of reinforcement by type of surface.

12. How is the diameter and pitch of the transverse rods in the frame of the column.

13. Name the definitions of the coefficients j and l.

14. What is Ndl and Ncr?

15. What is indirect reinforcement mesh; how is their calculation made?

16. What are flexible and rigid reinforcement and structural requirements for the reinforcement of columns.

CALCULATION OF COLUMNS (TYPE I ) Check N < Nce h .

N dl (kN)	N cr (kN)	l 0 (m)	b = h (cm)	vi	Concrete	Fittings
1000	500	6.4	40	0.85	20	8¯18 AII
1300	600	5.8	35	0.9	thirty	8¯20 AII
1500	900	6.2	thirty	0.85	20	8¯22 AII
1100	400	5.4	45	0.95	0 ^	8¯20 AIII
900	700	6.0	40	one	20	8¯18 All
1700	800	6.4	50	one	25	8¯20 AIII
1200	500	5.7	43	0.9	thirty	4¯25 AIII
1400	600	6.1	32	0.85	20	8¯20 AIII
1200	400	5.2	35	0.9	15	4¯20 AIII
1000	500	6.4	45	one	25	4¯22 All
1200	700	5.8	50	0.85	thirty	418 AIII
1500	400	6.2	35	0.9	15	4¯20 All
1100	600	6.4	40	one	25	4¯22 All
1400	500	6.0	35	one	20	4¯18 ASH
1300	400	5.2	40	one	thirty	4¯20 AIII
1100	600	6.2	35	one	thirty	4¯20 AIII
1000	500	6.2	45	one	thirty	4¯20 All
1400	400	5.4	45	0.9	20	4¯20 All
1200	400	5.8	35	0.9	20	8¯22 All
1300	600	5.6	40	0.85	25	8¯22 AIII
1200	500	5.2	40	one	25	8¯18 All
900	400	6.4	40	0.85	thirty	8¯20 All
1100	500	6.2	45	0.9	15	8¯20 AIII
1500	400	6.0	40	0.9	20	8¯20 All
1000	600	5.2	35	one	thirty	8¯18 AIII

Calculation of columns Type 2.

	N dl (kN)	N cr (kN)	l 0 (m)	b = h. ( cm )	vi	Concrete	Armat.
one	600	600	4.2	thirty	one	20	111
2	700	600	4.5	thirty	0.85	15	111
3	1000	500	5.2	45	0.8	15	111
four	900	500	4.8	35	one	15	eleven
five	800	1000	5.9	31	one	15	111
6	1100	900	5.4	37	0.8	thirty	111
7	1300	1000	4.9	39	one	20	eleven
eight	1600	800	6.0	42	0.9	25	eleven
9	900	1200	6.8	50	0.95	15	eleven
ten	1000	1500	6.5	41	one	25	111
eleven	800	600	4.3	thirty	one	25	eleven
12	1400	1300	6.2	52	0.85	20	111
13	500	1100	5.3	44	0.9	15	111	As =? -
14	1000	900	6.4	40	one	20	eleven
15	1400	1200	6.1	43	0.8	thirty	eleven
sixteen	700	300	4.0	33	one	15	111
17	400	700	5.0	25	one	25	111
18	1000	300	5.8	29	0.85	25	eleven
nineteen	700	700	3.9	28	0.95	thirty	111
20	900	1200	8.0	40	0.9	15	111
21	1200	1200	7.7	45	one	20	eleven
22	400	500	6.3	35	0.8	15	111
23	900	1100	7.0	37	one	25	eleven
24	1900	1700	8.7	48	0.9	thirty	eleven
25	1700	1000	7.2	45	one	20	111

Calculation of columns. Type 3.

	N dl (kN)	N cr (kN)	l 0 (m)	in i	Concrete	Ar - ra	b =? h =? As =?
one	950	1050	7.2	one	15	II
2	1200	800	5.2	one	25	III
3	900	1000	6D	one	20	II
four	1150	850	5.5	one	25	III
five	1000	850	6.0	0.8	thirty	II
6	1300	1000	4.8	0.8	thirty	III
7	1400	1100	4.3	0.85	25	II
eight	700	400	4.5	0.8	20	III
9	900	1200	7.3	0.9	25	II
ten	1500	900	6.5	0.8	20	III
eleven	800	1000	4.7	0.9	20	II
12	1200	750	4.6	0.9	25	III
13	800	500	4.3	one	15	II
14	1000	700	5.6	0.9	20	III
15	1200	1000	4.2	0.85	25	II
sixteen	1300	900	6.1	0.9	20	III
17	1100	850	5.7	one	25	II
18	900	500	4.5	0.9	15	III
nineteen	1200	900	5.1	0.85	25	II
20	900	1350	5.3	1h	20	III
21	1000	1500	6.2	0.9	25	II
22	800	450	4.9	one	15	III
23	900	1250	5.8	0.85	thirty	II
24	1100	750	4.2	0.9	15	III
25	700	900	4.0	one	15	II

Что бы оставить комментарий войдите

Комментарии (0)

Indirect (local) reinforcement. Calculation example

Building construction