In geodesy, it is often necessary to transfer coordinates from one point to another. For example, knowing the source coordinates of point A (Fig. 23), the horizontal distance of the SAB from it to point B, and the direction of the line connecting both points (directional angle αAB or rumb ), you can determine the coordinates of point B. In this formulation, the transfer of coordinates is called a direct geodetic problem .
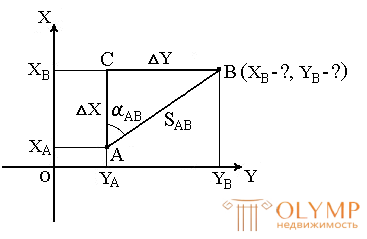
Fig. 23. Direct geodetic task
For points located on a spheroid, the solution to this problem presents considerable difficulties. For points on a plane, it is solved as follows.
Given: Point A (XA, YA) , SAB and αAB .
Find: point B (XB, YB) .
Directly from the figure we have:
ΔX = XB - XA ;
ΔY = YB - YA .
Differences ΔX and ΔY coordinates of points subsequent and previous points are called increments of coordinates. They are projections of the segment AB on the corresponding coordinate axes. We find their values from the rectangular rectangle ABC :
ΔX = SAB · cos αAB ;
ΔY = SAB · sin αAB .
Since in these formulas SAB is always a positive number, the signs of the increments of the coordinates ΔX and ΔY depend on the signs cos αAB and sin αAB . For various angles, the signs ΔX and ΔY are presented in Table 1.
Table 1.
The signs of the increments of coordinates ΔX and ΔY
| Coordinate increments | A quarter of the circle in which the line is directed | |||
| I (CB) | II (SE) | III (SW) | IV (NW) | |
| ΔX | + | - | - | + |
| ΔY | + | + | - | - |
With the help of rumba, the increments of coordinates are calculated by the formulas:
ΔX = SAB · cos rAB ;
ΔY = SAB · sin rAB .
Signs increments are given depending on the name of the rumba.
Having calculated the increments of coordinates, we find the desired coordinates of another point:
XB = XA + ΔX ;
YB = YA + ΔY .
Thus, it is possible to find the coordinates of any number of points by the rule: the coordinates of the next point are equal to the coordinates of the previous point plus the corresponding increments.
The inverse geodesic problem is that given the known coordinates of the points A (XA, YA) and B (XB, YB), it is necessary to find the length SAB and the direction of the line AB : rumb and rAB and the direction angle αAB ( Fig.24 ).
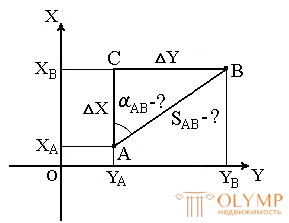
Fig. 24. Inverse geodetic problem
This problem is solved as follows.
First we find the increments of the coordinates:
ΔX = XB - XA ;
ΔY = YB - YA .
The angle rAB is determined from the relation
|
ΔY |
= tg rAB |
|
ΔX |
.
The signs of the coordinate increments calculate the quarter in which the point is located, and its name. Using the relationship between directional angles and points, we find αAB .
To control the distance SAB is calculated twice by the formulas:
| SAB = | ΔX | = | ΔY |
= ΔX · sec αAB = ΔY · cosec αAB |
| cos αAB | sin αAB |
| SAB = | ΔX | = | ΔY |
= ΔX · sec rAB = ΔY · cosec rAB |
| cos rAB | sin rAB |
SAB distance can also be determined by the formula
.
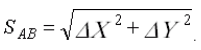
Что бы оставить комментарий войдите
Комментарии (0)