2.3 Прямая и обратная геодезические задачи сущность и применение кратко

Прямая геодезическая задача и обратная геодезическая задача - это две основные задачи в геодезии, которые связаны с определением координат точек на земной поверхности.

Прямая геодезическая задача заключается в определении координат точки B на земной поверхности на основе известных координат точки A и расстояния между точками A и B. В этой задаче мы ищем точку B на земной поверхности, зная ее расстояние от точки А и координаты точки А. Для решения этой задачи используются различные методы и инструменты, включая триангуляцию, тахеометрию, геодезические приборы и глобальную навигационную спутниковую систему (ГНСС).

Обратная геодезическая задача заключается в определении расстояния и направления между двумя точками на земной поверхности на основе известных координат этих точек. В этой задаче мы ищем расстояние и направление между точками А и B на земной поверхности, зная их координаты. Для решения этой задачи используются формулы и алгоритмы, основанные на геодезической теории и математической геодезии. Важной составляющей решения обратной геодезической задачи является учет эллиптической формы Земли и ее геодезических параметров, таких как большая полуось, малая полуось и измеренная сфероидальность.

Обе эти задачи являются важными для геодезических измерений и картографии, а также для различных областей, таких как геоинформатика, строительство, транспорт и многие другие.

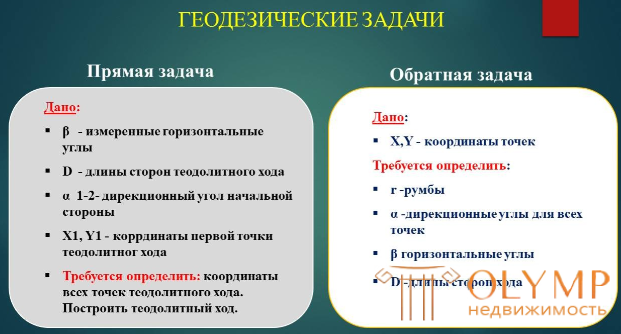
Геодезическая задача — математическая задача, связанная с определением взаимного положения точек (координат) принадлежащих какой-либо поверхности. Геодезические задачи подразделяются на прямую, обратную и задачу Потенота.

2.3.1. Прямая геодезическая задача

В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние SAB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол αAB или румб rAB), можно определить координаты точкиВ. В такой постановке передача координат называется прямой геодезической задачей.

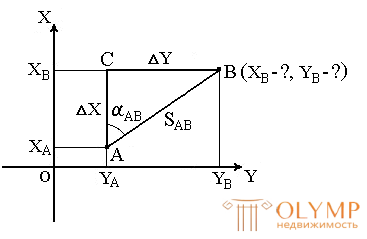
Рис. 23. Прямая геодезическая задача

Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.

Дано: Точка А( X_A, Y_A ), S_AB и α_AB.

Найти: точку В( X_B, Y_B ).

Непосредственно из рисунка имеем:

ΔX = X_B – X_A ;

ΔY = Y_B – Y_A .

Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:

ΔX = S_AB · cos α_AB ;

ΔY = S_AB · sin α_AB .

Так как в этих формулах S_AB всегда число положительное, то знаки приращений координат ΔX и ΔY зависят от знаков cos α_AB и sin α_AB. Для различных значений углов знаки ΔX и ΔY представлены в табл.1.

Таблица 1.

Знаки приращений координат ΔX и ΔY

Приращения координат	Четверть окружности в которую направлена линия
	I (СВ)	II (ЮВ)	III (ЮЗ)	IV (СЗ)
ΔX	+	–	–	+
ΔY	+	+	–	–

При помощи румба приращения координат вычисляют по формулам:

ΔX = S_AB · cos r_AB ;

ΔY = S_AB · sin r_AB .

Знаки приращениям дают в зависимости от названия румба.

Вычислив приращения координат, находим искомые координаты другой точки:

X_B = X_A + ΔX ;

Y_B = Y_A + ΔY .

Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.

2.3.2. Обратная геодезическая задача

Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румб r_AB и дирекционный угол α_AB (рис.24).

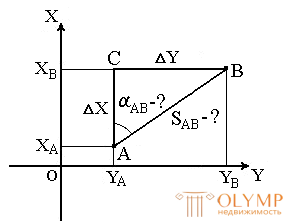
Рис. 24. Обратная геодезическая задача

Даннная задача решается следующим образом.

Сначала находим приращения координат:

ΔX = X_B – X_A ;

ΔY = Y_B – Y_A .

Величину угла r_AB определем из отношения

ΔY/ΔX = tg r_AB

.

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название.

Используя зависимость между дирекционными углами и румбами, находим α_AB.

Для контроля расстояние S_AB дважды вычисляют по формулам:

Расстояние S_AB можно определить также по формуле

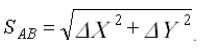
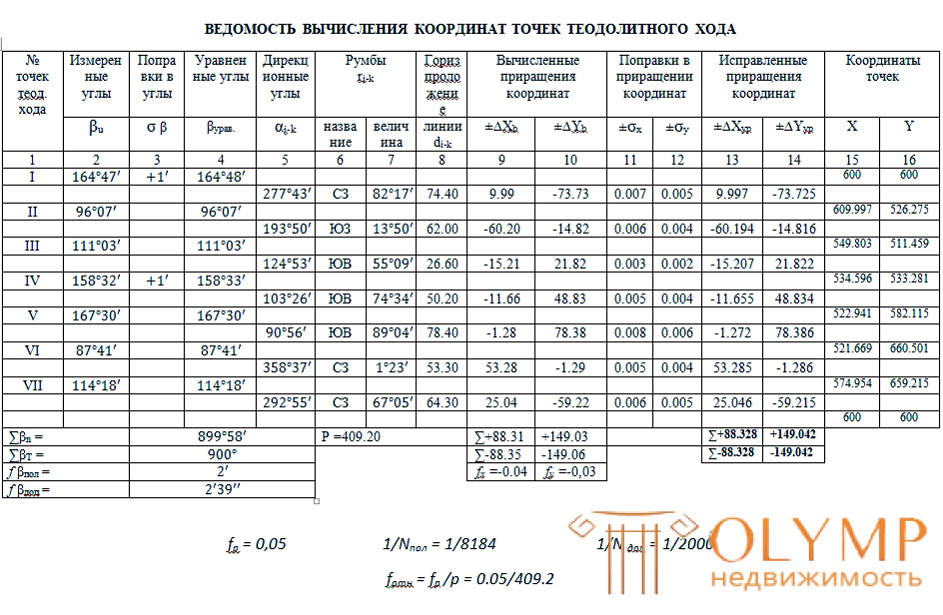
Пример применения задач для заполнения ведомости координат точек теодолитного хода

Задача Потенота

Задача Потенота (обратная геодезическая засечка) — одна из классических математических задач определения местоположения точки на местности по трём ориентирам с известными координатами; возникает, например, при определении местоположения корабля в море по трём маякам, расстояние до которых неизвестно. Имеет более 100 аналитических и графических способов решения и является частным случаем более общей задачи трилатерации. Приобрела важное практическое значение в самых разных областях (геодезии, навигации, корректировке ракетно-артиллерийского огня) и не потеряла актуальности по настоящее время.

Формулировка задачи Потенота

Найти точку плоскости, из которой стороны данного (плоского) треугольника видны под заданными углами.

Замечание. Если все эти углы равны между собой и равны 120 градусам, то искомая точка есть Точка Торричелли.

Сущность обратной засечки состоит в определении координат четвертого пункта по координатам трёх исходных и двум измеренным углам при определяемом пункте.

Для решения этой задачи известно много формул. Здесь приводятся формулы Кнейссля, как наиболее экономичные для решения на микрокалькуляторах.

Решение задачи по формулам Кнейссля.

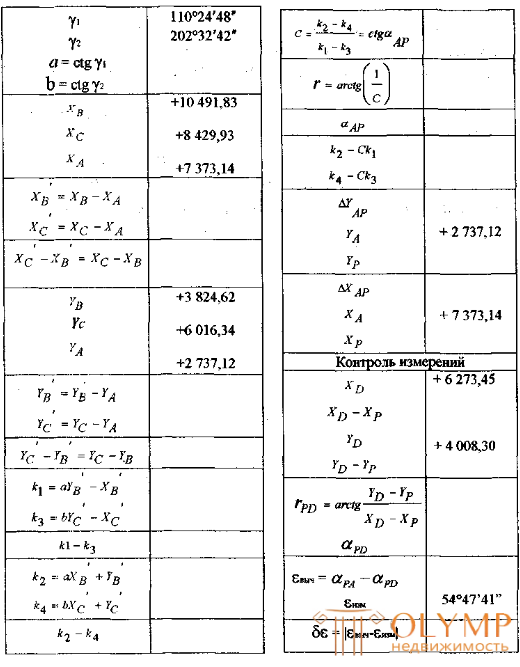
По координатам трёх исходных пунктов А, В, С и двум измеренным углам γ₁ γ₂- (рис.-4) вычислить координаты пункта Р и произвести контроль определения координат по измеренному углу s между направлениями на пункт А и четвертый исходный пункт D.

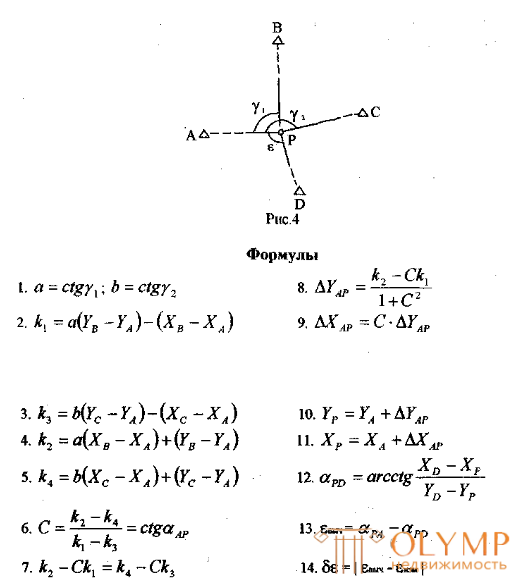
Порядок решения.

1 .Находят а = ctg γ₁ и b = ctg γ₂ с шестью десятичными знаками.

2.Вычисляют разности координат исходных пунктов, входящие в формулы (2),(3),(4) и (5 ). Последние строки для разностей Х-ов и Y-ов в схеме являются контрольными.

3 .По формулам (2),(3 ),(4),(5 ) вычисляют значения k₁, k₂, k₃, k₄ , а затем величину С по формуле (6). Контролируют вычисления по формуле (7 ).

4. По формулам (8) и (9) вычисляют приращения координат ΔY_AР и ΔX_AР.

Затем находят координаты X _р, Y_p по формулам (10) и (11).

5.По формулам (12), (13) и (14) производят контроль измерений. Значение δε не должно превышать 1’.

Применение Прямой и обратной геодезических задач

Прямая и обратная геодезические задачи используются для определения точных координат и расстояний между точками на земной поверхности. Это имеет множество приложений в различных областях, включая:

1. Картография: прямая и обратная геодезические задачи позволяют определить координаты точек на земной поверхности и создавать точные карты и географические информационные системы.

2. Строительство: геодезические измерения используются для создания проектов и строительства зданий, мостов, дорог и других инженерных сооружений.

3. Транспорт: геодезические измерения используются для планирования маршрутов транспорта и управления транспортными потоками.

4. Геология и геофизика: прямая и обратная геодезические задачи используются для измерения геологических и геофизических параметров, таких как расстояния между пластами и глубина залегания рудных месторождений.

5. Экология и охрана окружающей среды: геодезические измерения используются для мониторинга и анализа изменений в окружающей среде, например, для измерения уровня загрязнения воды или земли.

6. Геоинформатика: прямая и обратная геодезические задачи используются в геоинформационных системах для обработки, анализа и визуализации геоданных.

Это лишь несколько примеров, как прямая и обратная геодезические задачи используются в различных областях, и их приложения могут быть очень разнообразными.