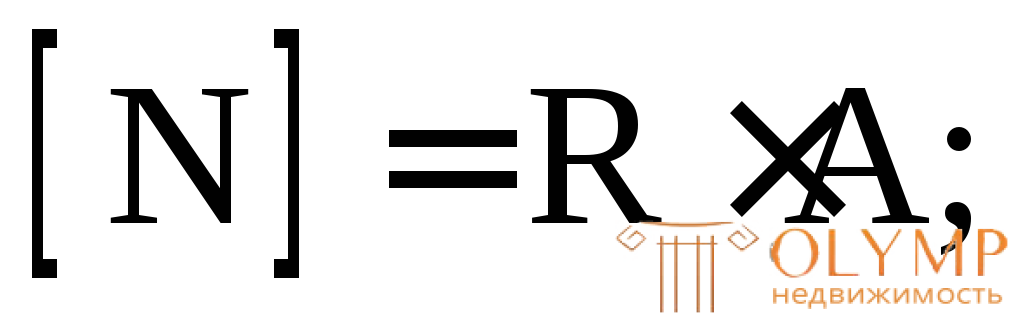
Определение напряжений и расчеты на прочность при центральном растяжении–сжатии кратко

При центральном растяжении-сжатии нормальные напряжения в поперечных сечениях, достаточно удаленных от места приложения сил, постоянны (принцип Сен-Венана) и определяются по формуле:

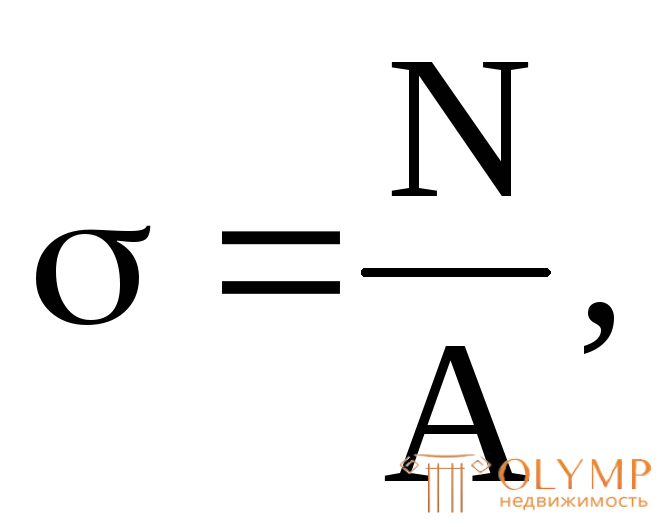Определение напряжений и расчеты на прочность при центральном растяжении–сжатии (3.1)

+где Определение напряжений и расчеты на прочность при центральном растяжении–сжатии – нормальное напряжение; А – "чистая" площадь поперечного сечения бруса после вычета возможных ослаблений сечения отверстиями, т.е. А = А_netto.

Если площадь поперечного сечения бруса постоянна по длине, то условие прочности для пластичного материала имеет вид (при условии, что коэффициенты условий работы и надежности равны единице, т.е. γ = 1, γ_н= 1):

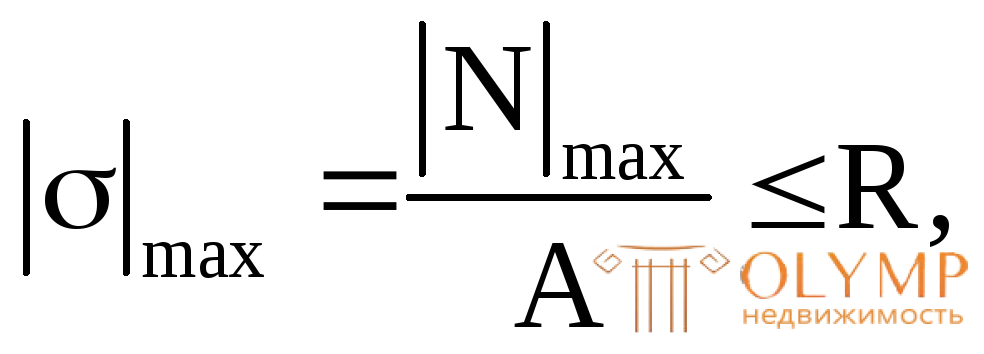N Определение напряжений и расчеты на прочность при центральном растяжении–сжатии ARили(3.2)

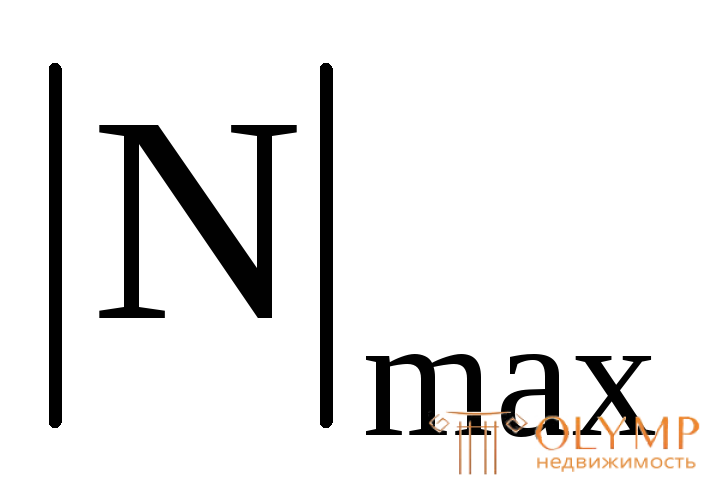где Определение напряжений и расчеты на прочность при центральном растяжении–сжатии – наибольшее значение продольной силы по абсолютной величине берется из эпюры N (сечение, где имеется 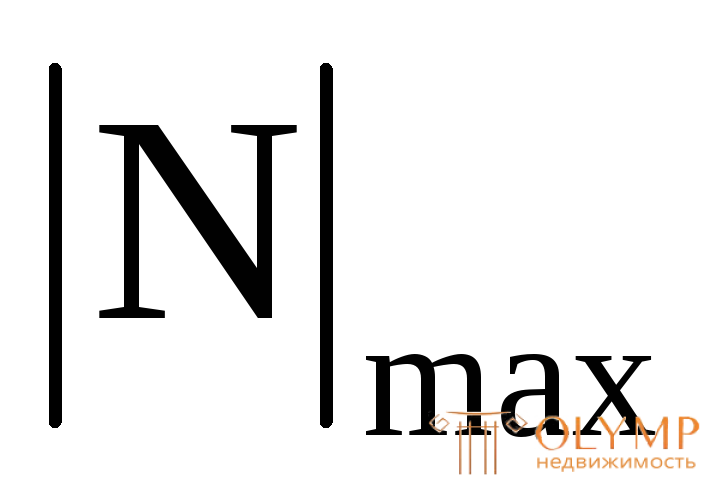Определение напряжений и расчеты на прочность при центральном растяжении–сжатии , является опасным);R– расчетное сопротивление материала по пределу текучести.

Если брус выполнен из хрупкого материала, т.е. когда расчетные сопротивления на растяжение и сжатие различны 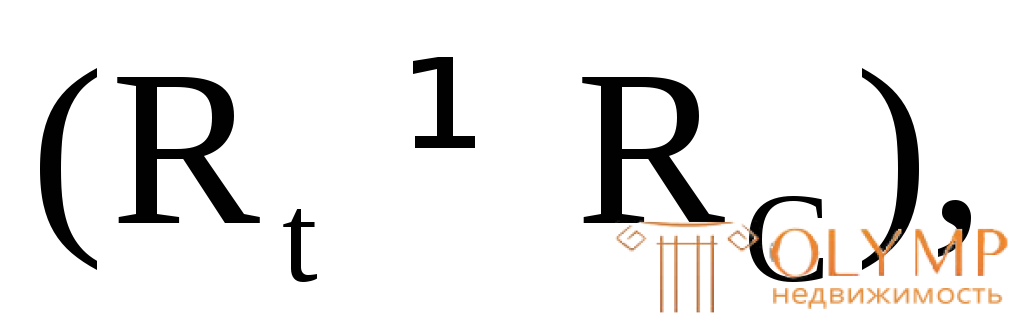Определение напряжений и расчеты на прочность при центральном растяжении–сжатии то условие прочности имеет следующий вид:

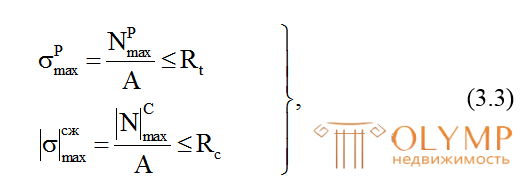
Определение напряжений и расчеты на прочность при центральном растяжении–сжатии

где 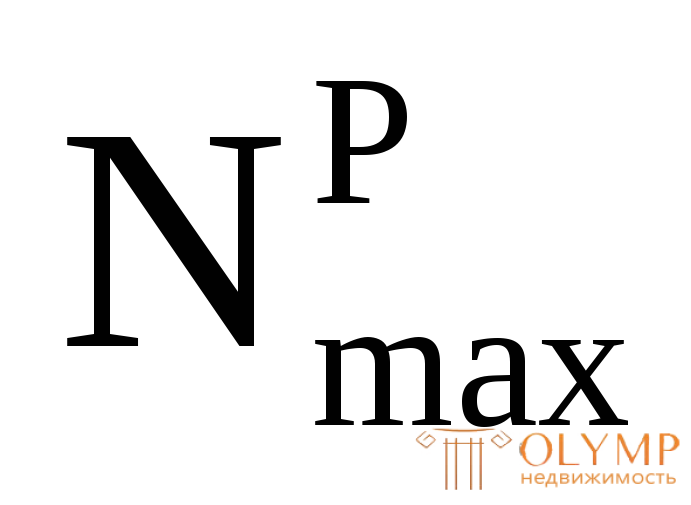Определение напряжений и расчеты на прочность при центральном растяжении–сжатии – наибольшая растягивающая продольная сила (на эпюре N имеет знак "плюс");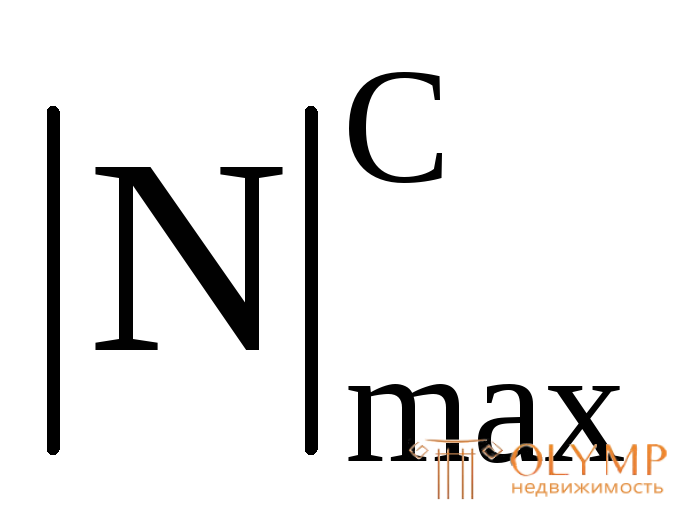– наибольшая по абсолютной величине сжимающая продольная сила (на эпюре N имеет знак "минус"); 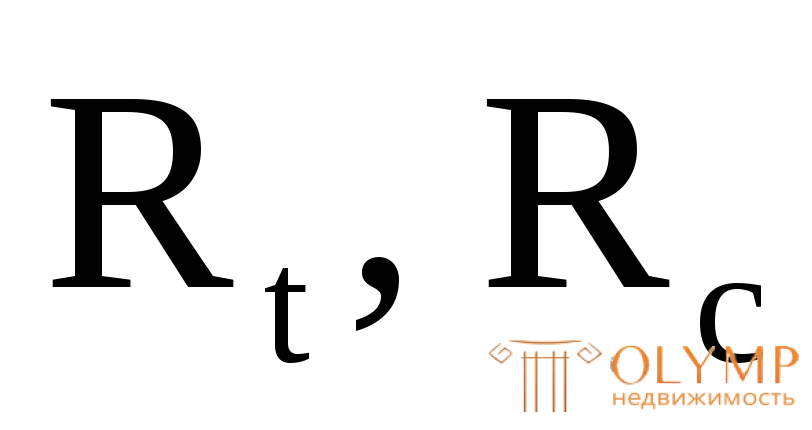Определение напряжений и расчеты на прочность при центральном растяжении–сжатии – расчетные сопротивления материала на растяжение и сжатие по пределу прочности.

Используя условия прочности (3.2) или (3.3), можно решать задачи трех типов:

1-й тип – проверочная задача. Используя все заданные величины и эпюруN, по формулам (3.2) и (3.3) можно проверить прочность бруса.

2-й тип – проектная задача, т.е. подбор сечения бруса.

Приняв 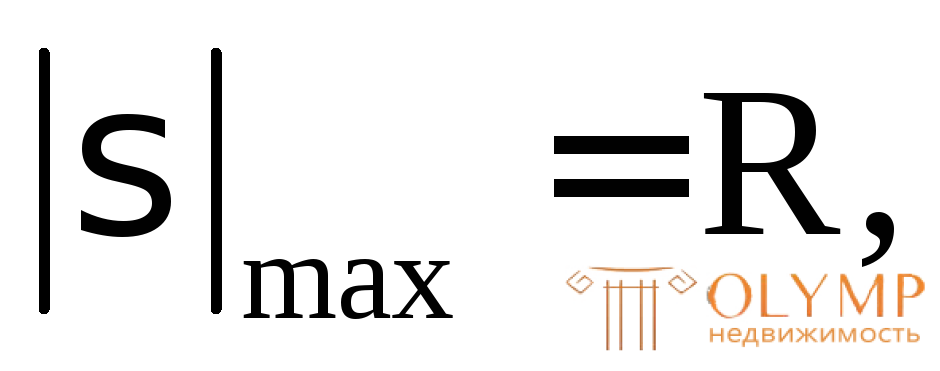Определение напряжений и расчеты на прочность при центральном растяжении–сжатии определяем требуемую для этого величину площадипоперечного сечения из формулы (3.2):

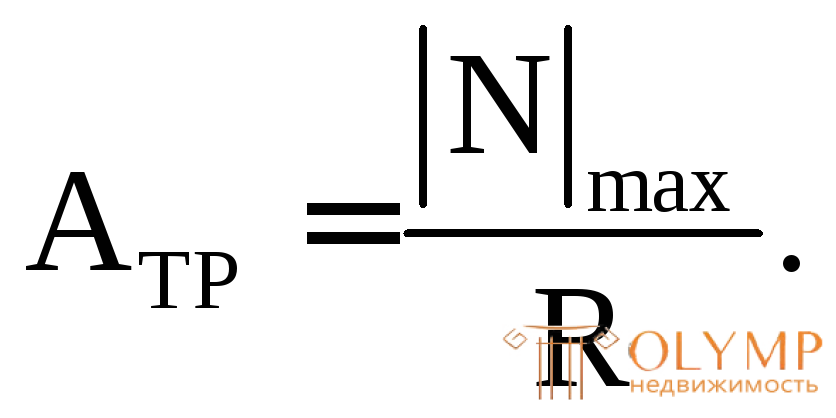Определение напряжений и расчеты на прочность при центральном растяжении–сжатии (3.4)

Зная эту площадь, можно определить конкретные размеры сечения заданной формы.

Для хрупкого материала из формул (3.3) требуемую площадь сечения находим отдельно:

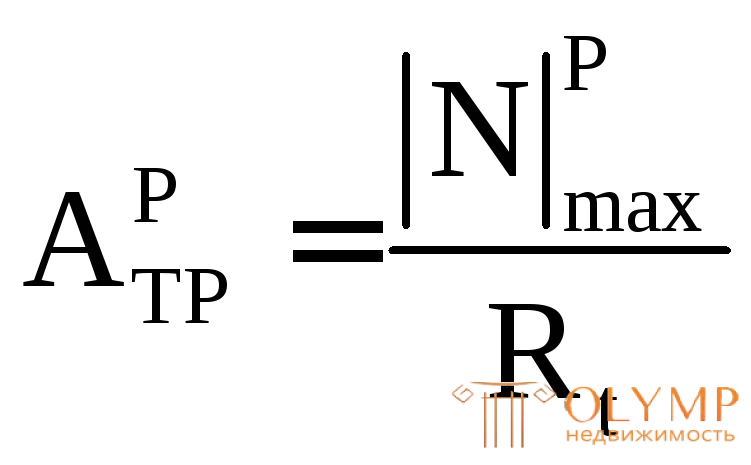
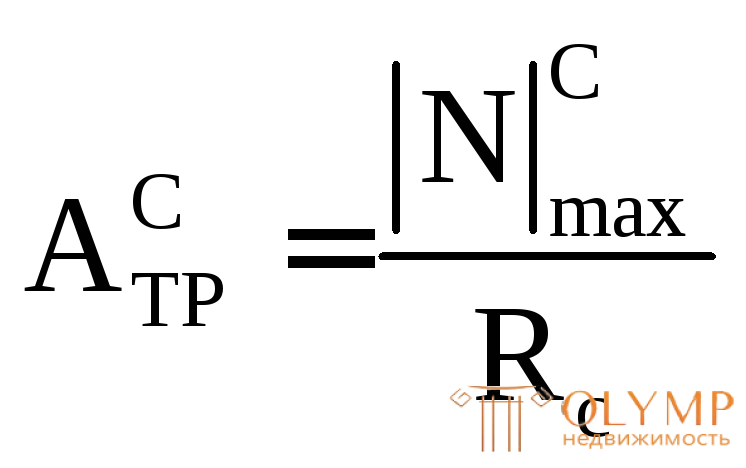для растянутой зоны – Определение напряжений и расчеты на прочность при центральном растяжении–сжатии

и сжатой зоны – Определение напряжений и расчеты на прочность при центральном растяжении–сжатии .

Из полученных значений площадей выбираем большую.

3-й тип – определение несущей способности стержня или определение допускаемой продольной силы.

Приняв 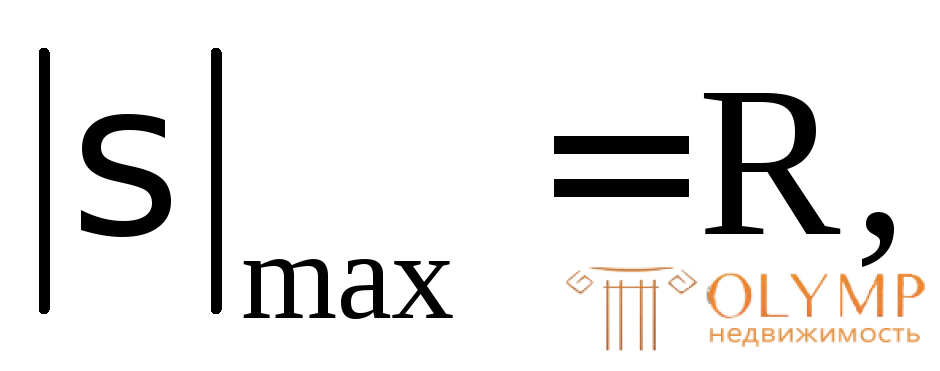Определение напряжений и расчеты на прочность при центральном растяжении–сжатии определяем величину наибольшей допускаемой продольной силы:

– для пластичного материала

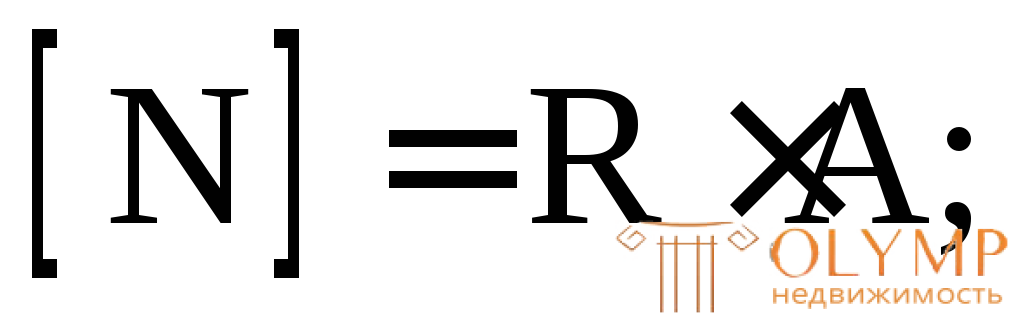Определение напряжений и расчеты на прочность при центральном растяжении–сжатии (3.5)

– для хрупкого материала

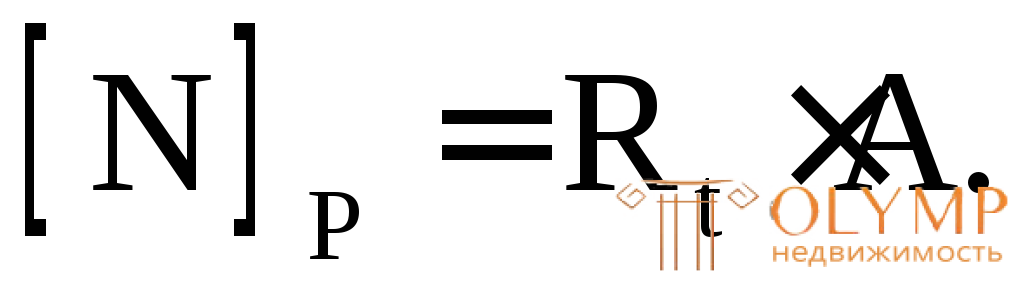
Определение напряжений и расчеты на прочность при центральном растяжении–сжатии

Для бруса из хрупкого материала из двух сил в качестве допускаемой выбираем меньшую:

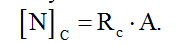
Определение напряжений и расчеты на прочность при центральном растяжении–сжатии

Что бы оставить комментарий войдите

Комментарии (0)

Определение напряжений и расчеты на прочность при центральном растяжении–сжатии кратко

Сопротивление материалов