2.2. Directional angles and axial points, true and magnetic azimuths, the relationship between them

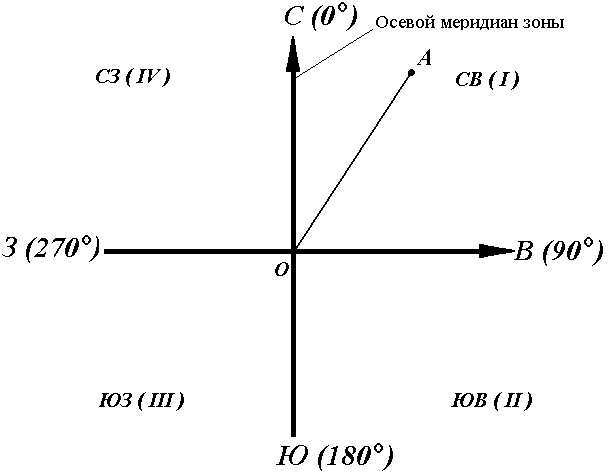
2.2.1. Directional angles and axial points

The axial (middle) true meridian of a zone is often taken as the main direction. In this case, the position of the terrain line relative to the axial meridian determines the orientation angle, called directional (Fig. 16).

The directional angle is measured from the north direction of the axial meridian in a clockwise direction through the east, south and west. Therefore, the degree of the direction angle can be any value from 0 ° to 360 °.

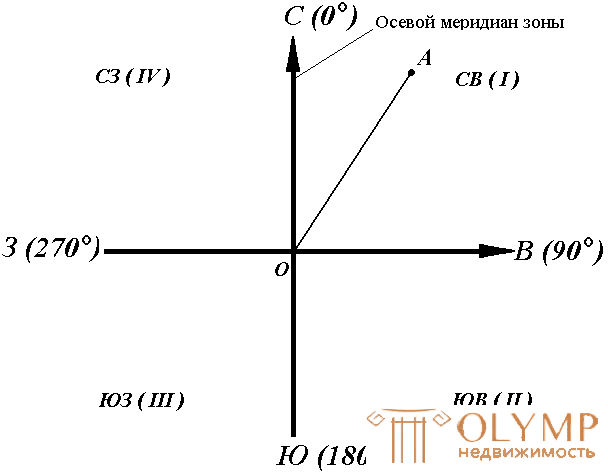
Fig. 16. Directional angles

For the line OA, its directional angle at the point O is the horizontal angle αOA between the north direction of the axial meridian and the direction of the line. For lines ОВ, ОЕ and ОF - α ОВ , α ОE , α ОF .

Thus, the directional angle is the angle in the horizontal plane, measured from the north direction of the axial meridian in the clockwise direction to the given line.

In geodesy, it is customary to distinguish between the forward and reverse direction of the line (Fig. 17). So, if the sun is considered to be the forward direction of the line, then the NE will be the opposite direction of the same line. Accordingly, α BC is the right direction angle of the BC line at point M , and the angle α CB is the reverse direction angle of the same line at the same point.

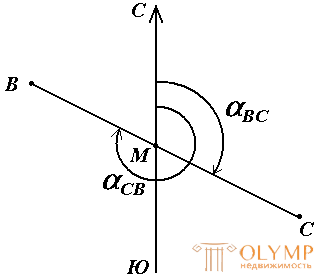
Fig. 17. Forward and reverse line direction

It can be seen from the figure that α CB = α BC + 180 °, i.e. direct and reverse directional angles differ from each other by 180 °.

Sometimes, in order to orientate the terrain line, not the directional angles are used, but the points (Fig. 18).

The axial rhombus is the acute horizontal angle, measured from the nearest direction of the axial meridian (northern or southern) to this line. Rumbas are denoted by the letter r with an index indicating the quarter in which the point is located.

Fig. 18. Rumba and directional corners

The names of the quarters are composed of the corresponding designations of the main points of the horizon: north (C), south (South), east (B), west (B).

The relationship between directional angles and points is determined for quarters by the following formulas:

I quarter (CB) r = α

II quarter (SE) r = 180 ° - α

III quarter (SW) r = α - 180 °

IV quarter (NW) r = 360 ° - α

Rumb at the point M of the direction BC is called direct, and the opposite direction CB - reverse. The forward and reverse points at the same point of this line are equal in numerical value, but have indices of opposite quarters.

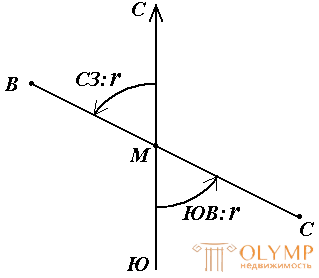
Fig. 19. Forward and reverse rhumba

2.2.2. True azimuths and points

In addition to the axial meridian of the zone, the direction of the true (geographical) meridian can be taken as the main direction when orienting the terrain lines.

The true meridian is the line of intersection of the earth's surface with a plane passing through a plumb line and the axis of rotation of the Earth.

The position of the terrain line relative to the true meridian is determined by the true azimuth or true rumba.

The true azimuth of the line is the angle in the horizontal plane, measured from the northern direction of the true meridian in the clockwise direction to this line (Fig. 20).

The true rumba of the line is a sharp horizontal angle, measured from the nearest direction of the true meridian (north or south) to this line.

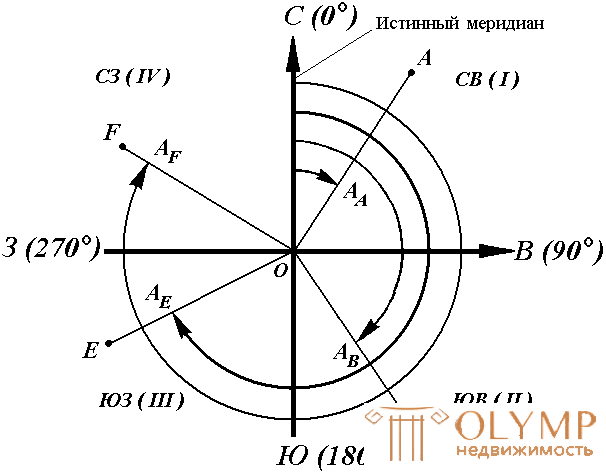
Fig. 20. True azimuths

True azimuth A is measured from 0 ° to 360 °. The relationship between true azimuths and points is the same as that between directional angles and axial points.

True meridians passing through points of the Earth with different longitudes are not parallel with each other and converge at the poles. Therefore, the azimuths of the same straight line, defined relative to different true meridians, differ by the value of γ (Fig. 21), which is called the angle of convergence of the meridians. Its approximate value can be calculated by the formulas:

γ = 0.54 · l · tg φ or γ = sin φ · Δλ,

where l is the length of a straight line between points (km); φ is the average line width; Δλ is the difference in longitude. When l = 1 km and the width of Khabarovsk is φ = 48 ° 28 ', the angle of convergence of the meridians is γ = 0.6' = 36 ".

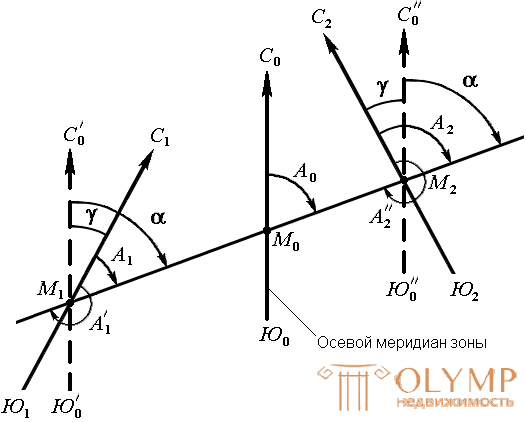
Fig. 21. Dependence between true azimuth and directional angle

To go from a directional angle to the true azimuth and vice versa, it is necessary to know the angle of convergence γ between the axial and true meridians (Fig. 21). The relationship between true azimuth and directional angle is as follows.

A = α + γ.

If the point is located to the west of the axial meridian, then the angle of convergence γ between the axial and true meridian is considered to be negative, while to the east - positive (Fig. 21). For example, the true azimuths of the line at the directional angle α = 70 ° and the approach angle γ = - 0 ° 50 'for the western point M1 , γ = 0 ° 50' for the eastern point - M2 are respectively

A1 = 70 ° - 0 ° 50 '= 69 ° 50',

A2 = 70 ° + 0 ° 50 '= 70 ° 50'.

2.2.3. Magnetic azimuths and points

When orienting the terrain lines, the direction of the magnetic meridian can also be taken as the main direction.

The magnetic needle at the ends has points at which the magnetic masses are concentrated. The line connecting them is called the magnetic axis of the arrow .

The vertical plane passing through the magnetic axis of the arrow is the plane of the magnetic meridian .

The line of intersection of the plane of the magnetic meridian with the horizontal plane gives the direction of the magnetic meridian.

The horizontal angle, measured from the north direction of the magnetic meridian in the clockwise direction to this line, is called the magnetic azimuth Am (Fig. 22).

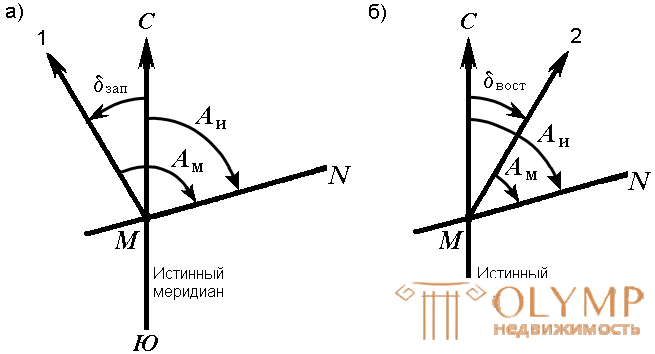
Fig. 22. Magnetic azimuth and magnetic needle declination: a) western; b) eastern

At each point on the surface of the Earth, the magnetic and true meridians form an angle between themselves, called the declination of the magnetic needle δ (Fig. 22). The north end of the magnetic needle may deviate from the true meridian to the west or east. Depending on this, there are western and eastern declinations. Eastern declination is considered to be positive, western - negative:

Au = Am + δ tail ,

Au = Am - δzap .

The magnetic declination at different points on the Earth is different and impermanent. There are secular, annual and daily changes in declination. In this regard, the magnetic needle indicates the direction of the magnetic meridian approximately and the line can be oriented along it only when more precision of orientation is not required.