5. Road rounding

5.1. Circular curves

On all linear structures intended for traffic, in places where the direction of the route changes, in order to pair straight sections in order to smoothly and gradually turn the driving vehicle, curves or curves are made. Curves can be any. The simplest is an arc of a circle of a certain radius, i.e. circular curve.

On railways, circular curves are used with the following radii: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 400 and 300 m. A specific decision on the application of the radii of railway curves is made according to specific conditions and construction technical standards STN Ts-01-95.

The circular curve is characterized by four main points and six main elements (Fig. 8).

The main points of the curve, which determine the position of the curve on the ground, are: the apex of the angle WU; the beginning of the circular curve of the NCC; the middle of the circular curve of the CCM; end of the circular curve of the KKK.

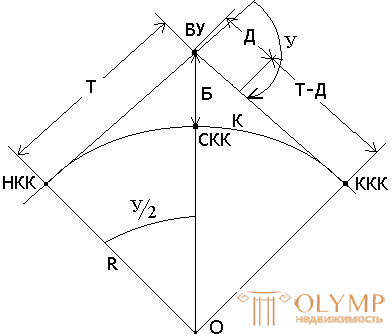
Fig. 8. Diagram of a circular curve.

The main elements of the curve are:

1. The angle of rotation of the highway.

2. Radius R.

During the survey, the angle Y is calculated, and the radius R is assigned. The remaining elements are found by the formulas arising from a right-angled triangle with vertices VU, NKK, O (Fig. 8).

3. The tangent of the curve (tangent) T is the distance in a straight line from the top of the corner to the beginning or end of the curve.

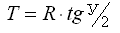
4. The length of the curve K from the beginning of the curve to its end.

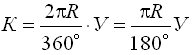
5. The bisector of curve B is a segment from the top of the corner to the middle of the curve.

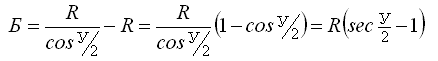
6. Domer D - the difference between the length of two tangents and a curve.

D = 2T - K.

All elements of the curve can be calculated by the above formulas. But since T, K, B and D are directly dependent on the angle of rotation and radius, then special tables for breakdown of curves have been drawn up for their definition.

5.2. Calculating the stationing of the main points of the circular curve

To calculate the stationary values ​​of the main points of the curve means to find out on which pickets and plus points they are.

First, the stationing of the top of the angle of rotation of the vehicle is determined, and then the stationary value of the beginning, end and middle of the curve is found.

.

For control, the stationary value of the end of the curve is calculated again.

QC = WU + T - D.

Example (Fig. 9): Defined: the stationing of the control unit PK1 + 12.48 and the main elements of a circular curve:

Find the picking values ​​of NKK, KKK, SCC. The calculation of the picket of the main points of the curve is performed in the following form:

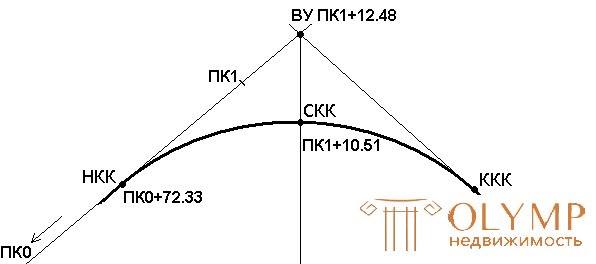
Fig. 9. A breakdown of the picket according to the curve.

5.3. Breakdown of the curve at major points on the ground

Breaking the curve at the main points on the ground means finding the position of its main points on the axis of the linear structure and fixing them. The position of the beginning of the NCC curve is determined by setting the calculated distance from the nearest station.

Fig. 9. A breakdown of the picket according to the curve.

In our example (Fig. 9), the closest picket is PK1. A distance of 27.67 m is laid from it to PK0. At this point a peg is hammered, and at a distance of 15-20 cm in the direction of the route the guards are driven in and the NKK PK0 + 72.33 is recorded on it.

The middle of the CCM curve is fixed, laying off from WU in the direction of the bisector of the angle formed by the directions of the route, a segment equal to B.

At the next, after the top of the corner, the direction of the route is postponed by the value of the domer (see Fig. 8), after which the stationing of the station is continued. At the same time, in the place of deposition of the domer there are two points - the beginning of the domer and its end receive the same picketing name, due to which at the end of the curve the picketing coincides with the straight line picketing. The KKK position is obtained by setting the distance from the end of the domer; in the example, it is 36.21 m. The found position of the KKK is fixed with a peg and a guard.

5.4. Detailed breakdown of the circular curve

It is impossible to accurately construct a curve on the terrain by three main points, therefore during the construction of the route it is designated by a number of additional points. These works are called detailed breakdown of the curve.

The distance between adjacent points on the K curve for a detailed breakdown depends on its radius R and the nature of the structure, but the smaller the R curve, the smaller the K value. at R > 500 m, the breakdown is made at intervals k = 20 m, at 500> R > 100 m k = 10 m, at R <100 m k = 5 m.

Of all the existing methods of detailed breakdown, which differ in the type of measurements and conditions of use, consider two methods.

The method of rectangular coordinates from tangents.

Fig. ten . The method of rectangular coordinates from tangents.

Let M be the beginning of a curve of radius R (Fig.10). We take the tangent of MA for the abscissa axis, and the radius of MO for the ordinate axis. The position of point N, a curve in the adopted coordinate system is determined by the abscissa X1 and the ordinate Y1.

From the ON1 rectangle we find

The angle j is found depending on the length of the arc k , through which the curve is split:

.

Then for points 2, 3, etc. coordinates are calculated by substituting the angles 2 j , 3 j , etc. into the formulas above.

According to the above formulas, tables are compiled, from which, by the arguments of R and k, you can choose the value of X and Y.

In view of the fact that the values ​​of k and X are close to each other, instead of columns X in tables, they often give values ​​( k - X), called “ curve without abscissa ”. The breakdown of the curve produced from two sides - from the beginning and end to the middle of the curve. According to the tangents, the value of k is measured and the value ( k - X) is deposited from the obtained point in the opposite direction. From this point, restore the perpendicular and lay on it the ordinate Y.

The advantage of the method of rectangular coordinates is that each point of the curve is taken out independently of the others with approximately the same accuracy.

A detailed breakdown of the curve by the method of rectangular coordinates is conveniently carried out in open and rugged terrain.

Detailed breakdown of the curve with the help of angles and chords.

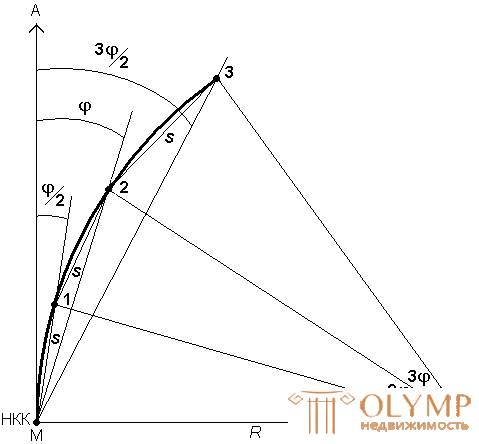
Fig. 11. The method of angles and chords.

This method is based on the fact that the angles with the vertex at any point of the circular curve, formed by a tangent and secant and enclosing equal arcs, are equal to half of the corresponding central angle (Fig. 11).

To split the curve with the help of angles and chords, calculate the central angle j , based on the chord s

.

Calculate the angles j i between the tangent and the direction to the points to be determined.

First, perform a breakdown of the curve from its beginning NKK to the middle of the CCM. For this, the theodolite is set at the beginning of the NCC curve, the zero of the alidade is combined with the zero of the limb and the rotation of the limb directs the sighting axis along the tangent. Then, freeing the alidade, the angle j1 = j / 2 is set aside from the tangent in the direction of the curve and the specified distance s is measured in the direction of the beam of sight. This is how point 1 is found. After that, lay the angle j2 = j , and the tape is transferred and its zero is aligned with point 1. Holding a finger at the division equal to s , rotate the ribbon around point 1 in the direction of the curve until the division hits the beam sightings. Point 2 is marked in this place. Continue to operate in the same sequence, putting off point 3, etc.

Similarly, perform a breakdown of the curve from its end of the KKK to the middle of the CCM.

In the considered method, linear measurements are performed near the curve, which is advantageous when dividing points in cramped conditions, for example, on embankments. But since the position of the next point is obtained relative to the previous one, then with increasing length of the curve, the accuracy of its detailed breakdown rapidly decreases. This is the main drawback of the way corners and chords.

5.5. Carrying pickets on the curve

Since the breakers are moved along the tangents of the curves when the picket is broken down on the highway, it becomes necessary to carry out the pickets located on the tangents on the curves. Pickets delivery to curves is performed using the method of rectangular coordinates and, in principle, does not differ from the detailed breakdown of the curve using this method. The only difference is that with a detailed breakdown of the curve, the necessary data is taken from the tables in which they are given through certain distances along the curve (20, 10, 5, or 1 m). When pickets are removed from the tangent (tangent) to the curve, such data is also found from the tables, but the interpolation method is used.

For example, PC1 lies on the tangent (Fig. 12). In order to make it to the curve, calculate the distance k from PC1 to NKK. It is equal to 27.67 m.

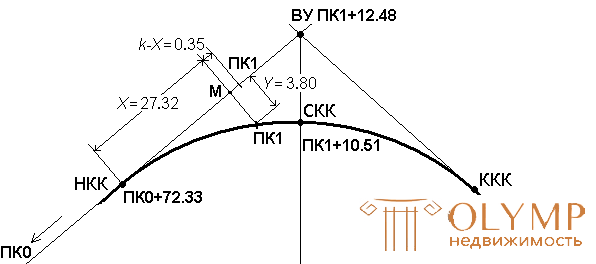
Fig. 12. Transfer of stationing point from tangent to curve.

From the tables at R = 100 m for k = 27.67 m, by interpolation, X = 27.32 m and Y = 3.80 m are determined. Then with a tape measure from NKK towards PC1, the tangent is measured by X = 27.32 m and from the point M perpendicular to lay the ordinate Y = 3.80 m.

The base of the perpendicular M can be determined by putting the segment ( k - X) = 0.35 m from PC1 in the direction of the NKK.

At the end of the ordinate a stake is scored and the guards are transferred from the tangent to this place on the curve. In a similar way, the other pickets to the CCM are taken out on the curve.

Carrying out the picket on the curve when it is on the second tangent is made similarly, only the origin of the curve is taken as the origin of coordinates.

12.6. Questions for self-control

1. What is a circular curve and for what it is arranged on the track?

2. What are the main elements of the curve called and how are they determined?

3. What points of a curve are called principal and how do they find their station value?

4. How to find the position of the main points of the curve on the ground?

5. What is the detailed breakdown of the curve for?

6. How to perform a detailed breakdown of the curve by the method of rectangular coordinates from tangents?

7. How to perform a detailed breakdown of the curve method of angles and chords?

8. How do they carry out pickets on a curve?