
5.1. Круговые кривые
На всех линейных сооружениях, предназначенных для движения транспорта, в местах изменения направления трассы для сопряжения прямых участков с целью плавного и постепенного поворота движущего транспортного средства устраивают закругления или кривые. Закругления могут быть любыми. Простейшим является дуга окружности определенного радиуса, т.е. круговая кривая.
На железнодорожных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 400 и 300 м. Конкретное решение о применении радиусов железнодорожных кривых принимают в соответствии с конкретными условиями и строительно-техническими нормами СТН Ц-01-95.
Круговая кривая характеризуется четырьмя главными точками и шестью основными элементами (рис. 8).
Главными точками кривой, которые определяют положение кривой на местности, являются: вершина угла ВУ; начало круговой кривой НКК; середина круговой кривой СКК; конец круговой кривой ККК.
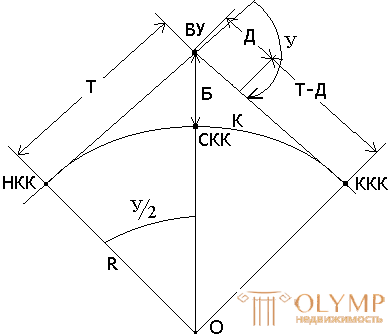
Рис. 8. Схема круговой кривой.
Основными элементами кривой являются:
1. Угол поворота трассы У.
2. Радиус закругления R.
Во время изысканий угол У вычисляют, а радиус R назначают. Остальные элементы находят по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НКК, О (рис. 8).
3. Тангенс кривой (касательная) Т – расстояние по прямой от вершины угла до начала или конца кривой.
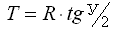
4. Длина кривой К от начала кривой до её конца.
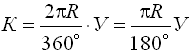
5. Биссектриса кривой Б – отрезок от вершины угла до середины кривой.
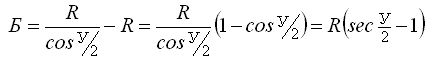
6. Домер Д – разность между длиной двух тангенсов и кривой.
Д = 2Т - К .
Все элементы кривой можно вычислить по вышеприведенным формулам. Но так как Т, K, Б и Д находятся в прямой зависимости от угла поворота и радиуса, то для их определения составлены специальные таблицы для разбивки кривых.
5.2. Вычисление пикетажа главных точек круговой кривой
Вычислить пикетажные значения главных точек кривой – значит узнать на каких пикетах и плюсовых точках они находятся.
Сначала определяют пикетаж вершины угла поворота ВУ, а затем находят пикетажное значение начала, конца и середины кривой
 .
.
Для контроля вторично вычисляют пикетажное значение конца кривой
КК = ВУ + Т - Д .
Пример (рис. 9): Определены: пикетаж ВУ ПК1+12.48 и основные элементы круговой кривой:

Найти пикетажные значения НКК, ККК, СКК. Расчет пикетажа главных точек кривой выполняется в следующей форме:
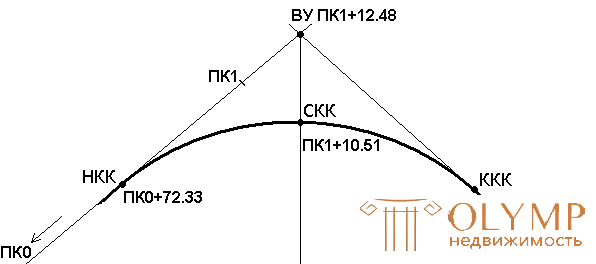
Рис. 9. Разбивка пикетажа с учетом кривой.

5.3. Разбивка кривой в главных точках на местности
Разбить кривую в главных точках на местности – значит найти положение её главных точек на оси линейного сооружения и закрепить их. Положение начала кривой НКК определяют, отложив вычисленное расстояние от ближайшего пикета.

Рис. 9. Разбивка пикетажа с учетом кривой.
В нашем примере (рис. 9) ближайшим пикетом является ПК1. От него к ПК0 откладывают расстояние 27,67 м. В этой точке забивают колышек, а на расстоянии 15 – 20 см по направлению трассы забивают сторожок и на нем записывают НКК ПК0 + 72.33.
Середину кривой СКК закрепляют, отложив от ВУ по направлению биссектрисы угла, образованного направлениями трассы, отрезок, равный Б.
На следующем, после вершины угла, направлении трассы откладывают величину домера (см. рис. 8), после чего продолжают разбивку пикетажа. При этом в месте отложения домера две точки – начало домера и его конец получают одно и тоже пикетажное наименование, благодаря чему в конце кривой пикетаж совпадает с пикетажем прямой. Положение ККК получают, отложив от конца домера расстояние , в примере оно равно 36.21 м. Найденное положение ККК закрепляют колышком и сторожком.
5.4. Детальная разбивка круговой кривой
По трем главным точкам точно построить кривую на местности невозможно, поэтому при строительстве трассы её обозначают рядом дополнительных точек. Данные работы называются детальной разбивкой кривой.
Расстояние между соседними точками на кривой К при детальной разбивке зависит от её радиуса R и характера сооружения, однако чем меньше R кривой, тем меньше значение К. при R > 500 м разбивку производят через промежутки k = 20 м, при 500 > R > 100 м k = 10 м, при R < 100 м k = 5 м.
Из всех существующих способов детальной разбивки, различающихся между собой по виду измерений и условиям использования, рассмотрим два способа.
Способ прямоугольных координат от тангенсов.

Рис. 10 . Способ прямоугольных координат от тангенсов.
Пусть М – начало кривой радиуса R (рис.10). Примем тангенс МА за ось абсцисс, а радиус МО за ось ординат. Положение точки N, кривой в принятой системе координат определяется абсциссой X1 и ординатой Y1.
Из прямоугольника ON1 находим

Угол j находим в зависимости от длины дуги k, через которую производят разбивку кривой:
 .
.
Тогда для точек 2, 3 и т.д. координаты вычисляют, подставляя в вышеприведенные формулы углы 2j, 3j и т.д.

По указанным формулам составлены таблицы, из которых по аргументам R и k можно выбрать значение Х и У.
В виду того, что значения k и Х близки между собой, в таблицах часто вместо графы Х дают значения (k – Х), называемые «кривая без абсциссы». Разбивку кривой производят с двух сторон – от начала и конца к середине кривой. По тангенсам отмеряют значение k и от полученной точки в обратном направлении откладывают значение (k – Х). Из данной точки восстанавливают перпендикуляр и откладывают на нём ординату Y.
Достоинство способа прямоугольных координат состоит в том, что каждая точка кривой выносится независимо от других с примерно одинаковой точностью.
Детальную разбивку кривой способом прямоугольных координат удобно проводить в открытой и непересеченной местности.
Детальная разбивка кривой при помощи углов и хорд.
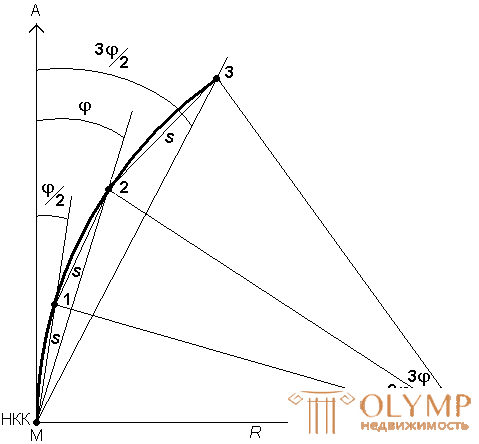
Рис. 11. Способ углов и хорд.
Данный способ основывается на том, что углы с вершиной в какой-либо точке круговой кривой, образованные касательной и секущей и заключающие равные дуги, равны половине соответствующего центрального угла (рис. 11).
Для разбивки кривой при помощи углов и хорд вычисляют центральный угол j, опирающийся на хорду s
 .
.
Рассчитывают углы ji между касательной и направлением на определяемые точки

Сначала выполняют разбивку кривой от её начала НКК до середины СКК. Для этого теодолит устанавливают в начале кривой НКК, совмещают нуль алидады с нулем лимба и вращением лимба направляют визирную ось по тангенсу. Затем, освободив алидаду, в сторону кривой откладывают от тангенса угол j1 = j/2 и по направлению луча визирования отмеряют лентой заданное расстояние s. Так находят точку 1. После этого откладывают угол j2 = j, а ленту переносят и совмещают её нуль с точкой 1. Взявшись пальцем у деления, равного s, вращают ленту вокруг точки 1 в сторону кривой до тех пор, пока деление не попадет на луч визирования. В данном месте отмечают точку 2. Продолжают действовать в той же последовательности, откладывая точку 3 и т.д.
Аналогичным образом выполняют разбивку кривой от её конца ККК до середины СКК.
В рассмотренном способе линейные измерения выполняют вблизи кривой, что выгодно при разбивке точек в стесненных условиях, например, на насыпи. Но так как положение последующей точки получают относительно предыдущей, то с возрастанием длины кривой точность её детальной разбивки быстро падает. В этом главный недостаток способа углов и хорд.
5.5. Вынос пикетов на кривую
Так как при разбивке пикетажа на трассе мерщики перемещаются по тангенсам кривых, то возникает необходимость выноса пикетов, расположенных на тангенсах, на кривые. Вынос пикетов на кривые выполняется способом прямоугольных координат и в принципе не отличается от детальной разбивки кривой с помощью данного способа. Разница лишь в том, что при детальной разбивке кривой необходимые данные берут из таблиц, в которых они даются через определенные расстояния по кривой (20, 10, 5 или 1м). При выносе пикетов с касательной (тангенса) на кривую такие данные находят также из таблиц, но при этом используют метод интерполирования.
Например, ПК1 лежит на тангенсе (рис. 12). Для того, чтобы его вынести на кривую, вычисляют расстояние k от ПК1 до НКК. Оно равно 27,67 м.
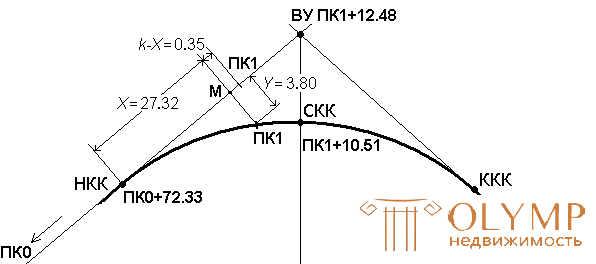
Рис. 12. Вынос пикетажной точки с тангенса на кривую.
Из таблиц при R = 100 м для k = 27,67 м путем интерполяции определяют X = 27,32 м и Y = 3,80 м. Затем рулеткой от НКК в сторону ПК1 по тангенсу отмеряют X = 27,32 м и из точки М по перпендикуляру откладывают ординату Y = 3,80 м.
Основание перпендикуляра М можно определить, отложив от ПК1 в направлении НКК отрезок (k – X) = 0.35 м.
В конце ординаты забивают кол и с тангенса в данное место на кривой переносят сторожок. Подобным образом выносят на кривую и другие пикеты до СКК.
Вынос пикета на кривую, когда она находится на втором тангенсе, производят аналогично, только за начало координат в данном случае принимают конец кривой.
12.6. Вопросы для самоконтроля
1. Что такое круговая кривая и для чего она устраивается на трассе?
2. Как называются основные элементы кривой и как они определяются?
3. Какие точки кривой называются главными и как находят их пикетажное значение?
4. Как находят положение главных точек кривой на местности?
5. Для чего выполняется детальная разбивка кривой?
6. Как выполняют детальную разбивку кривой способом прямоугольных координат от тангенсов?
7. Как выполняют детальную разбивку кривой способом углов и хорд?
8. Как производят вынос пикетов на кривую?
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Что бы оставить комментарий войдите
Комментарии (0)