1.4. The concept of the shape and size of the Earth

In geodesy to refer to the shape of the earth's surface, use the term "figure of the Earth . "

Knowledge of the shape and size of the Earth is necessary in many areas and above all to determine the position of objects on the earth's surface and correct its image in the form of maps, plans and digital terrain models.

The physical surface of the Earth consists of underwater (70.8%) and surface (29.2%) parts. The underwater surface includes a system of mid-ocean ridges, underwater volcanoes, oceanic troughs, underwater canyons, oceanic plateaus and abyssal plains. The surface part of the earth's surface is also characterized by a variety of forms. Over time, the surface of the Earth is constantly changing due to tectonic processes and erosion.

Fig. 2. Figure of the Earth (view from space)

The idea of ​​the figure of the Earth (Fig. 2) as a whole can be obtained by imagining that the entire planet is limited to the mentally extended surface of the oceans in a calm state.

The tier surfaces that envelope the Earth can be imagined. The one of them, which coincides with the average water level of the oceans in a calm state, i.e. at the moment of complete equilibrium of the entire mass of water in it under the influence of gravity, is called the main level surface of the Earth .

In geodesy, as in any other science, one of the fundamental principles is the principle of transition from the general to the particular. Based on it, to solve scientific and engineering problems on the study of the physical surface of the Earth, as well as other geodetic tasks, it is first necessary to determine the mathematical model of the Earth's surface.

What is the mathematical surface of the earth? What is the figure of the earth? What is its size?

Answers to these questions will be considered below.

1.4.1. Mathematical surface of the earth

Consider any material point A on the physical surface of the Earth (Fig. 3).

This point is influenced by two forces: the force of attraction F p, directed toward the center of the Earth, and the centrifugal force of rotation of the Earth around its axis F c, directed from the axis of rotation along the perpendicular. The resultant of these forces is called gravity F t.

At any point on the earth's surface, the direction of gravity, also called a vertical or plumb line, can be easily and simply determined using a level or plumb. It plays a very large role in geodesy. One of the axes of the spatial coordinate system is oriented in the direction of gravity.

If we construct a closed surface through point A, which at each of its points will be perpendicular to the plumb line (direction of gravity), then this surface can be taken as a mathematical one when solving some particular problems in geodesy. Such a surface is called level or horizontal. Its disadvantage is that it contains an element of uncertainty, i.e. through any point you can spend your level surface, and such surfaces will be countless.

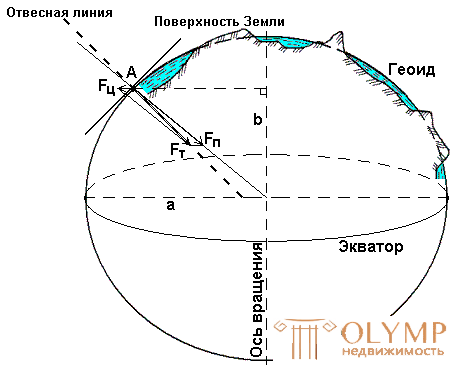
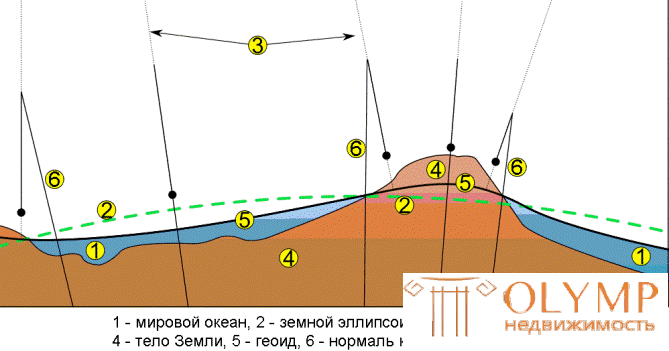
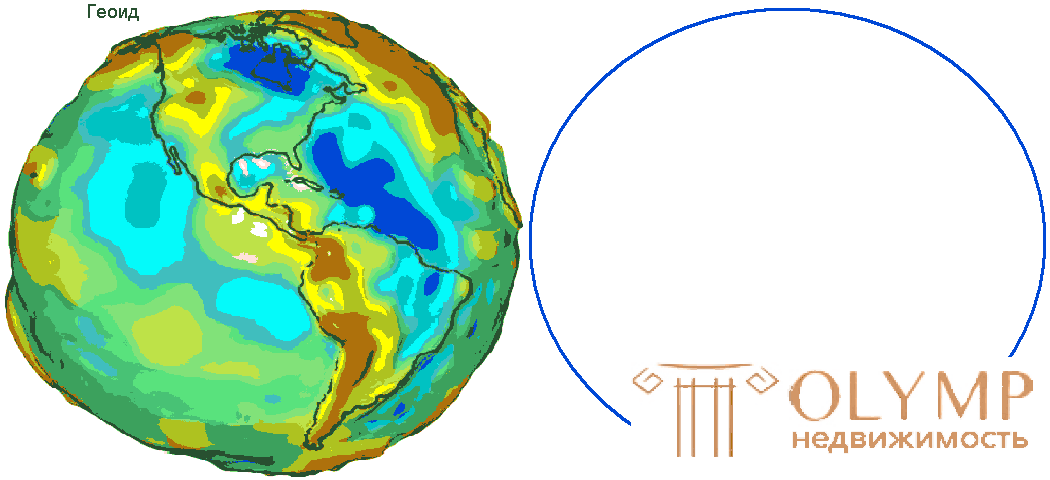
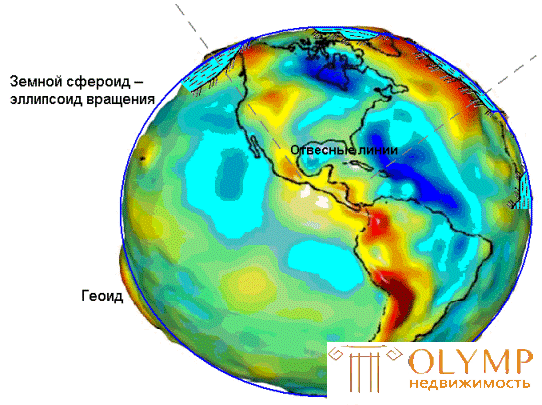
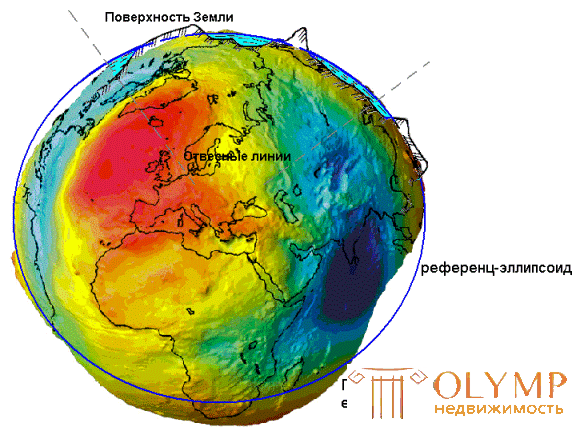
Fig. 3. Modeling the figure of the Earth

To eliminate this uncertainty in solving general geodesic tasks, the so-called general mathematical surface is taken, i.e. level surface, which in each of its points coincides with the average level of the seas and oceans at the time of complete equilibrium of the entire mass of water under the influence of gravity. Such a surface is called the common figure of the Earth or the surface of a geoid .

A geoid is a convex closed surface that coincides with the surface of water in the seas and oceans in a calm state and is perpendicular to the direction of gravity at any point (see Fig. 3).

The geoid shape depends on the distribution of masses and densities in the body of the Earth. Due to the uneven distribution of masses inside the Earth, the geoid does not have a regular geometric shape, and in the mathematical sense its surface is characterized by too much complexity. Therefore, where it is permissible, the geoid surface is replaced by approximate mathematical models, in which the earth spheroid is taken in some cases, the earth globe in others, and the horizontal plane , in topographic study of insignificant areas, a plane perpendicular to the vertical line at a given point.

The Earth spheroid - an ellipsoid of rotation is obtained by rotating an ellipse around its small axis b (see Fig. 3), which coincides with the axis of rotation of the Earth, with the center of the ellipsoid aligned with the center of the Earth.

The dimensions of the ellipsoid are selected under the condition of the best coincidence of the surface of the ellipsoid and the geoid as a whole (general earth ellipsoid) or its individual parts (reference ellipsoid).

The reference ellipsoid shape is best suited for the territory of a single country or several countries. As a rule, reference ellipsoids are accepted by law for processing geodetic measurements.

The most successful mathematical model of the Earth in the form of a reference ellipsoid was proposed by prof. FN Krasovsky with the big semi-axis a = 6378245 m, low - b = 6356863 m and the compression ratio at the poles a = (ab) / a = 1 / 298.3 ~ 1/300. The deviations of the Krasovsky ellipsoid from the geoid in the CIS territory do not exceed 150 m.

By the Decree of the Council of Ministers of the USSR No. 760 of April 7, 1946, the Krasovsky ellipsoid was adopted for the territory of our country as the mathematical surface of the Earth.

In engineering geodesy for practical calculations for the mathematical surface of the Earth take the ball with an average radius of R = 6371.11 km . The volume of the ball is equal to the volume of the earth's ellipsoid.

1.4.2. Physical surface of the earth

In a topographical study of the physical surface of the Earth, the surface and underwater parts are considered separately. The surface part (land) - terrain (territory) is the subject of topography study. The underwater part - the water area (the surface covered by the waters of the seas and oceans) is studied by oceanography .

In turn, the terrain is divided into a situation and relief .

The situation is called the set of permanent objects of the area: rivers, lakes, vegetation, road network, populated places, structures, etc. The boundaries between the individual objects of the situation are called terrain contours .

Relief (from Lat. Relevance - raise) is a collection of irregularities of the land, the bottom of the oceans and seas, varied in shape, size, origin, age and history of development.

Relief as a set of irregularities of the physical surface of the Earth is considered in relation to its level surface.

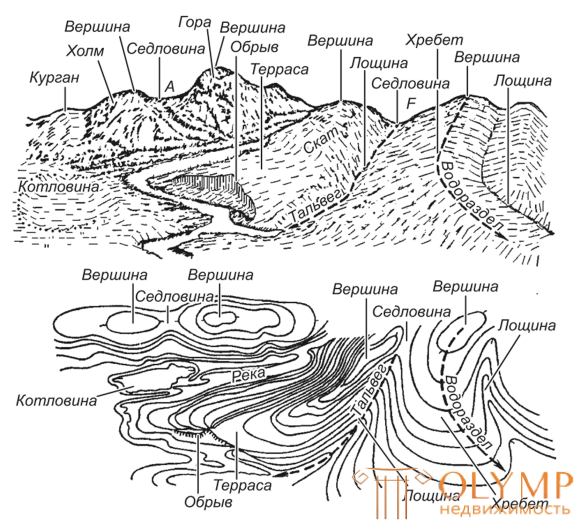
Fig. 4. Terrain

The relief is composed of positive (convex) and negative (concave) forms (Fig. 4) and is formed mainly as a result of a prolonged simultaneous impact on the earth's surface of endogenous (internal) and exogenous (external) processes.

Relief studies geomorphology .

The main forms of relief are the mountain, basin, ridge, hollow.