В геодезии для обозначения формы земной поверхности используют термин «фигура Земли».
Знание фигуры и размеров Земли необходимо во многих областях и прежде всего для определения положения объектов на земной поверхности и правильного её изображения в виде карт, планов и цифровых моделей местности.
Ещё в VI в. до нашей эры Пифагор считал, что Земля имеет шарообразную форму . То же открытие наиболее авторитетный автор в этом вопросе, Феофраст, отдаёт Пармениду.
Через 200 лет Аристотель доказал это, ссылаясь на то, что во время лунных затмений тень Земли всегда круглая.
Спустя ещё 100 лет Эратосфен по разнице в отклонении солнечных лучей от вертикали в полдень летнего солцестояния определил, что окружность земного шара приблизительно в 50 раз больше расстояния от Сиены до Александрии. Однако неизвестно, насколько точно в то время было измерено расстояние между этими городами .
То, что форма Земли должна отличаться от шара, впервые показал Ньютон. Он предположил, что она имеет форму эллипсоида и предложил следующий мысленный эксперимент. Нужно прокопать две шахты: от полюса до центра Земли и от экватора до центра Земли. Эти шахты заливаются водой. Если Земля имеет форму шара, то глубина шахт одинакова. Но на воду в экваториальной шахте действует центробежная сила, в то время как на воду в полярной шахте — нет. Поэтому для равновесия воды в обеих шахтах необходимо, чтобы экваториальная шахта была длиннее.
Дальнейшее развитие теории фигуры Земли отражено в работах Гюйгенса, Кассини, Клеро, МакЛорена, д'Аламбера, Лагранжа, Лапласа, Лежандра, Якоби, Дирихле, Пуанкаре и др.
Физическая поверхность Земли состоит из подводной (70,8 %) и надводной (29,2 %) частей. Подводная поверхность включает в себя систему срединно-океанических хребтов, подводные вулканы, океанические желоба, подводные каньоны, океанические плато и абиссальные равнины. Надводная часть земной поверхности также характеризуется многообразием форм. С течением времени поверхность Земли из-за тектонических процессов и эрозии постоянно изменяется.
В нулевом приближении можно считать, что Земля имеет форму шара со средним радиусом 6371,3 км. Такое представление нашей планеты хорошо подходит для задач, точность вычислений в которых не превышает 0,5 %. В действительности Земля не является идеальным шаром. Из-за суточного вращения она сплюснута с полюсов; высоты материков различны; форму поверхности искажают и приливные деформации.
В геодезии и космонавтике для описания фигуры Земли обычно выбирают эллипсоид вращения или геоид. С геоидом связана система астрономических координат, с эллипсоидом вращения — система геодезических координат.
По определению, геоид — это поверхность, всюду нормальная силе тяжести.
Если бы Земля была целиком покрыта океаном и не подвергалась приливному воздействию других небесных тел и прочим подобным возмущениям, она имела бы форму геоида. В действительности в различных местах поверхность Земли может значительно отличаться от геоида. Для лучшей аппроксимации поверхности вводят понятие референц-эллипсоида, который хорошо совпадает с геоидом только на каком-то участке поверхности. Геометрические параметры референц-эллипсоидов отличаются от параметров среднего земного эллипсоида, который описывает земную поверхность в целом.
На практике используется несколько различных средних земных эллипсоидов и связанных с ними систем земных координат.

Рис. 2. Фигура Земли (вид из космоса)
Представление о фигуре Земли (рис. 2) в целом можно получить, вообразив, что вся планета ограничена мысленно продолженной поверхностью океанов в спокойном состоянии.
Уровенных поверхностей, огибающих Землю, можно вообразить множество. Та из них, что совпадает со средним уровнем воды океанов в спокойном состоянии, т.е. в момент полного равновесия всей массы находящейся в ней воды под влиянием силы тяжести, называется основной уровенной поверхностью Земли.
В геодезии, как и в любой другой науке, одним из основополагающих принципов является принцип перехода от общего к частному. Исходя из него, для решения научных и инженерных задач по изучению физической поверхности Земли, а также других геодезических задач, сначала необходимо определиться с математической моделью поверхности Земли.
Что принимается за математическую поверхность Земли? Что является фигурой Земли? Какие у неё размеры?
Ответы на эти вопросы рассмотрим далее.
Рассмотрим любую материальную точку А на физической поверхности Земли (рис. 3).
На эту точку оказывают влияние две силы: сила притяжения Fп, направленная к центру Земли, и центробежная сила вращения Земли вокруг своей оси Fц, направленная от оси вращения по перпендикуляру. Равнодействующая этих сил называется силой тяжести Fт.
В любой точке земной поверхности направление силы тяжести, называемое ещё вертикальной или отвесной линией, можно легко и просто определить с помощью уровня или отвеса. Оно играет очень большую роль в геодезии. По направлению силы тяжести ориентируется одна из осей пространственной системы координат.
Если через точку А построить замкнутую поверхность, которая в каждой своей точке будет перпендикулярна отвесной линии (направлению силы тяжести), то данную поверхность можно принять в качестве математической при решении некоторых частных задач в геодезии. Такая поверхность получила название уровенной или горизонтальной. Её недостаток в том, что она содержит элемент неопределенности, т.е. через любую точку можно провести свою уровенную поверхность, и таких поверхностей будет бесчисленное множество.
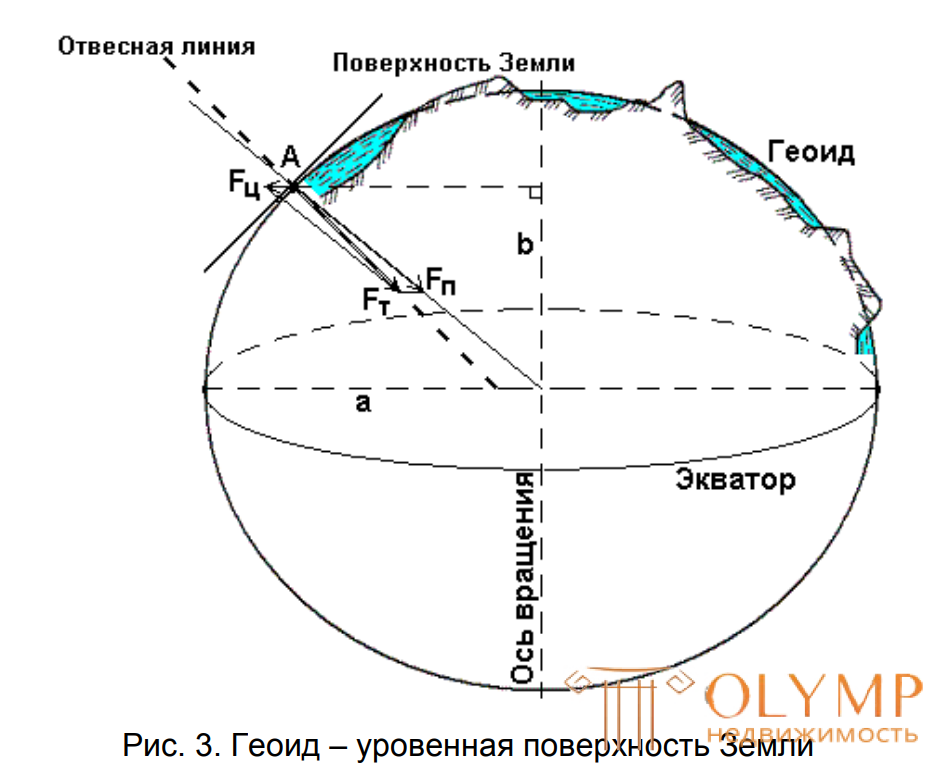
Рис. 3. Моделирование фигуры Земли
Для устранения этой неопределенности при решении общих геодезических задач принимается так называемая общая математическая поверхность, т.е. уровенная поверхность, которая в каждой своей точке совпадает со средним уровнем морей и океанов в момент полного равновесия всей массы воды под влиянием силы тяжести. Такая поверхность носит название общей фигуры Земли или поверхности геоида.
Геоид – выпуклая замкнутая поверхность, совпадающая с поверхностью воды в морях и океанах в спокойном состоянии и перпендикулярная к направлению силы тяжести в любой её точке (см. рис. 3).
Фигура геоида зависит от распределения масс и плотностей в теле Земли. Из-за неравномерного распределения масс внутри Земли геоид не имеет правильной геометрической формы, и в математическом отношении его поверхность характеризуется слишком большой сложностью. Поэтому там, где это допустимо, поверхность геоида заменяется приближенными математическими моделями, в качестве которых принимается в одних случаях земной сфероид, в других –земной шар, а при топографическом изучении незначительных по размеру территорий – горизонтальная плоскость, т.е. плоскость, перпендикулярная к вертикальной линии в данной точке.
Земной сфероид – эллипсоид вращения получается вращением эллипса вокруг его малой оси b (см. рис. 3), совпадающей с осью вращения Земли, причем центр эллипсоида совмещается с центром Земли.
Размеры эллипсоида подбирают при условии наилучшего совпадения поверхности эллипсоида и геоида в целом (общеземной эллипсоид) или отдельных его частей (референц-эллипсоид).
Фигура референц-эллипсоида наилучшим образом подходит для территории отдельной страны или нескольких стран. Как правило, референц-эллипсоиды принимают для обработки геодезических измерений законодательно.
Наиболее удачная математическая модель Земли в виде референц-эллипсоида была предложена проф. Ф. Н. Красовским с большой полуосью a=6378245 м, малой – b=6356863 м и коэффициентом сжатия у полюсов a = (a-b)/a = 1/298.3 ~ 1/300. Отклонения эллипсоида Красовского от геоида на территории СНГ не превышают 150 м.
Постановлением Совета Министров СССР № 760 от 7 апреля 1946 года эллипсоид Красовского принят для территории нашей страны в качестве математической поверхности Земли.
В инженерной геодезии для практических расчетов за математическую поверхность Земли принимают шар со средним радиусом R=6371.11 км. Объем шара равен объему земного эллипсоида.
При топографическом изучении физической поверхности Земли надводная и подводная части рассматриваются отдельно. Надводная часть (суша) – местность (территория) является предметом изучения топографии. Подводную часть – акваторию (поверхность, покрытую водами морей и океанов) изучаетокеанография.
В свою очередь местность разделяют на ситуацию и рельеф.
Ситуацией называют совокупность постоянных предметов местности: рек, озер, растительного покрова, дорожной сети, населенных мест, сооружений и т.п. Границы между отдельными объектами ситуации называются контурами местности.
Рельефом (от лат. relevo – поднимаю) называют совокупность неровностей суши, дна океанов и морей, разнообразных по очертаниям, размерам, происхождению, возрасту и истории развития.
Рельеф как совокупность неровностей физической поверхности Земли рассматривается по отношению к её уровенной поверхности.

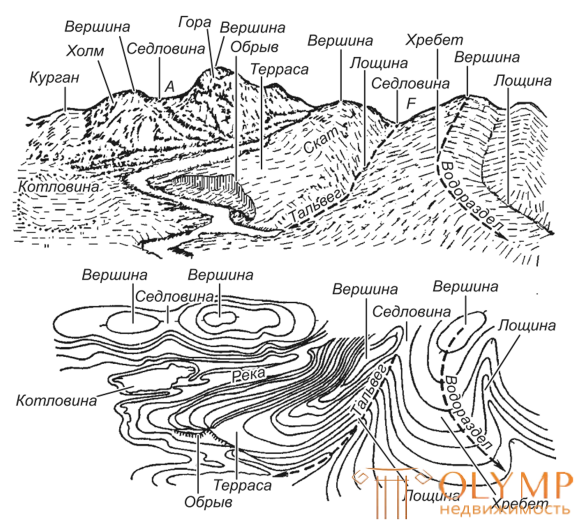
Рис. 4. Рельеф местности
Рельеф слагается из положительных (выпуклых) и отрицательных (вогнутых) форм (рис. 4) и образуется главным образом в результате длительного одновременного воздействия на земную поверхность эндогенных (внутренних) и экзогенных (внешних) процессов.
Рельеф изучает геоморфология.
Основными формами рельефа являются гора, котловина, хребет, лощина.

Рис. 2.8. Формы рельефа и их изображение горизонталями
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Что бы оставить комментарий войдите
Комментарии (0)