Centrally compressed elements . The cross section of elements of masonry structures at central compression is calculated by the formula
N ≤ mg φRA , (7)
where N is the calculated longitudinal force; The mg coefficient takes into account the effect of continuous load and is determined by the formula 2.10 with e 0g = 0; R-calculated resistance to masonry compression; A is the sectional area of the element; φ-coefficient of buckling, determined by the table. 2.5 depending on the value of the flexibility of the element λ and the elastic characteristics of the masonry a.
λ e = l0 / i ; λhpr = l0 √100 / r, (8)
r
where l0 is the calculated height (length) of the element; i is the smallest radius of inertia of the section; i = √ I / A.
FOR RECTANGULAR SECTION
λh = l 0 / h; λhpr = l 0 / h * √100 / a, (9)
where h is the smaller size of the section of the element.
The coefficient mg is determined by the formula
mg = 1-η * Ng / N (1 + 1.2 * e 0g), (10)
h
where η-coefficient taken from the table. 2.6; Ng-calculated longitudinal force from long-term load; N-longitudinal force from all loads; h-height of the section; e og-eccentricity from long-acting loads.
The calculated height (length) l o is taken depending on the conditions of the walls on the horizontal and vertical supports (Table 8).
Objective: 1. Determine the strength of a brick center-loaded column, supported on the wall of a monolithic ceiling. A column of silicate brick brand 125, size 51 × 64 cm; height H = 6.5 m. A solution of cement grade 50 on lightweight substitutes with superplasticizer.
The decision . According to the table. 8 we find l o = 0.8, H = 0.8 * 6.5 = 5.2 m. We calculate the flexibility λh = l o / h = 520/51 = 10.2 According to the table. 3 we find a = 750 * 0.7 = 525.
The coefficient φ is found in the table. , taking into account λhпр
λhpr = l o / h = √1000 / a = 520/51 = 1000/525 = 14.1.
According to the table. 2.8 for λhpr = 14.1 by interpolation φ = 0.787. When h> 30 cm mg = 1 and the estimated resistance of the masonry on the table. 1 R = 1.7 × 0.85 = 1.4 MPa. The cross-sectional area A = 51 × 64 = 3264 cm2 = 0.33m2> 0.3m2 and mh = 1. The strength of the brick centrally loaded column is determined by the condition
N = mgφRA = 1 * 0.787 * 1.4 * 3264 = 35 962.7 kgf = 359.6 kN.
Task: 2. Check the bearing capacity of a centrally loaded brick pillar with height H = 4.2 m and a cross section of 51 × 51 cm made of ceramic brick of plastic pressing of mark 75 on cement-lime mortar of mark 25. The column is supported by a precast reinforced concrete floor. The load on the pole N = 320 kN (32 ts), taking into account the reliability coefficient for the value γn = 0.95.
Decision. According to the table. 2.7 l o = 0.9 * H = 0.9 * 4.2 = 3.8m; λh = l o / h = 380/51 = 7.45. According to the table. 7.5 a = 500. Find φ in the table. 2.5 φ = 0.865 and mg = 1 (h> 30 cm); on the table. 1 R = 0.9 MPa. The bearing capacity of the column is determined by the condition (7).
N Sech = 1 * 0.865 * 7.2 * 2600 = 16,192.8kgs = 162kN
Nsech = 162kN <N = 320
The strength of the brick pillar is not provided. It is necessary to increase the cross-sectional area, adopt higher grade materials or provide reinforcement.
Task: 3. determine the width of the brick pier 51 cm thick and 4.7 m high. The effective force is N = 800 kN taking into account the reliability coefficient for the intended purpose γn = 0.95; overlap hinge.
Decision. We accept silicate brick of mark 125 with R = 1.4 MPa, grout grade 25. The width of the pier is determined from equation (7) with mg = 1 and φ = 1.
b = N / Rh = 80,000 = 112cm
14 * 51
width is taken as a multiple of the brick size b = 129 cm. we define a = 750 (see table. 3); l o = H and λh = l o / h = 470/51 = 9.2; mg = 1 (with h> 30 cm) and according to the table. 7 φ = 0.865. The bearing capacity of the pier on (7)
N Sech = 1 * 0.865 * 14 * 129 * 51 = 79 671 * 7kgs = 796.6 kN <800 kN
Strength is not ensured, therefore, it is necessary to accept a brick of mark 150 (R = 1.5 MPa) with a solution of mark 25 and repeat the calculations.
Task: 4. Determine the bearing capacity of the wall section. The masonry of the internal bearing wall is made of the largest continuous concrete blocks of brand 50. The wall thickness is h = 30cm, width is b = 100cm, and the height of the floor is 420cm. Long load Ng = 500kN; total N = 1300 kN taking into account the reliability coefficient for the intended purpose γn = 0.95.
The decision . We define l o = 0.9 Net = 0.9 * 4.2 = 3.8 m;
λh = l o / h = 380/30 = 12.66.
Determine the ratio of the height of the wall to the thickness:
β = Nat / h = 420/30 = 14 <25.
According to the table. 5 with a = 1500 φ = 0.876. determine mg (with h≤30cm)
mg = 1-η * N g / N = 1-0,057 * 500 = 0.978
1300;
η = 0.057 taken on the table. 6. for large concrete blocks (Table 2) R = 5.7 MPa. The cross-sectional area A = 30 × 100 = 3000 cm2 = 0.3m2, i.e. mk = 1. Bearing capacity of 1m wall by the condition (7).
Nsech = mg φRА = 0.987 * 0.876 * 57 * 3000 = 146 500kgs = 1465 kN <1800 kN.
N sech = 1465 kN <N = 1800 kN.
The strength of the wall is not provided. You need to change the cross-section (width) or accept materials with higher strength properties and repeat the calculations.
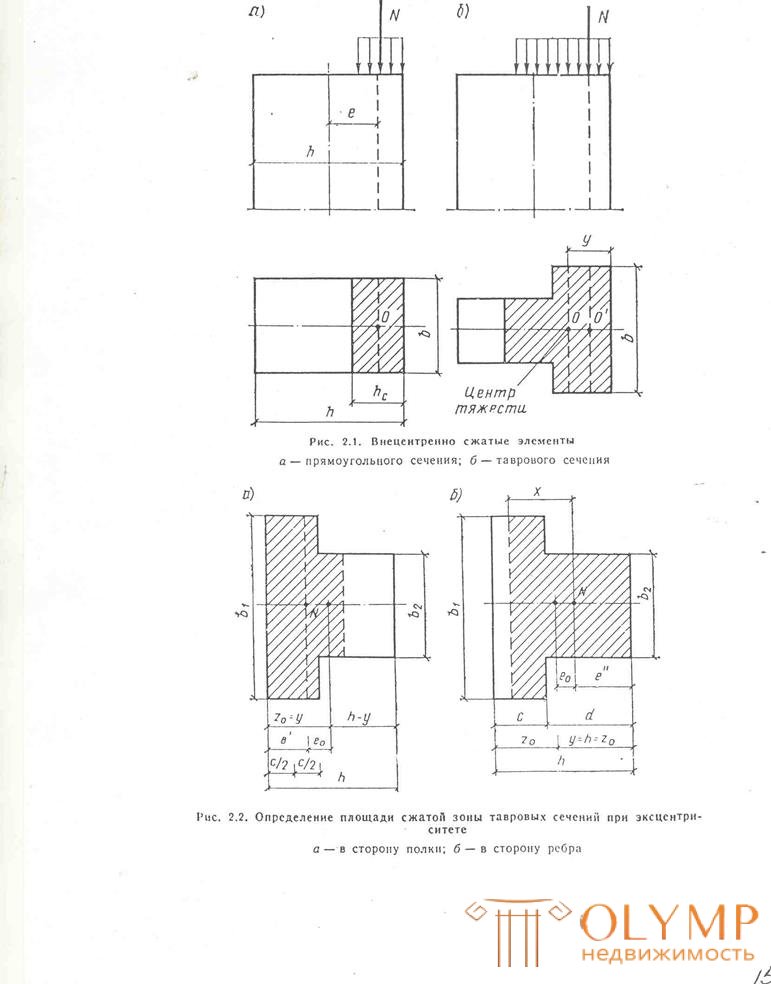
Centerlessly compressed elements . When calculating eccentrically compressed elements of unreinforced masonry, condition (7) is written in the form:
N≤mg φ1RAcω, (11)
and for a rectangular section
N≤mgφ1RA (1-2ℓ0 / h) ω (12)
where Ac = A (1-2ℓ0 / h); (13)
φ1 = (φ + φс) / 2;
φ1 = φ [1- l o / h * (0.06 * l o -0.2)]; (14)
he
where Ac is the area of the calculated compressed part of the section, which is determined under the assumption of a rectangular diagram of compression stresses (see Fig. 2.1); эксo-eccentricity of the longitudinal calculated force N relative to the center of gravity of the section; l o is the calculated height of the elemental moment; ω-coefficient taken from the table. 9: mg-coefficient taking into account the decrease in strength during long-term load, can be determined by the formula 10; when h≥30 cm ( i ≥ 8.7 cm), the coefficient is mg = 1.
The area of the compressed zone of rectangular cross-section (Fig. 2.1, a)
Ac = b (h-2ℓ0) (15)
For a T-section, the distance x from the point of application of force N to the boundary of the compressed zone is determined depending on the eccentricity.
With an eccentricity in the direction of the shelf (Fig. 2.2, a )
x = √b1c / b2 * (2ℓ ׀- c) + (ℓ ׀- s) 2, (16)
With an eccentricity in the direction of the edge (Fig. 2.2, b )
x = √ b2d / b1 * (2ℓ ׀׀- d) + (ℓ ׀- d) 2, (17)
if ℓ׀׀ <d / 2, then x =

For large eccentricities ( e > 0.45 y), the area Ac can be determined by the formula
Ac = 2b (y-ℓo) (18)
For T-sections, the position of the center of gravity and the moment of inertia can be determined from the graphs.
Task: 5. to determine the strength of the wall of a T-section of masonry, loaded with a force of N = 900kN, taking into account the reliability coefficient for the intended purpose γn = 0.95 (eccentricity towards the rib) and the moment M = 15tc * m = 150 kN * m. floor height 4,2m. The masonry is made of ceramic brick of plastic extrusion of the 150 grade on the 50 grade solution. The overlap of a single-span building works according to an elastic scheme.
The geometric dimensions of the cross section are given in Fig. 2.3.
The decision . The calculated resistance of masonry to compression is R = 1.8 MPa (Table 1.). Eccentricity ℓ0 = M / N = 150/9000 = 0.17 m = 17 cm. We calculate in accordance with condition (11). The cross-sectional area A = 51 * 116 + 52 * 51 = 8568 cm2 = 0.86 m2> 0.3 m2.
Elastic characteristic a = 1000 (tab. 3). we determine the distance of the center of gravity of the section from the edge of the shelf by a = ho / h = 51/103 = 0.495; β = ho / υ = 51/115 = 0.44 x = 0.402; η = 0.053; zo = x h = 0.402 * 103 = 41.4cm.
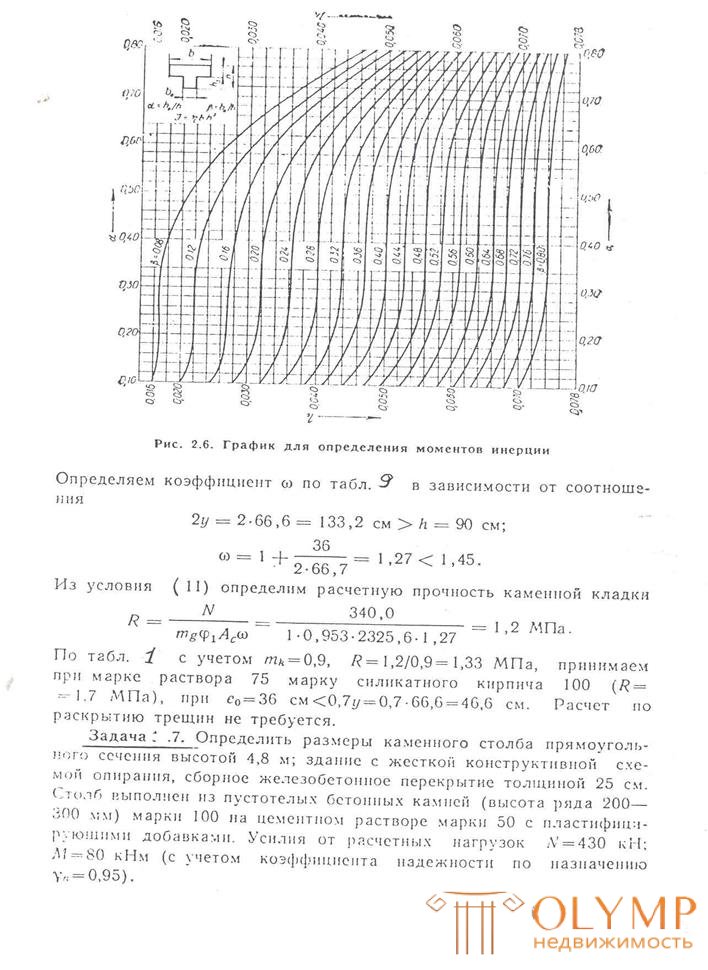
The moment of inertia (according to the graph of Fig. 2.6) І = nbh3 = 0.053 * 116 * 1033 = 6 718 085 cm4. The radius of inertia of the section r = √I / A = 28 cm. When r> 8.7 cm, mg = 1; l о = 1.5 (Н-Нn) (according to table 2.7) l о = 1.5 (4.2-0.2) = 6.0 m. The flexibility of the pier l 2 = ℓ0 / r = 6 / 0,28 = 21,4. According to table 5. with a = 1000; φ = 0.634. then by condition. (14)
φ1 = φ [1-ℓ0 / h (0.06 l 0 -0.2)] =
he
= 0.634 [1-17 / 103 (0.06 600 -0.2)] = 0.616;
98
Where h = 3,5r = 3,5 * 28 = 98cm.
Find the distance from the point of application of force N to the boundary of the compressed zone
y = h-z0 = 103-41.4 = 60.6 cm;
ℓ׀׀ = y-ℓ0 = 60.6-17 = 44.6 cm.
The condition ℓ׀׀ ≤ d / 2 = 52/2 = 26 cm is not satisfied, therefore, we calculate by the formula: (17)
x = √51 * 52/116 (2 * 44.6-52) + (44.6-52) 2 = 30.08 cm.
The height of the compressed zone section hc = ℓ ׀׀ + x = 44.6 + 30.08 = 74.68cm.
The area of the compressed section of the section Ac = 74.68 * 51 + (116-51) (74.68- 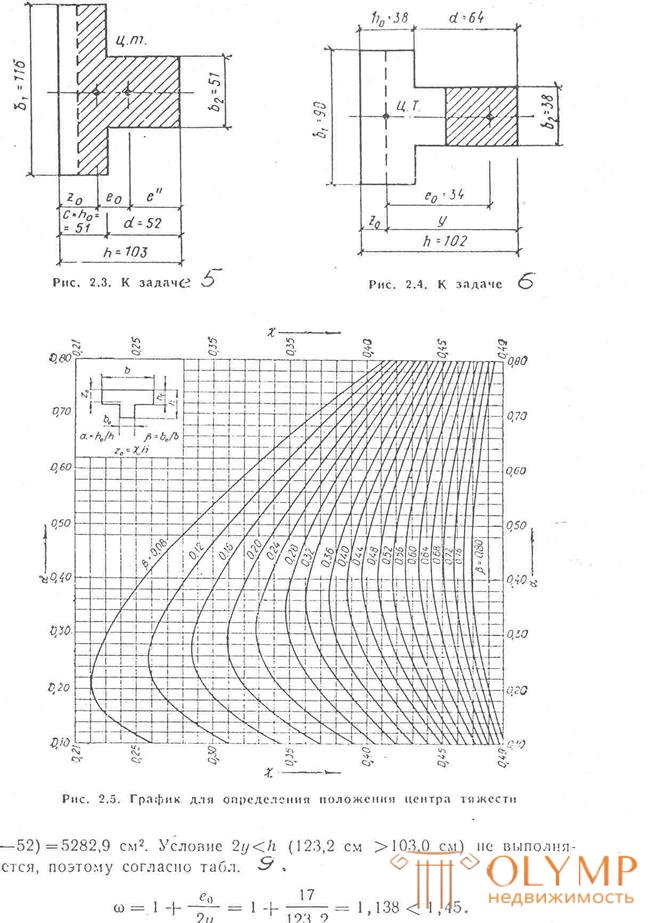
Bearing capacity of the pier is calculated from the condition (11)
N≤1 * 0.616 * 18 * 5282.9 * 1.138 = 666.6 kN <900 kN.
Strength of the pier is not provided. You need to increase the cross section or apply more durable masonry materials. Calculate repeat. Since ℓ0 = 17cm <0.7u = 43.1cm, the calculation for crack opening is not required.
Task: 6. Determine the strength of the Tauri stone masonry and the brand of brick, the geometrical dimensions of which are shown in Fig. 2.4. Masonry with a loaded force N = 34ts = 340 kN taking into account the reliability coefficient for the intended purpose γn = 0.95, acting with eccentricity ℓ0 = 36cm in the direction of the rib, the overlap is monolithic, the height of the pier is Nf = 5.8m. Brand of cement mortar 75, using plasticizers, masonry is made of silicate brick.
The decision . For masonry of silicate bricks on cement mortar brand 75 table. 3 a = 750. The area of the wall A = 38 * 64 = 2432 cm2 = 0.23 m2 <m2. According to graphs fig. 2.5 we find the coefficients:
A = h0h = 38/102 = 0.372; β = i0 / u = 38/90 = 0.421;
X = 0.393; η = 0.051.
Center of gravity distance from the edge of the shelf
z0 = xh = 0.393 * 90 = 35.37 cm.
The moment of inertia of the section (according to the graphs of Fig. 2.6)
J = ηbh2 = 0.051 * 90 (102) 3 = 4 870 944 cm4
y = h-z0 = 102-35,4 = 66.6 cm.
The radius of inertia is r = √ A = 28.8 cm. Accept mg = 1, since r> 8.7 cm.
The flexibility of the pier λ2 = l 0 / r = 0.8 * 580 / 28.8 = 16.1. According to the table. 2.5 coefficient of buckling φ = 0.98. From the condition (2.14)
φ1 = 0.98 [1-34 / 90 (0.06 0.8 * 580 -0.2)] = 0.953,
100.8
where he = 3,5 r = 3,5 * 28,8 = 100,8 cm.
The distance from the point of application of force N to the boundary of the compressed zone
ℓ׀ = y-ℓ0 = 66.6-36 = 30.6 cm <d / 2 = 64/2 = 32 cm.
Compressed masonry zone height under the condition x = ℓ ׀
hc = 2x = 2 * 30.6 = 61.2 cm.
The area of the compressed zone Ac = 61.2 * 38 = 2325.6 cm2
The decision . Determine the parameters of masonry: strength R = 1.7 MPa according to the table. four; elastic characteristic a = 1500 table. 3 Eccentricity of the longitudinal force relative to the center of gravity of the section
ℓ0 = M / N = 80/430 = 0.186m = 18.6cm.
The selection of the section is made by the method of successive approximations taking into account the coefficients mg; φ1; (1-2ℓ0 / h); ω by the formula
A = N / [mgφ1R (1-2ℓ0 / h) ω].
Let us set as an approximation the product of these coefficients, equal to 0.5. Then
A = N / 0.5R = 43 000 / 0.5 * 17 = 5058.8 cm2
With h = b = √5058.8 = 71.7 cm. Accepted 79cm. The estimated column length is l 0 = 0.9 (Ne-Nper) = 0.9 (4.8-0.25) = 4.1 m. Flexibility λр = l 0 / h = 410/79 = 5.18.
When a = 1500 and λh = 5.18 buckling coefficient φ = 0.988 (see Table 5).
By condition (14) with he = h = 79cm
φ1 = 0.988 [1-18.6 / 79 (0.06 518 -0.2)] = 0.943
79
According to the table. 9 ω = 1 + 18.6 = 1.23 <1.45.
79
Required area when h = 79cm
A = 43,000 / [1 * 0.943 * 17 * (1-18.6 / 79) * 1.23] = 2832.1 cm2.
Then the size of the second side of the pillar
b = A / h = 2832.1 / 79 = 35.8 cm.
The closest size, multiple to the size of the stone is b = 59 cm, i.e.
A = bh = 59 * 79 = 4661cm2.
Coefficient mg = 1 for h> 30 cm. Bearing capacity of a rectangular post column according to the condition (12)
N = 1 * 0.943 * 17 * 4661 (1-2 * 18.6 / 79) 1.23 = 486.8 kN> 430 kN.
The accepted section of the post is sufficient. Relative eccentricity
ℓ0 / h = 18.6 / 39.5 = 0.47 <0.7cm
(with y = h / 2), therefore, the calculation for the crack opening is not performed.
Что бы оставить комментарий войдите
Комментарии (0)