Compressed elements with random eccentricities.

The eccentrically compressed elements experience a longitudinal compressive force N applied with an eccentricity relative to the center of gravity of the section, or the force N and a bending moment M. The simultaneous action of force N and moment M is equivalent to the action of only one force N applied with eccentricity l0 = M / N relative center of gravity of the section. There is a class of structures in which, in accordance with the static calculation, the longitudinal force acts on an axis passing through the center of gravity of the section.

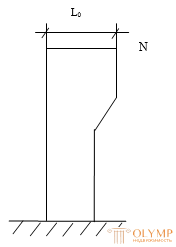
However, in fact, in these structures there is an eccentricity caused by random causes (heterogeneity of the properties of materials over the section, the initial curvature of the element, etc.)

Therefore, when calculating the strength of such elements, random eccentricity should be taken into account; lo, taken to be the larger of:

lo = 1/600; lo = h / 30 where; l is the length of the element, h is the size of the cross section.

The eccentrically compressed elements with random eccentricities include the upper truss belts with nodal load transfer, compressed truss lattice elements.

Design features of compressed elements with flexible longitudinal reinforcement and clamps. The cross section of the compressed elements is assumed: at small eccentricities - square, round, circular, for large - rectangular, I-beam.

The cross-sectional dimensions are determined by calculation and, for unification, taken as multiples of 50mm, if the size of the cross section does not exceed 500mm, and multiples of 100mm - for large sizes. For columns, concrete B15 ... B30 is usually used. Depending on the features of reinforcement, compressed elements are distinguished:

1) by type of longitudinal reinforcement

a) with flexible longitudinal reinforcement and clamps

b) with rigid (bearing) longitudinal reinforcement,

2) by type of transverse reinforcement :

a) with conventional transverse reinforcement (clamps),

b) with indirect reinforcement in the form of spirals, rings or grids.

The reinforcement of compressed elements considered in the calculation consists of longitudinal and transverse rods (clamps) located at equal distances from each other. Longitudinal reinforcement is placed on the calculation and takes part of the load acting on the element. Clamps are designed to ensure the design position of the valve and to prevent buckling of the longitudinal rods under the action of an external load. In addition, clamps prevent the development of lateral deformation of the element, thereby increasing the resistance of concrete to compression.

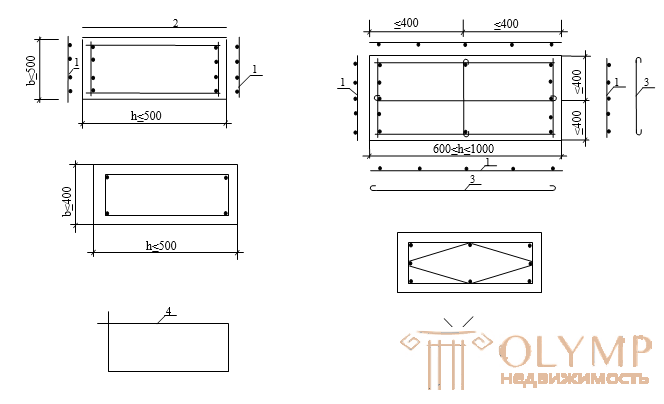
The saturation of the cross section of compressed elements with longitudinal reinforcement is estimated by the reinforcement ratio m or the reinforcement percentage m%. The optimal percentage of reinforcement for economic reasons, take 1 ... 2%. The minimum% is 0.05 ... 0.25%; maximum - 3%.

For longitudinal reinforcement, it is advisable to use hot-rolled steel grades AII and AIII with a diameter of 12 to 40 mm.

In elements with a random eccentricity, the longitudinal working reinforcement is placed around the perimeter of the rod so that the column can better perceive the bending moment from random side effects and the calculated lateral forces

The maximum allowable distance between the axes of the rods is 400mm. If the distance between the axes of the longitudinal rods is> 400 mm, then additional rods with a diameter of not <12 mm should be installed between them. Columns with a section of 400x400mm can be reinforced with 4 rods. If the flat frames of the opposite faces of the column have intermediate longitudinal rods, the latter through one and no less than 400 mm are connected with hairpins.

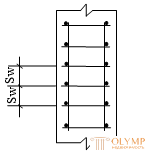
Transverse reinforcement in compressed elements set constructively.

The distance between the transverse rods is prescribed 20d - in welded frames, 15d - in knitted and not more than 500mm.

The diameters of the transverse rods dsw in the welded frameworks are prescribed according to the conditions of weldability, and in the knitted - not less than 5 mm and not less than 0.25 d. For transverse reinforcement, steel grades Al, Bpl, AIII are used.

Strength calculation of compressed elements with random

eccentricities.

For elements of rectangular cross-section with a calculated length of L <20h

(h is the larger size of the cross section).

It is allowed to calculate columns according to the formulas of central compression:

1) N <(f • (Rb • A + Rsc • Asc) (one)

Where <f is the coefficient of stability or buckling

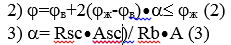
VF and FW see table 4.3 p.135 "Building structures" (Tsai), depending on the flexibility of the element l = l0 / h and the ratio N / N

l0 - the estimated length of the column, taken equal to:

a) in high-rise buildings - floor height h

b) in single-storey industrial buildings - l0 = 1.2 (H + 0.15),

where H is the mark of the bottom of the beam or truss.

In practice, there are 3 types of tasks:

Type 1 Task

Heaving capacity of a centrally compressed element with known data on cross-sectional dimensions, reinforcement, materials and load is checked using formula 1, for which j is determined first by formula 3 and table data.

Type 2 Task

Given:

b 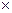h (see)

Ndl, Ncr (kN)

AT; 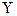vi;

Reinforcement class;

Find Asc (cm2)

The problem is solved by a method of successive approximation.

Accept j = 1

Find N = Ndl + Ncr (kN)

Find the approximate area of ​​Asc reinforcement

Asc = N / f • Rss-A • Rb / Rsc (cm2) (4)

Find the true value of the coefficient j, for which we first find:

l = l0 / h and the ratio N / N, then 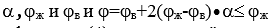on f-le (2)

Again, we calculate Asc no to formula (4), taking it as the final decision.

If the calculation results in a negative value, it means that compressed reinforcement is not required by calculation and we take it at min% reinforcement:

mmin = Asc / A = 0.0025 from where Asc = 0.0025 • A (cm2) but not less than 12mm.

Type 3 Task

The lateral dimensions of the centrally compressed element and the cross-sectional area of ​​the reinforcement for a given load, the calculated length and materials are determined, initially giving the values ​​j = 1, m = 1% = 0.01,

From condition (1), the following is calculated: 4) A = N / j • (Rb + m • Rsc) (4)

Next, find the dimensions of the cross section b = h = 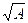and designate the sizes taking into account unification multiples of 50 mm.

Then, the flexibility of the element l = l0 / h and the ratio N / N are calculated and Asc is selected as in type 2 problem. If it turns out that the% of reinforcement of the calculated section does not satisfy the condition mmin≤m £ mm, then the transverse dimensions of the element should be changed and re-calculated j, Asc. The section can be considered matched satisfactorily if m = 1 ... 2%