Определение углов закручивания брусьев круглого поперечного сечения и расчеты на жесткость кратко

Угол взаимного закручивания концевых сечений участка стержня длинойопределяется по формуле:

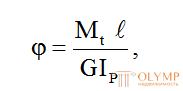(6.11)

здесь – крутящий момент, постоянный по длине участка;– длина участка;G– модуль упругости материала при сдвиге (модуль упругости 2-го рода).

Произведение 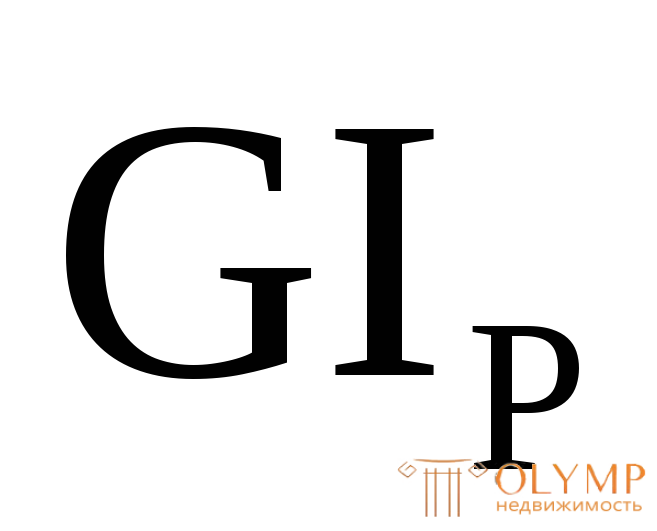называетсяжесткостью поперечного сечения при кручении.

Если крутящий момент по длине участка M_t(x) есть величина переменная, то взаимный угол закручивания концевых сечений участка определится по формуле:

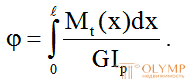. (6.12)

Чтобы определить полный угол закручивания  какого-либо сечения j бруса по отношению к закрепленному сечению (там угол закручивания равен нулю), нужно взять сумму углов закручивания на всех n участках, заключенных между неподвижным (закрепленным) и рассматриваемым j-м сечениями:

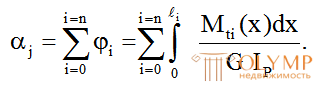(6.13)

Относительный угол закручивания 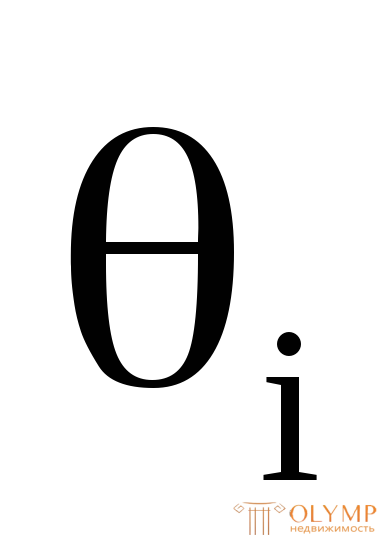, т.е. угол закручивания, приходящийся на единицу длины, определяется по следующей формуле:

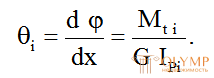(6.14)

Условие жесткости бруса, работающего на кручение, если ограничен относительный угол закручивания , запишется в виде

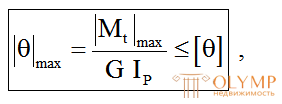(6.15)

где – допускаемый относительный угол закручивания (рад/м);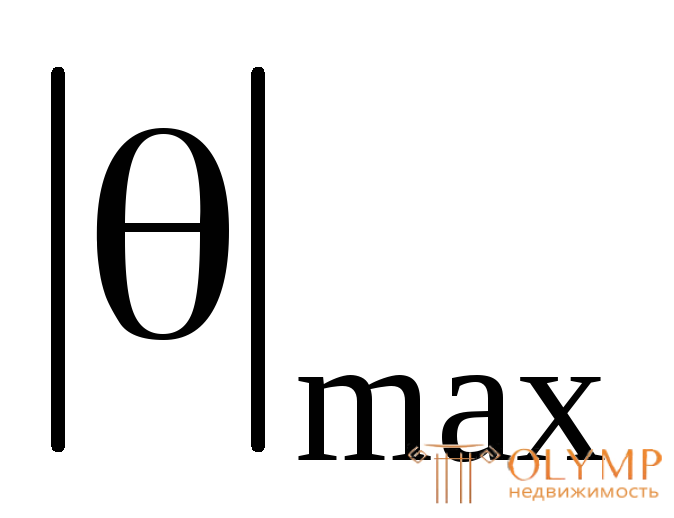– наибольший по модулю относительный угол закручивания по длине бруса.

Используя условие жесткости (6.15), можно решать следующие задачи:

1. Проверить жесткость бруса, т.е. проверить выполнение условия (6.15).

2. Определить диаметр бруса из условия жесткости (подбор сечения).

Для этого из формулы (6.15) вычисляем требуемое значение полярного момента инерции: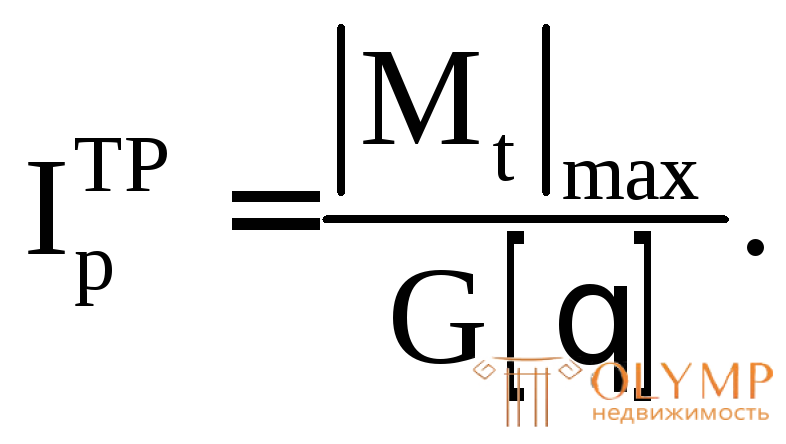

Приравнивая требуемую величину к выражению (6.6) или (6.8), т.е.I_=, определим диаметр поперечного сеченияdили d_ext.

3. Вычислить допускаемое значение крутящего момента для бруса заданного диаметра при известном значении G:

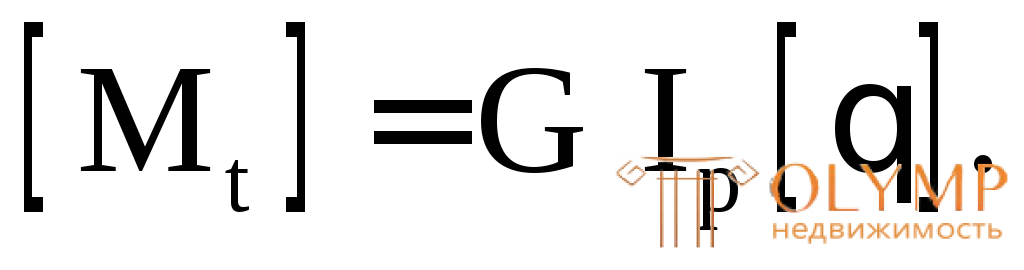
Если ограничен полный угол закручивания сечения (в радианах) для всего стержня, то условие жесткости запишется в следующем виде:

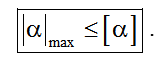. (6.15)'

Здесь 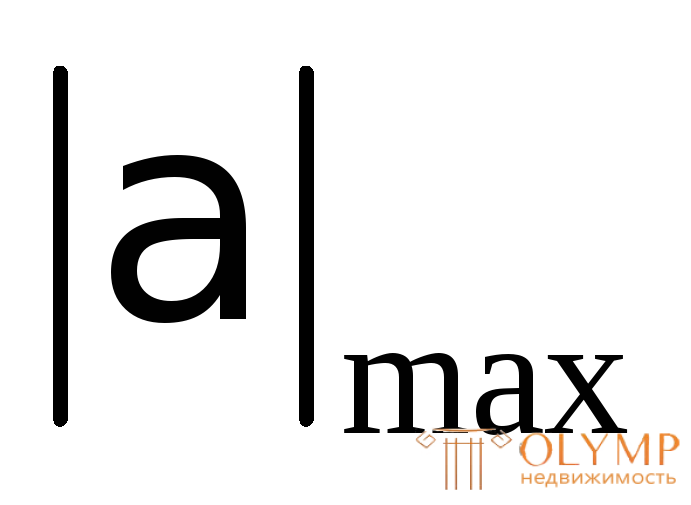– наибольший полный угол закручивания сечения по отношению к закрепленному, который берется из эпюры.

При подборе сечения по данному условию жесткости эпюра строится при неизвестном диаметре, при GI_p=const.

Используя условие жесткости (6.15)', также можно решать приведенные выше три типа задач.

ПРИМЕР 6.1

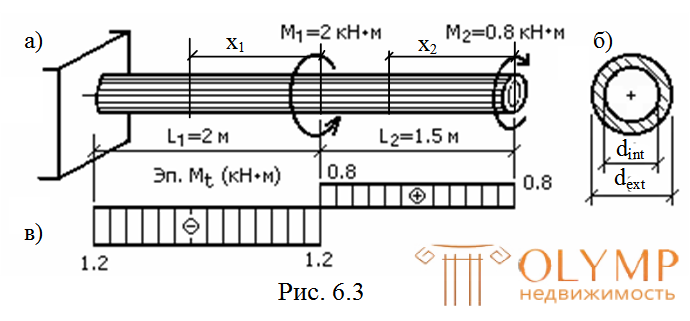
Требуется подобрать диаметр бруса кольцевого сечения, (рис. 6.3), по условиям прочности и жесткости при следующих исходных данных:

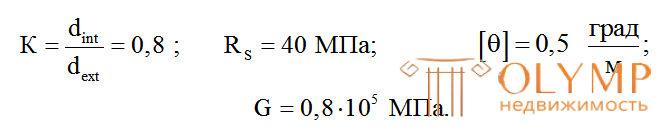
РЕШЕНИЕ

1. Построение эпюры крутящих моментов.Наметим два грузовых участка и в пределах каждого проводим произвольное сечение.

Рассматривая от каждого сечения правую отсеченную часть (так как там нет опоры), вычисляем величины крутящих моментов, используя следующее рабочее правило, вытекающее из метода сечений:

Крутящий момент в любом сечении бруса численно равен алгебраической сумме моментов всех внешних сил, действующих по одну сторону от сечения относительно продольной оси бруса в месте сечения.

Правило знаков для крутящих моментов:

К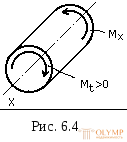рутящий момент будем считать положительным, если при взгляде на сечение со стороны внешней нормали он будет закручивать отсеченную часть по ходу часовой стрелки. В этом случае внешний закручивающий момент М_Х будет действовать против хода часовой стрелки(рис. 6.4). Знак Мбудет отрицательным, если направление момента М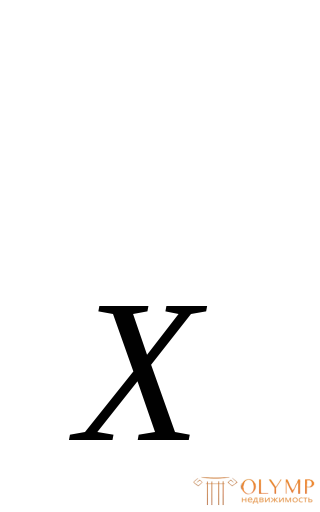будет противоположным.

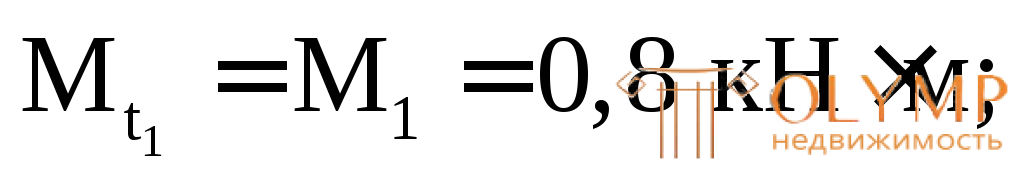
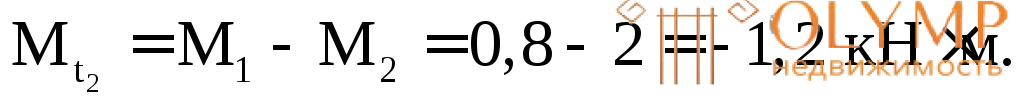
На обоих участках крутящие моменты постоянны. По этим значениям строим эпюру (см. рис. 6.3в), из которой получаем: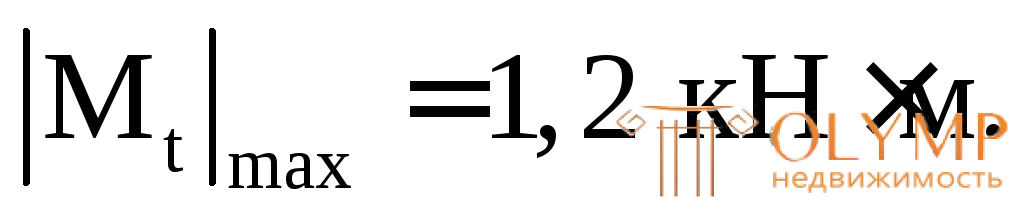

2. Подбор сечения из условия прочности.

Определяем требуемый полярный момент сопротивления из условия прочности:

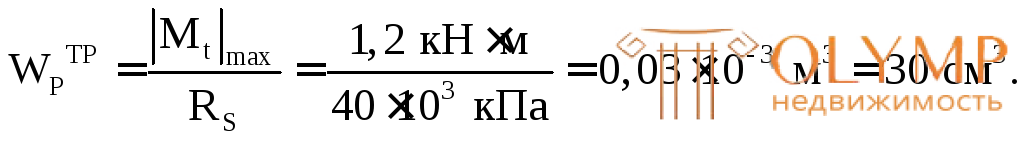
Используем соотношение (6.8) для бруса кольцевого сечения: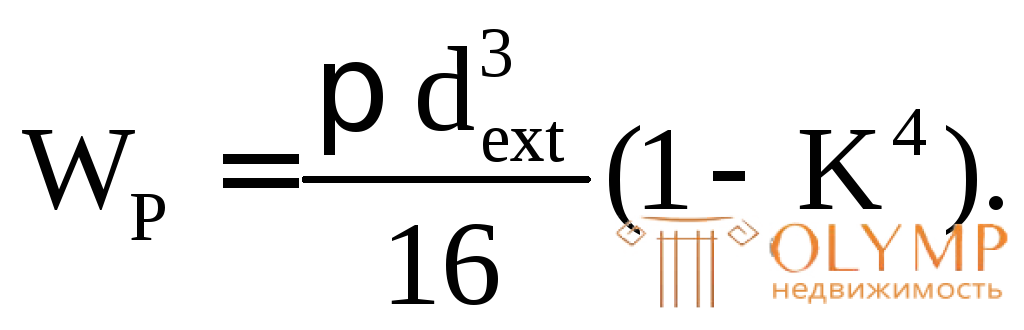

Приравниваем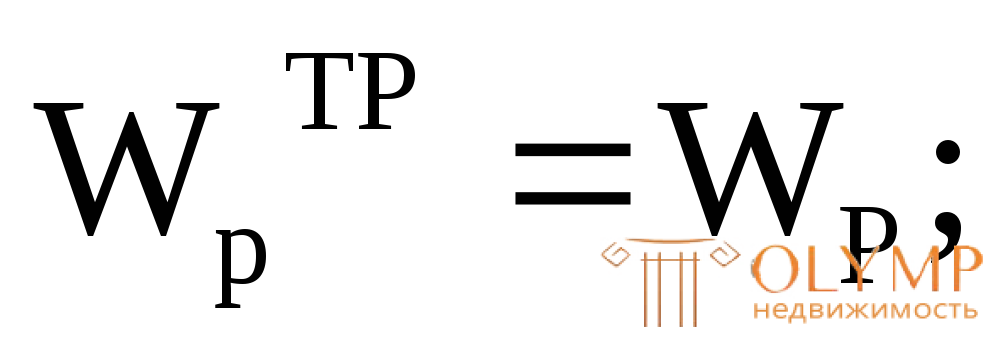

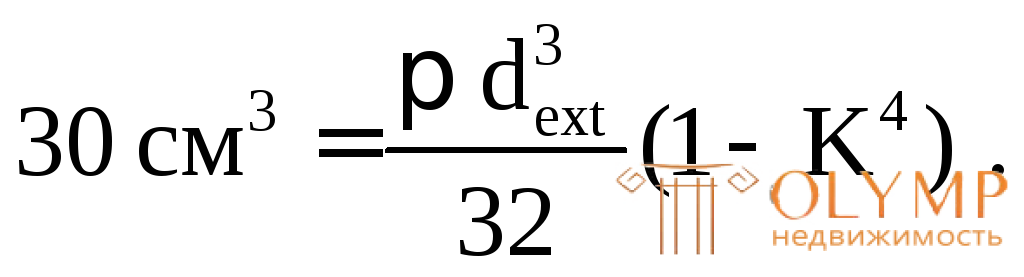
Отсюда при заданном К = 0,8 находим d_ext= 6,37 см.

3. Подбор сечения по условию жесткости. Из условия жесткости (6.15) 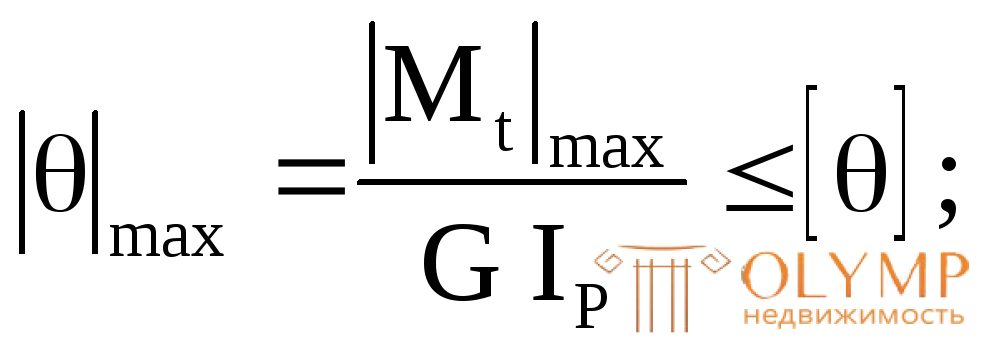определим требуемое значение полярного момента инерции по следующей формуле: 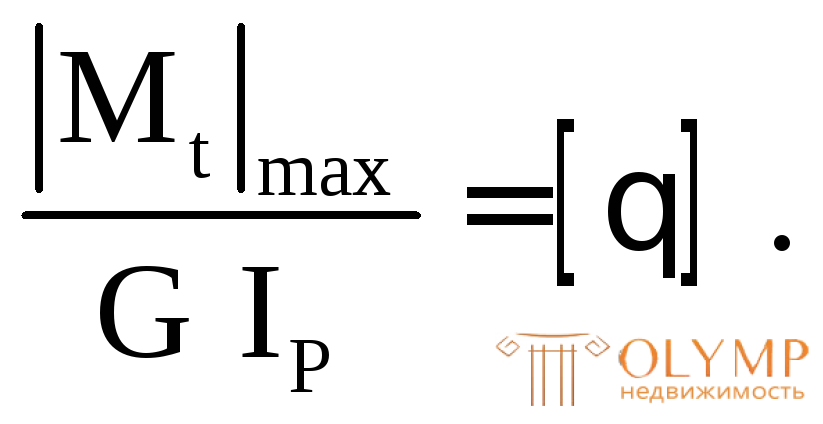Откуда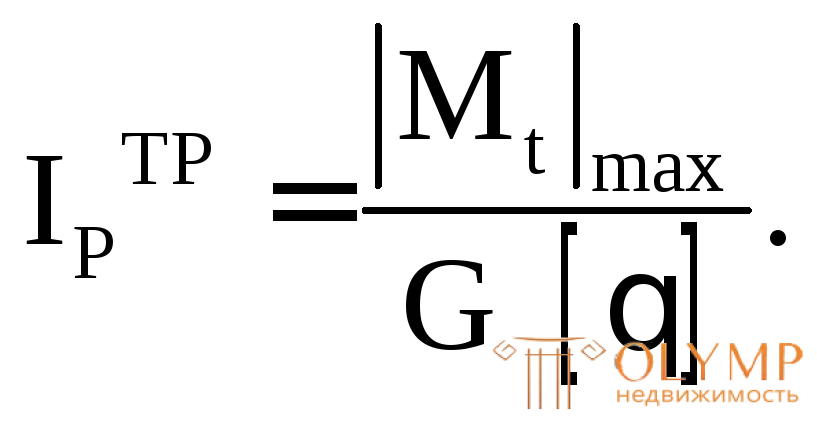

В это соотношение подставляется в радианах, поэтому заданный угол выразим в радианах:

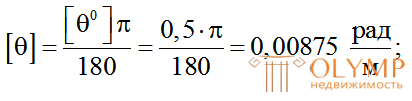
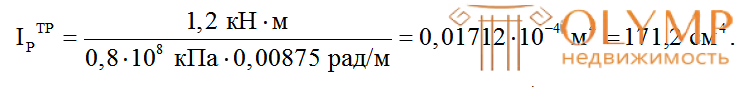
Из условия получим: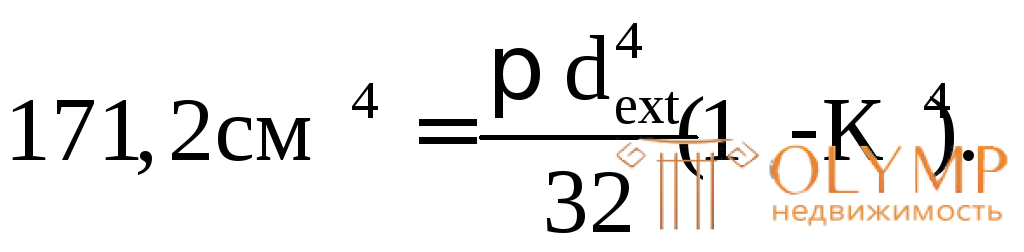

Отсюда определяем d_ext(по условию задачи К = 0,8):

171,2 =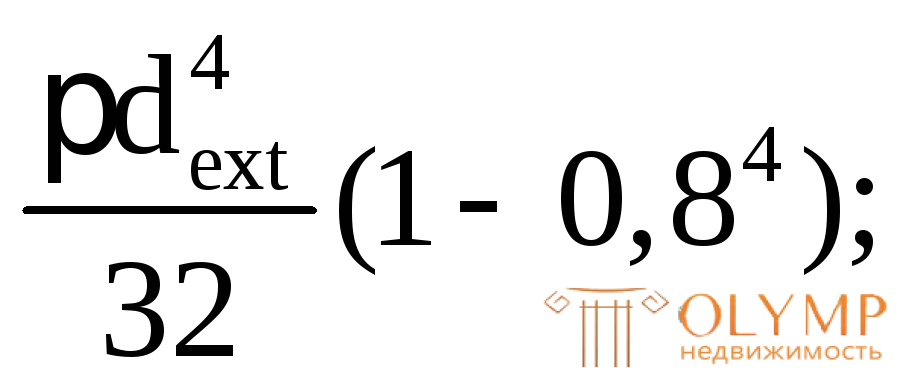

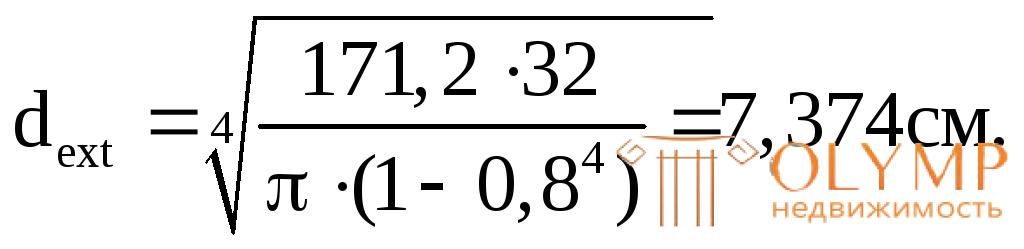
После округления примем d_ext = 7,4, тогда

d_int = 0,8d_ext = 0,87,4 = 5,92 см.

По результатам расчетов на прочность и жесткость видно, что по условию жесткости диаметр бруса требуется больше, чем по условию прочности (7,4 см > 6,37 см).

Окончательно принимаем больший диаметр:

d_ext= 7,4 см,d_int= 5,92 см.

Проверим прочность и жесткость подобранного сечения.

Предварительно определим полярный момент сопротивления и полярный момент инерции подобранного сечения:

Условия прочности и жесткости выполняются.