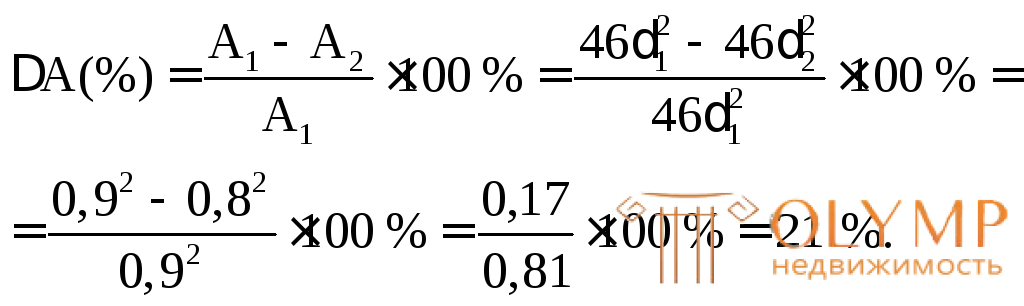
ПРИМЕР 7.1
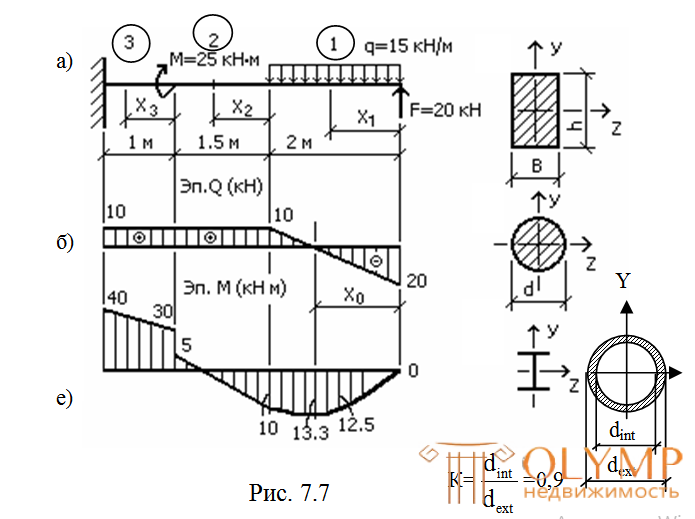
Для балки, изображенной на рис. 7.7а, требуется:
– построить эпюры М и Q;
– подобрать сечение в четырех вариантах (рис. 7.7б, в, г, д) и проверить прочность подобранных сечений по нормальным и касательным напряжениям.
РЕШЕНИЕ
А. Построение эпюр М и Q
1. В пределах грузовых участков 1, 2, 3 (рис. 7.7а) проводим сечения на расстоянии xiот начала каждого участка. При этом рассматриваем правую, свободную от опоры, часть балки, а левую отбрасываем.
Заменяя действие отброшенной части неизвестными
положительными поперечной силой Qi(xi) и изгибающим моментом Мi(xi) и рассматривая равновесие выделенной части балки, находим выражения внутренних усилий на участках.
При построении эпюр М и Qи их проверке используем дифференциальные зависимости Д.И. Журавского между М,Qиq:
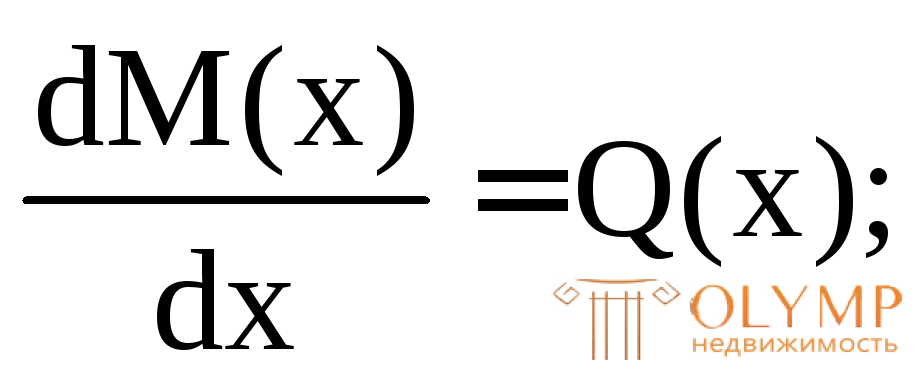
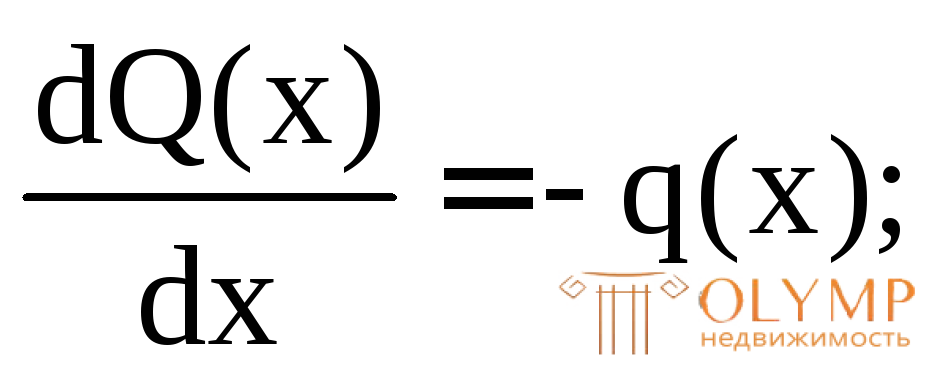
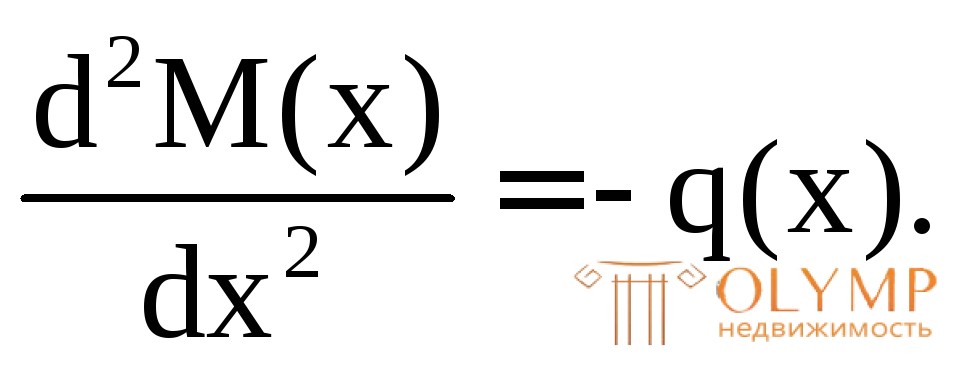 (7.17)
(7.17)
В зависимостях (7.11) перед q ставится знак "минус", если распределенная нагрузка направлена вниз.
1-й грузовой участок (рис. 7.8) 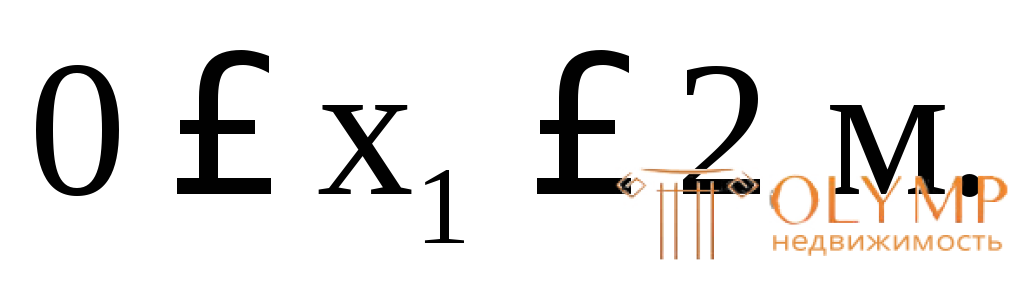
 Составим уравнения равновесия для 1-го участка.
Составим уравнения равновесия для 1-го участка.
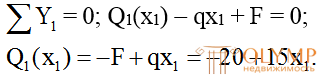
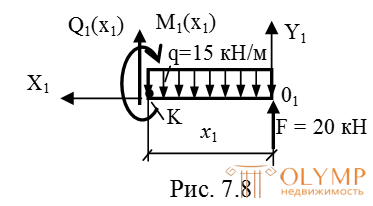
Так какQ1(x1) – линейная функция, то для построения эпюры Q на этом участке достаточно рассмотреть два сечения:
х1= 0 м,Q1(0) = – 20 кН;
х1= 2,0 м,Q1(2) = 10 кН.
Строим эпюру Q из которой видно (см. рис. 7.7е), что на первом участке эпюра поперечных сил имеет нулевую ординату. В соответствии с дифференциальной зависимостью (7.17) между М и Q (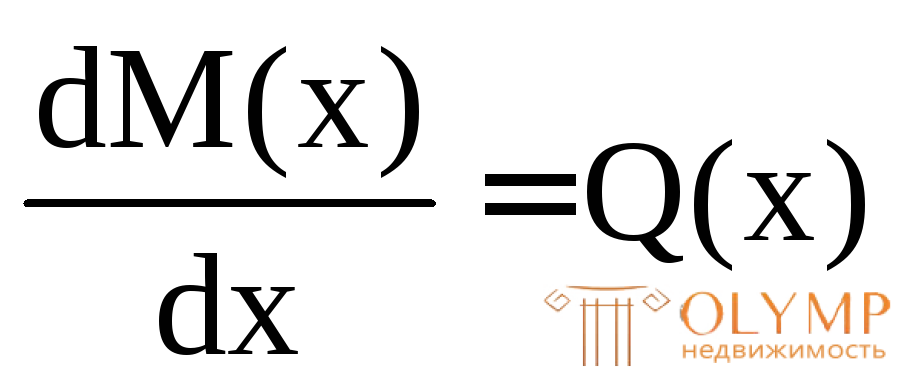 ) эпюра изгибающих моментов на этом участке будет иметь экстремум.
) эпюра изгибающих моментов на этом участке будет иметь экстремум.
Приравнивая Q1(х1) к нулю при х1= х0, получим:
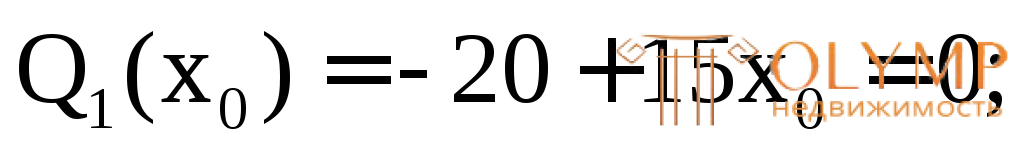
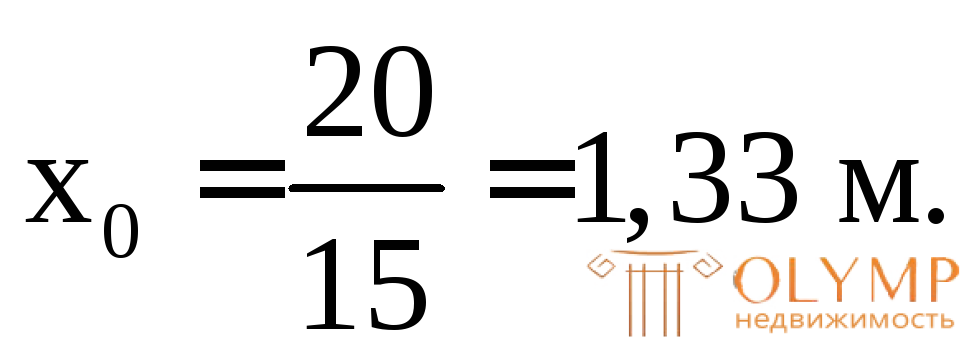
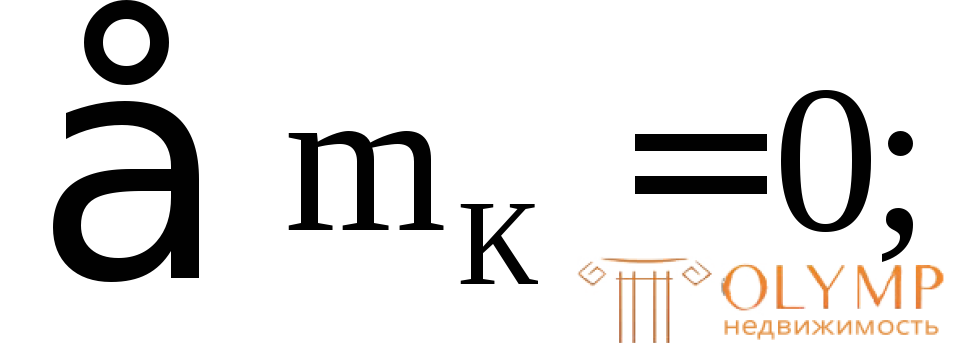 –М1(х1) – q
–М1(х1) – q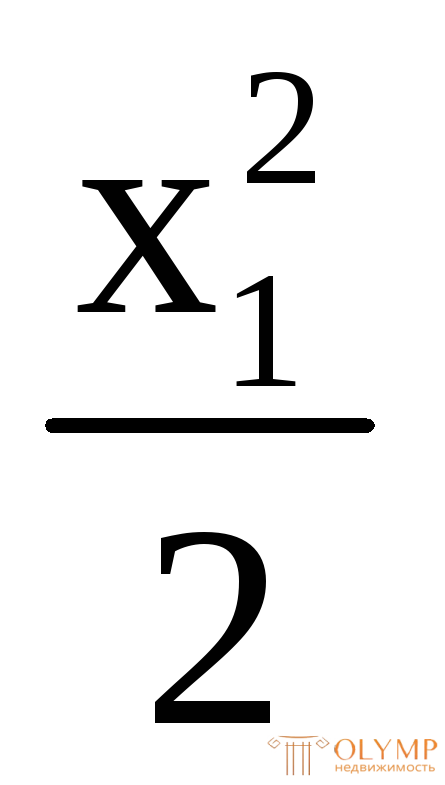 +Fx1= 0;
+Fx1= 0;
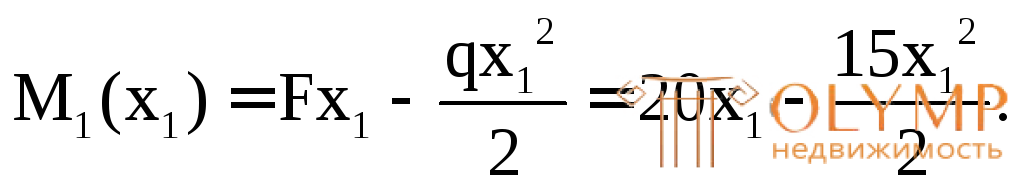
Функция М1(х1) – квадратичная, поэтому для построения графика этой функции на данном участке (эпюры М), находим не менее трех значений изгибающего момента:
х1= 0 м, М1(0) = 0 кНм;
х1= х1= 1,33 м, М1(х0) =Mextr= 13,3 кНм;
х1= 2,0 м, М1(2) = 10 кНм.
По найденным значениям строим эпюру М на первом участке под эпюрой поперечных сил. Изгибающие моменты откладываем со стороны растянутых волокон, т.е. "плюс" – вниз (растягиваются нижние волокна), "минус" – вверх (растягиваются верхние волокна) см. (рис. 7.7е, ж).
Аналогично построим эпюры на 2-м и 3-м грузовых участках:
2-й участок (рис. 7.9): 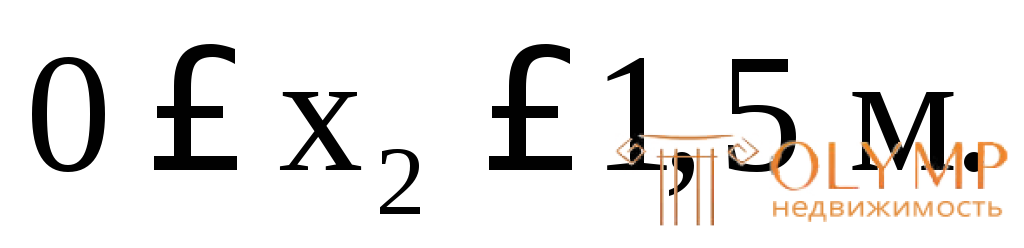
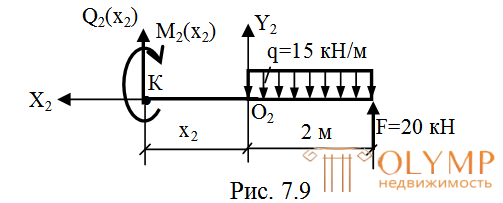
 = 0;Q2(x) –q
= 0;Q2(x) –q 2 +F= 0;
2 +F= 0;
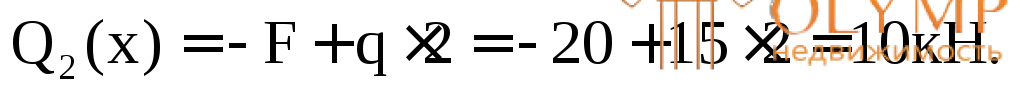
Эпюра Qпостоянна по длине данного участка.
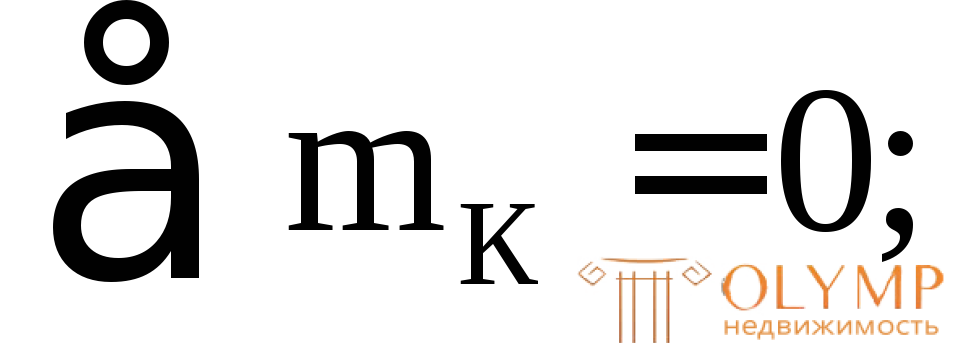 – М2 (х2) – q
– М2 (х2) – q 2 (х2+
2 (х2+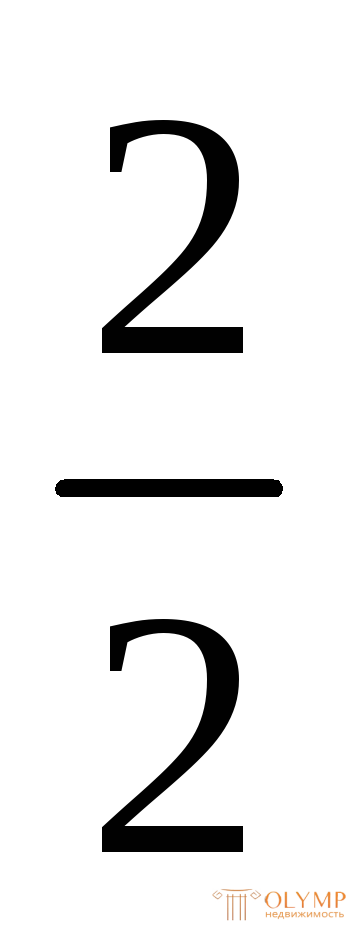 ) +F
) +F (x2+ 2) = 0;
(x2+ 2) = 0;
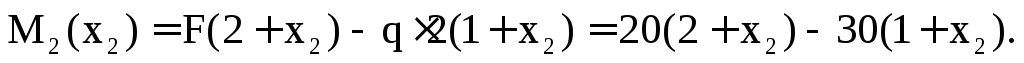
Изгибающий момент на данном участке изменяется по линейному закону:
х2= 0 м, 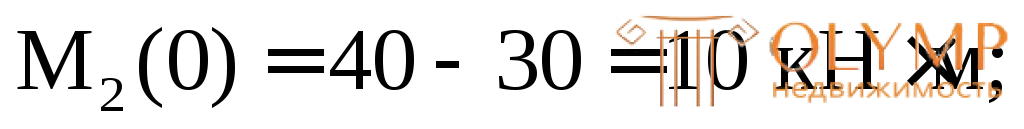
х2= 1,5 м,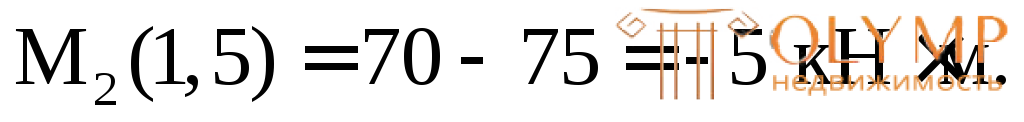
3-й участок (рис. 7.10): 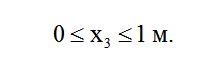
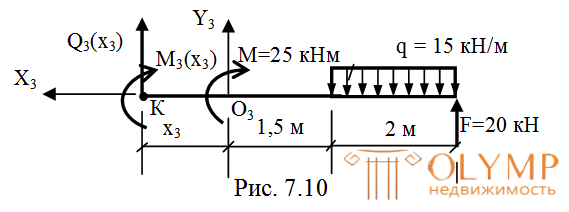
Рассматривая 3-й участок также вырежем правую часть балки. Начало локальной системы координат поместим в начале 3-го участка.
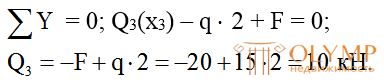
Эпюра Qпостоянна по длине участка.
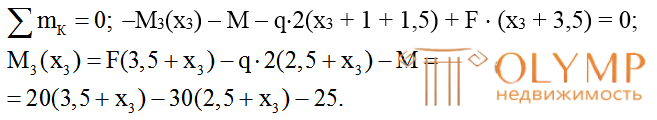
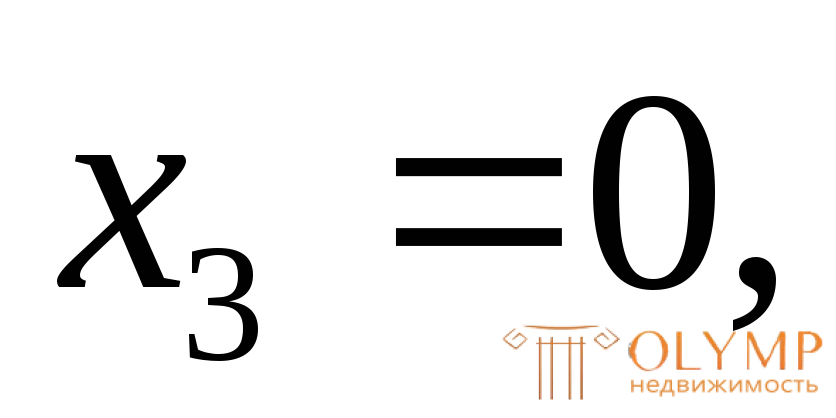
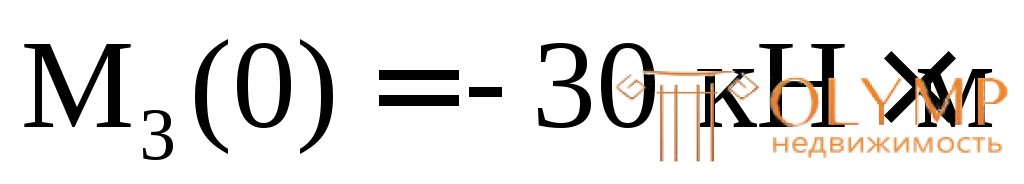 (знак "минус" означает, что растягиваются верхние волокна);
(знак "минус" означает, что растягиваются верхние волокна);
х3= 1 м,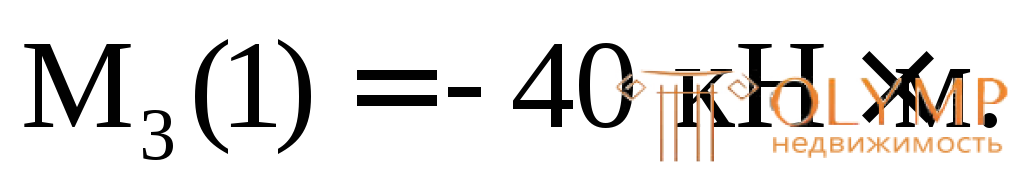
Эпюры М и Q, построенные по результатам расчётов, показаны на рис. 7.7е, ж.
Б. Подбор сечения
Из эпюр М и Q имеем: 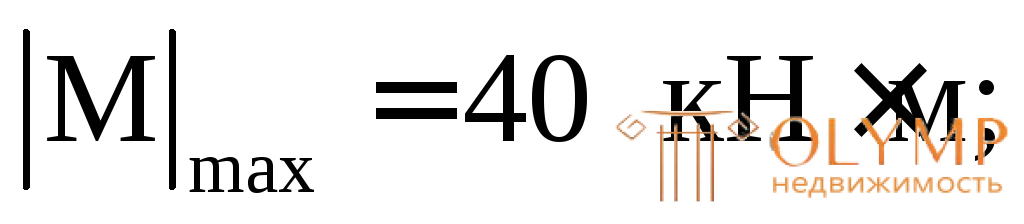
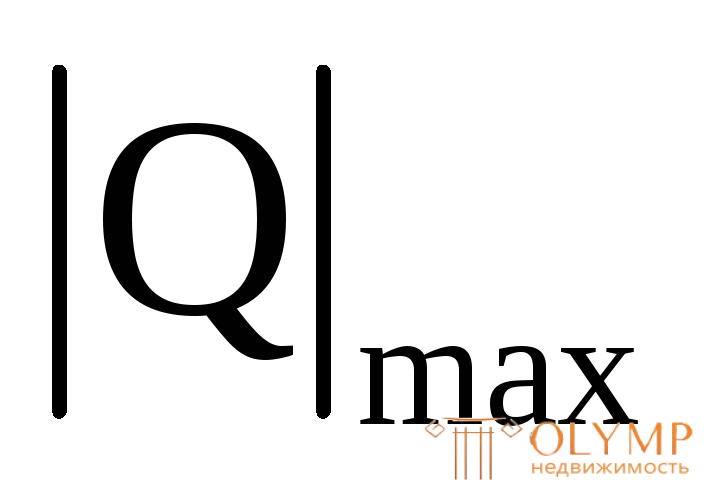 = 20 кН.
= 20 кН.
1. Балка прямоугольного сечения(см. рис. 7.7б):
R= 10 МПа,Rs= 5 МПа,h= 4b.
Из условия прочности (7.2) определим требуемую величину осевого момента сопротивления при 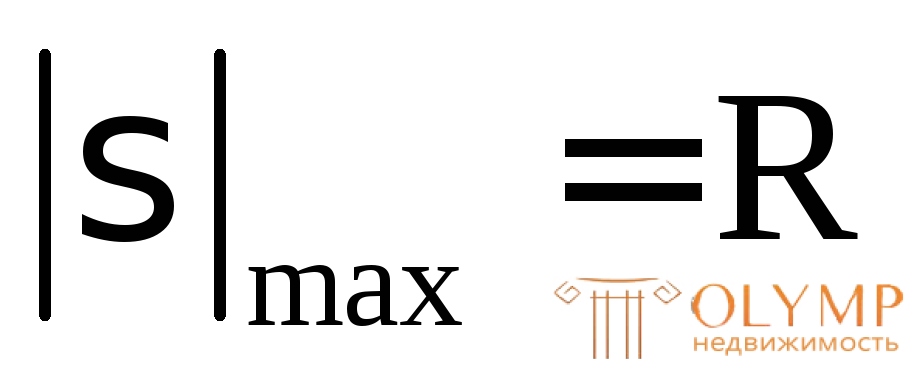 :
:
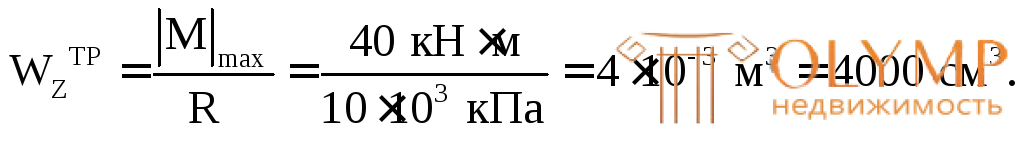
Осевой момент сопротивления для прямоугольного сечения при заданных соотношениях сторон определится по формуле:
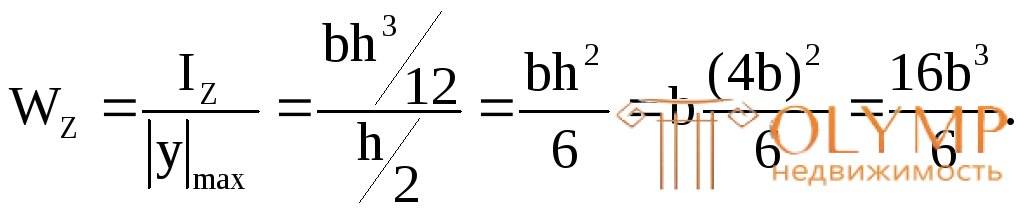
Приравняем 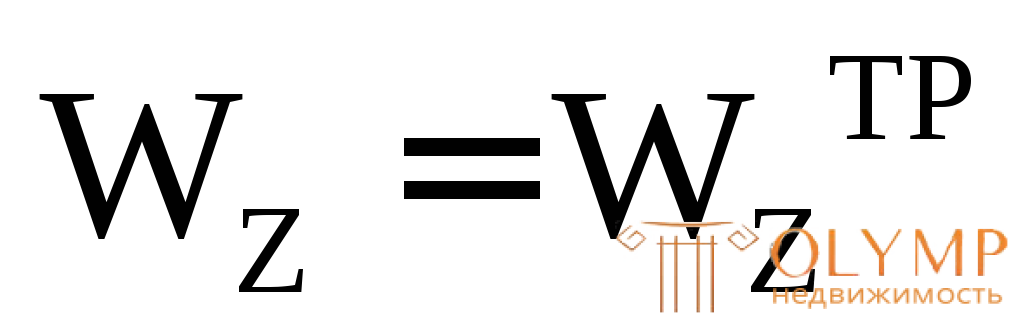 и найдем размер сечения b:
и найдем размер сечения b:
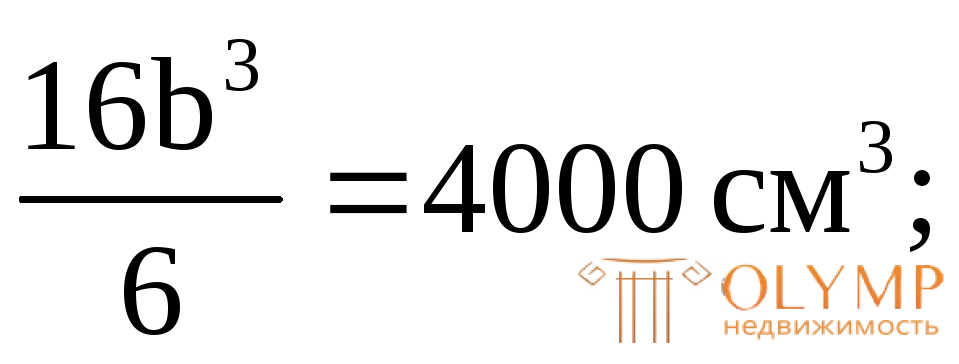
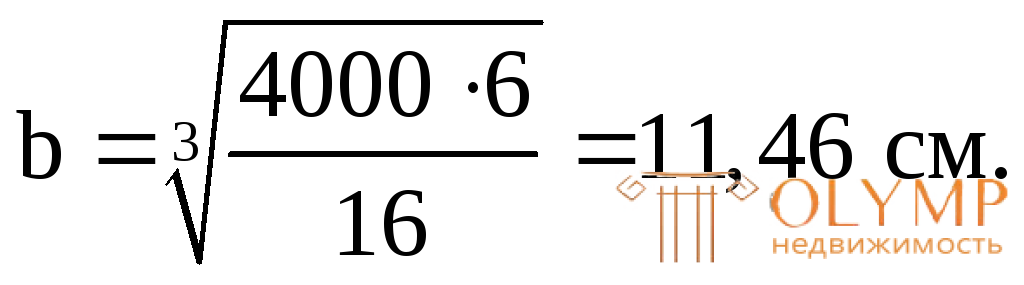
Округляя в большую сторону, примем:
b= 11,5 см,h= 4b= 4 11,5 = 46 см.
11,5 = 46 см.
Проверим прочность подобранного сечения по нормальным и касательным напряжениям.
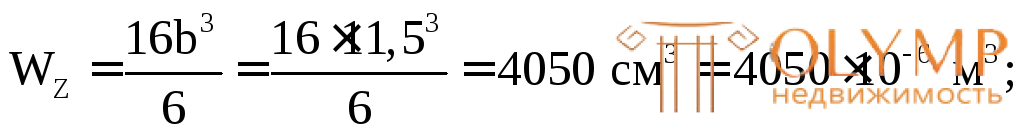
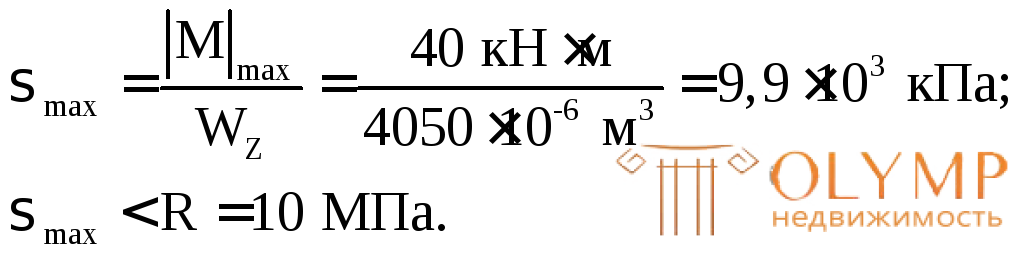
Прочность по нормальным напряжениям обеспечена. Недонапряжение в 1 % объясняется округлением размера сечения bв большую сторону.
Для проверки прочности по касательным напряжениям используем формулу (7.11):
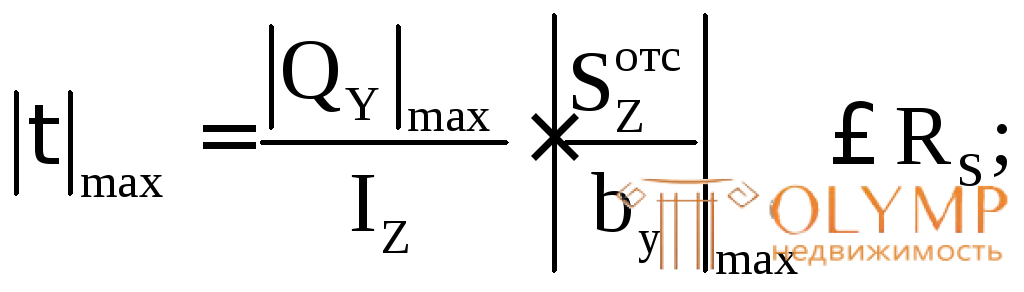
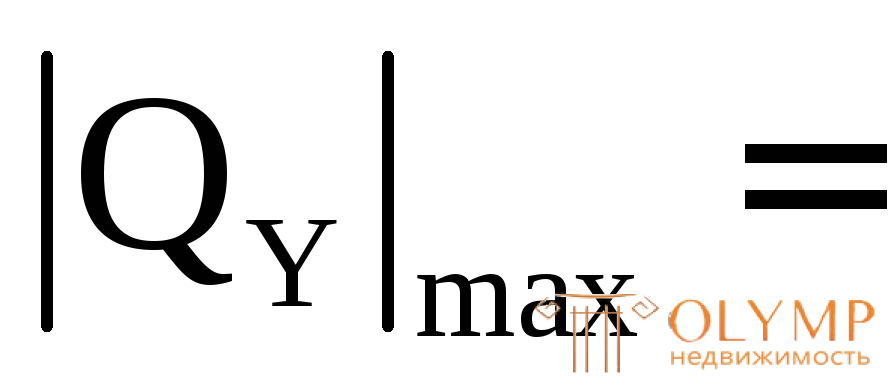 20 кН, (из эпюры Q);
20 кН, (из эпюры Q);
I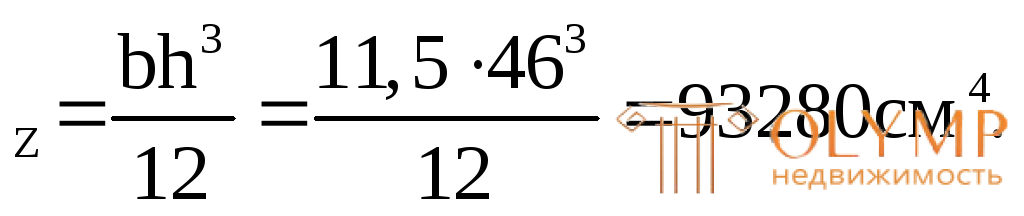
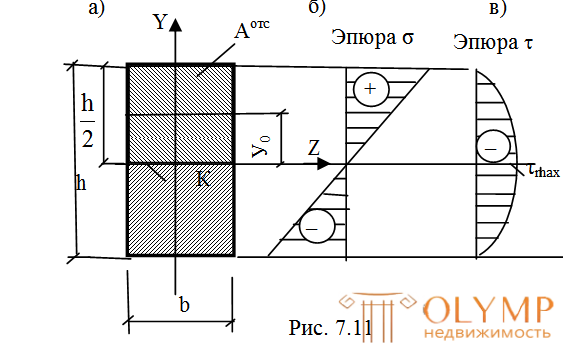
Наибольшие касательные напряжения для прямоугольного сечения возникают в точках, лежащих на центральной оси Z, так какS для полусечения (отсечение проводится через точку К, находящуюся на центральной осиZ) имеет максимальное значение (рис. 7.11в):
для полусечения (отсечение проводится через точку К, находящуюся на центральной осиZ) имеет максимальное значение (рис. 7.11в):
S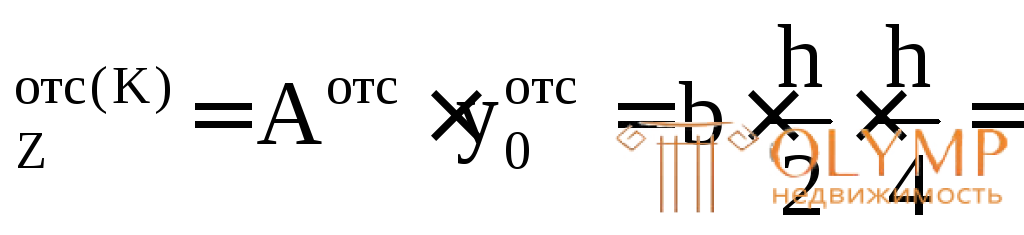 11,5
11,5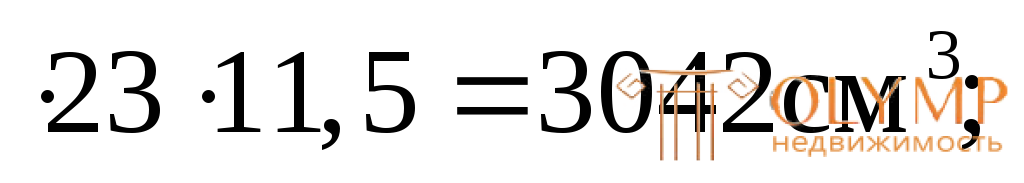
b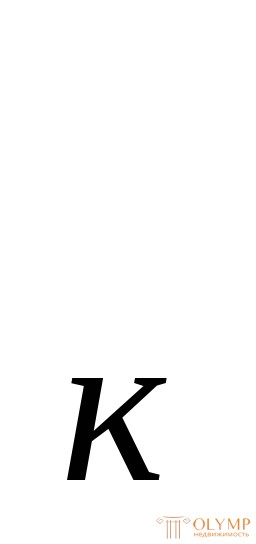 = b = 11,5 см. Аотс = b
= b = 11,5 см. Аотс = b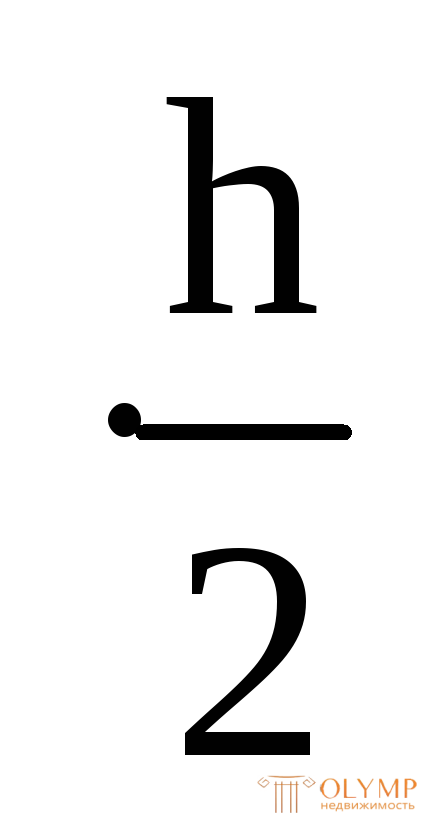 ; y
; y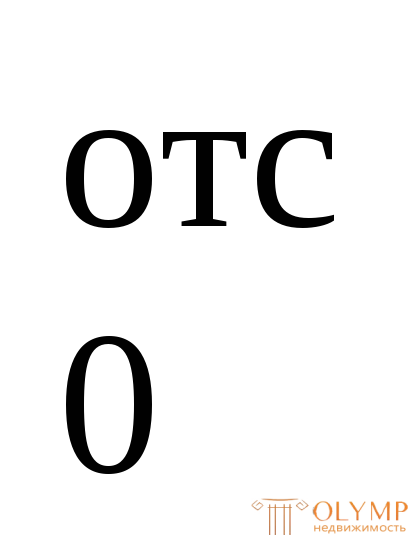 =
=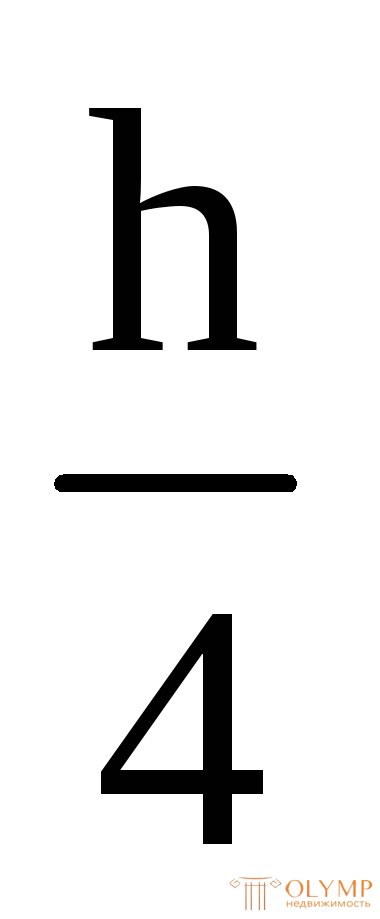 .
.
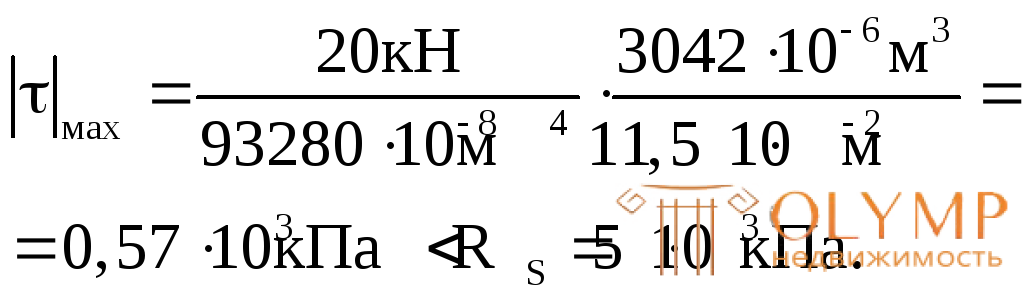

Прочность по касательным напряжениям обеспечена с большим запасом.
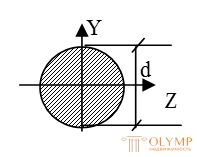
2. Балка сплошного круглого сечения, материал – дерево,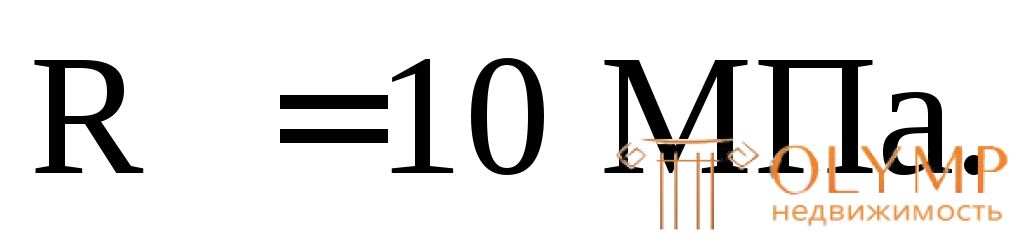
Требуемый осевой момент сопротивления берем из предыдущего расчета, так как он не зависит от формы сечения 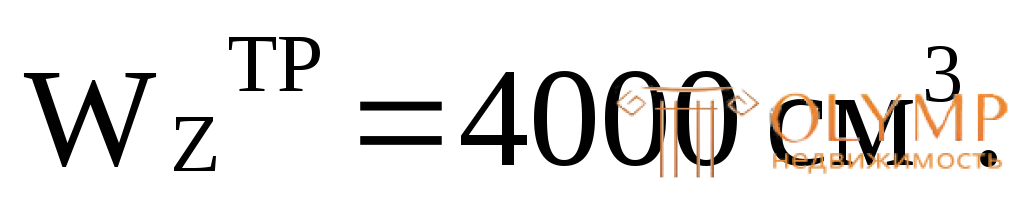
Осевой момент сопротивления для круглого сечения:
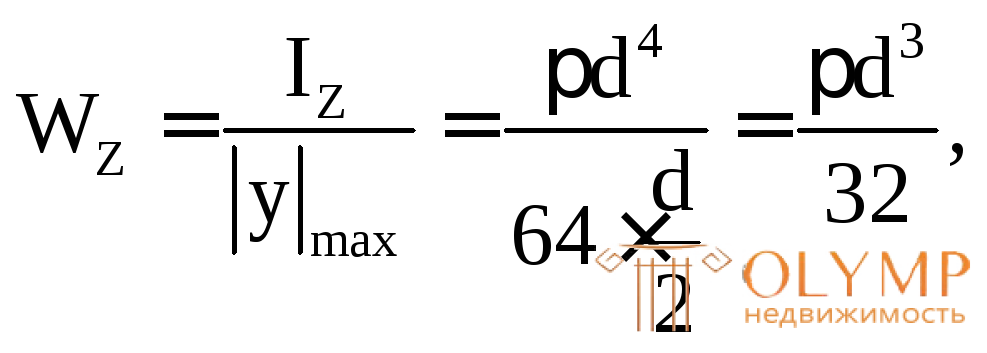 где
где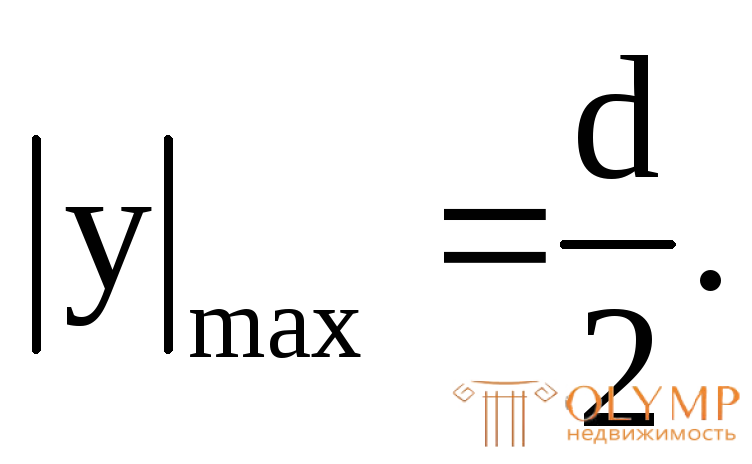
Из условия 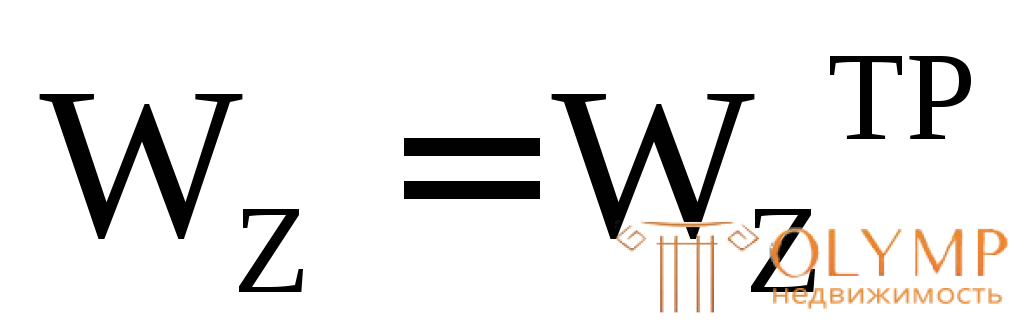 имеем:
имеем:
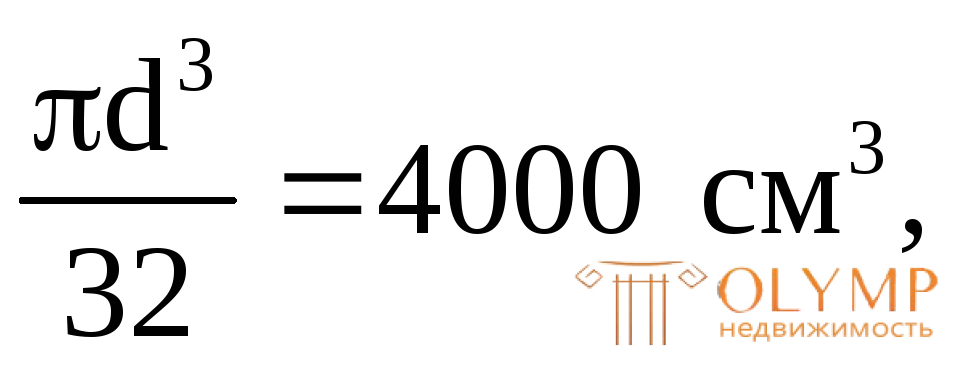 отсюда –
отсюда –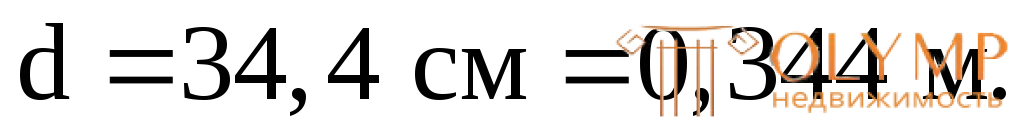
Округляя, примем d = 0,35 м.
Проверим прочность подобранного сечения по нормальным напряжениям:
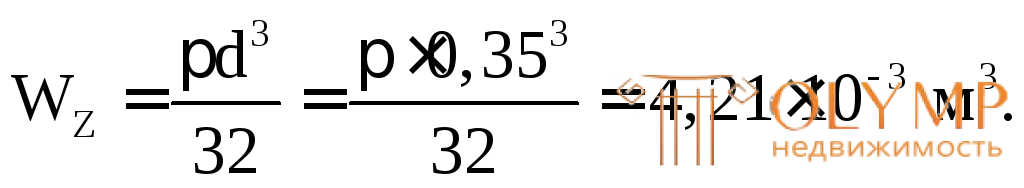
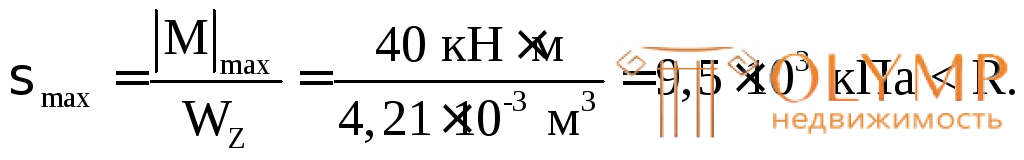
Прочность балки по нормальным напряжениям обеспечена. Небольшое недонапряжение (–5 %) объясняется округлением диаметра в большую сторону.
Наибольшая ширина данного сечения dнаходится на центральной оси, значит максимальные касательные напряжения будут небольшими, поэтому для данного сечения проверку по касательным напряжениям можно не производить.
3. Балка из прокатного двутавра (см. рис. 7.7г).
Из условия прочности по нормальным напряжениям определяем требуемое значение осевого момента сопротивления:
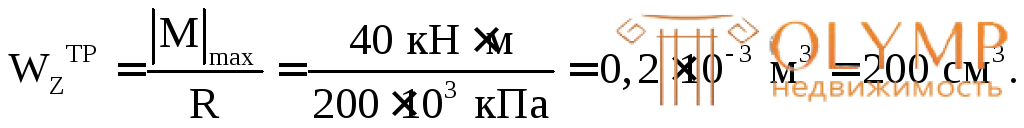
Из таблицы сортаментов по ГОСТ 8239-89 для стального проката находим двутавр, имеющий близкий к требуемому осевой момент сопротивления:
Двутавр № 20, 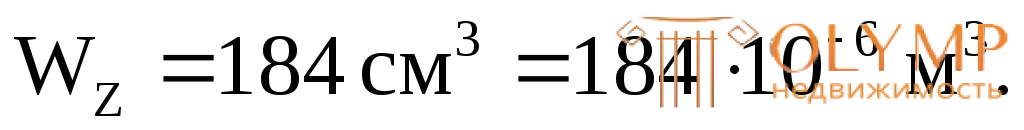
Проверим прочность этого двутавра:
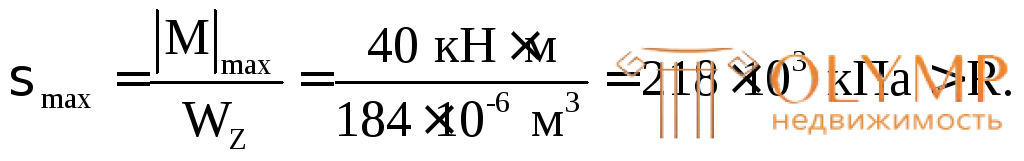
Определим процент перенапряжения.
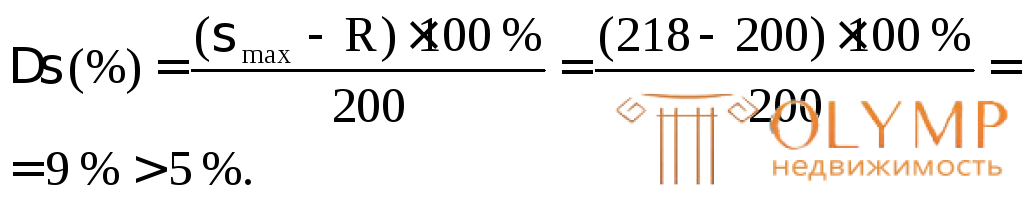
Такая величина перенапряжения считается недопустимой, поэтому проверим прочность двутавра № 22.
Для этого двутавра из сортамента имеем 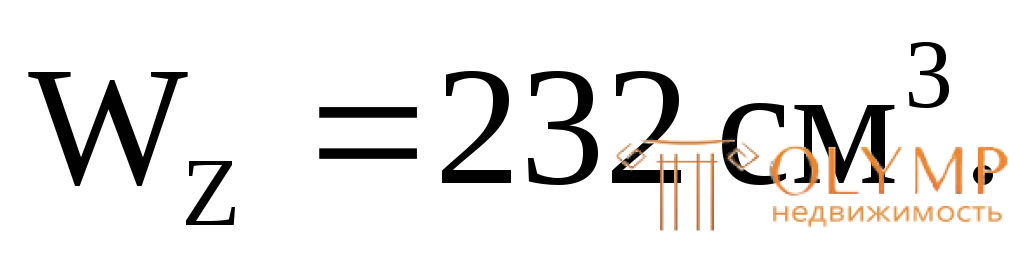
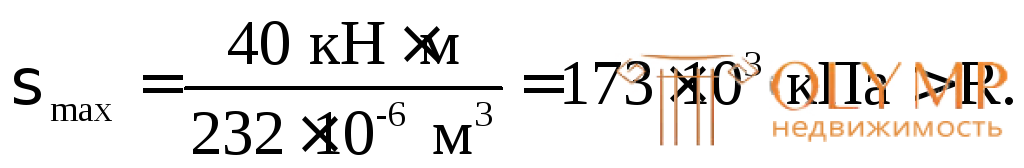
Имеет место недонапряжение
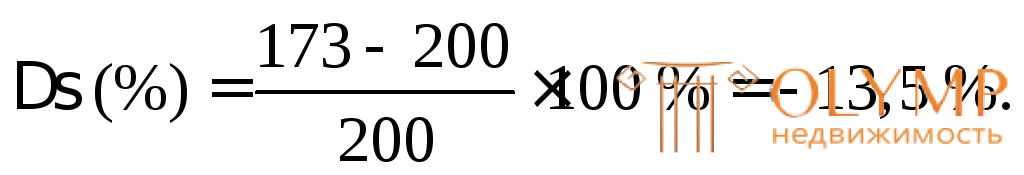
Окончательно выбираем двутавр № 22.
Проверим прочность подобранного сечения по касательным напряжениям.
Наибольшие касательные напряжения будут в точках сечения, лежащих на центральной оси, так как статический момент полусечения имеет максимальное значение, а толщина в этом месте – минимальная.
Для двутавра № 22 из таблицы сортаментов для прокатных двутавров (ГОСТ 8239-89) получаем:
I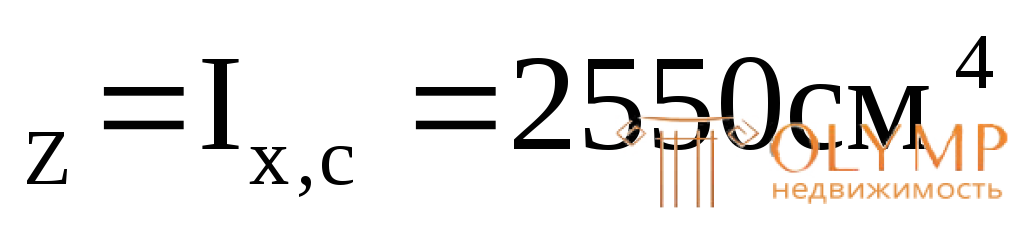 ;
;
bК=sc= 5,4 мм = 0,54 см;
S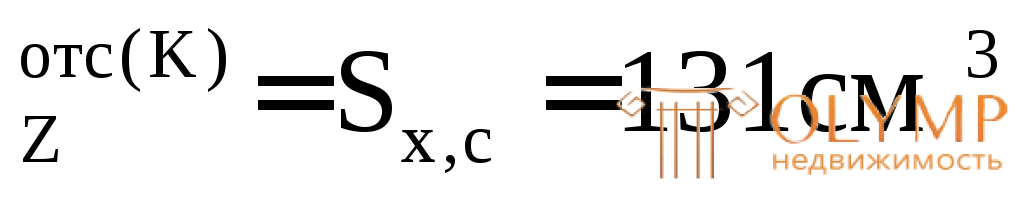 – статический момент полусечения.
– статический момент полусечения.
Тогда
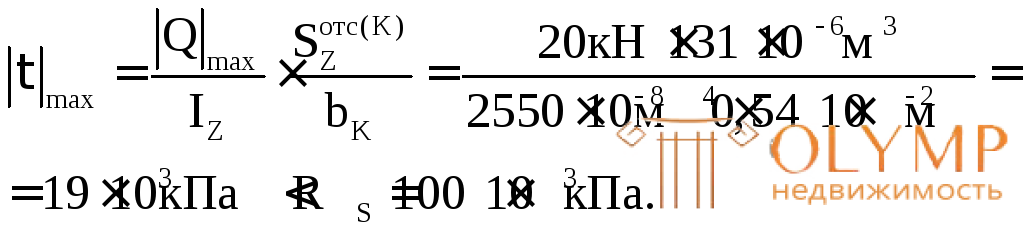
Прочность балки по касательным напряжениям обеспечена с большим запасом.
4. Балка из стальной трубы (см. рис. 7.7д)
R= 200 МПа;RS= 100 МПа; 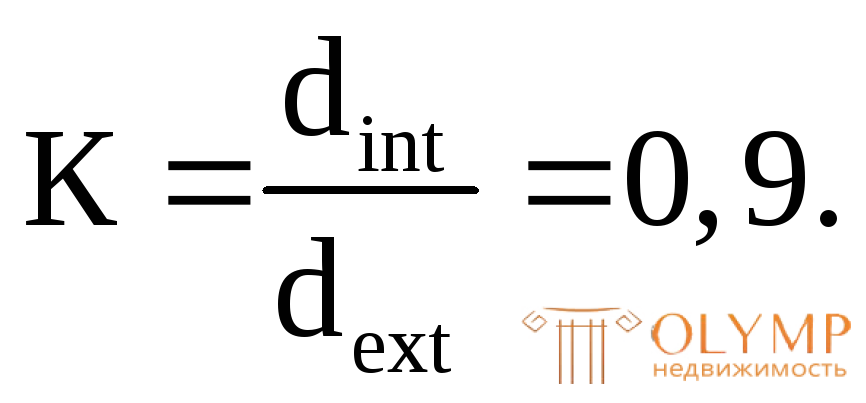
Из предыдущего, третьего пункта, имеем:
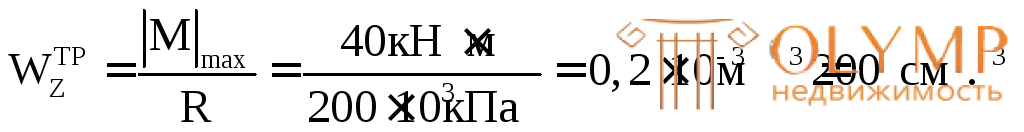
Для кольцевого поперечного сечения:
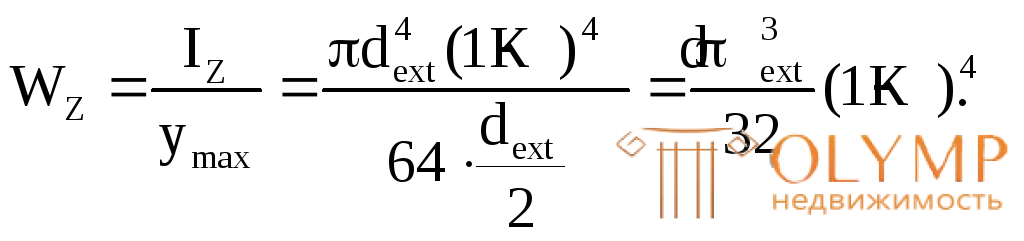
Из условия: WZ=W определяем наружный диаметрdext:
определяем наружный диаметрdext:
200 см3=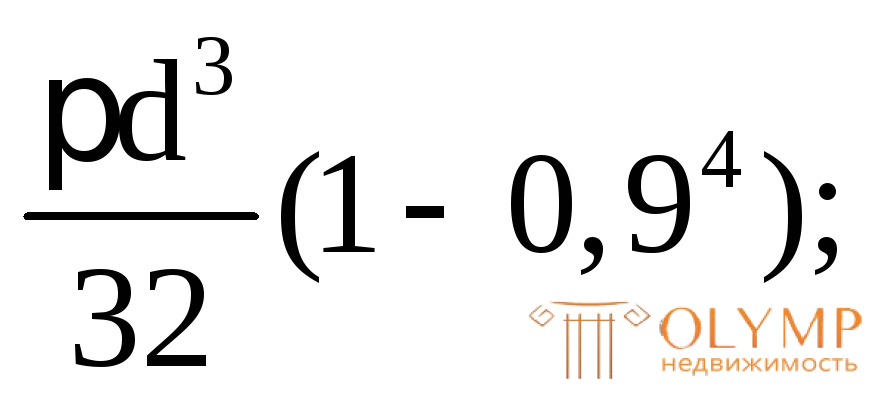
dext=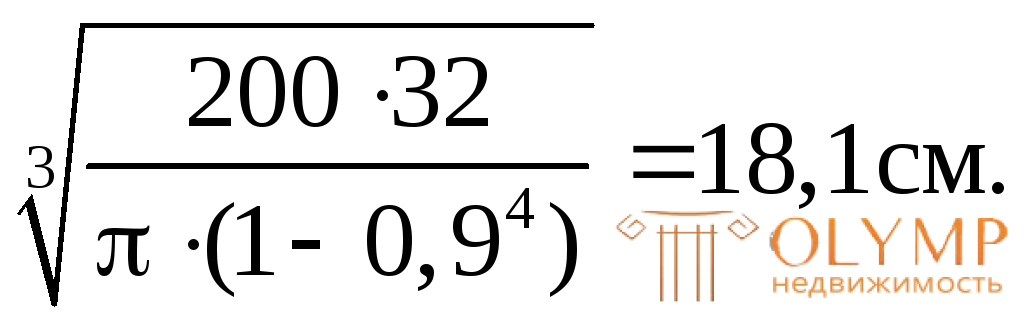
Округляя, примем dext= 18 см;dint= 0,9dext= 0,9 18 = = 16,2 см.
18 = = 16,2 см.
Проверим подобранное сечение по нормальным и касательным напряжениям:
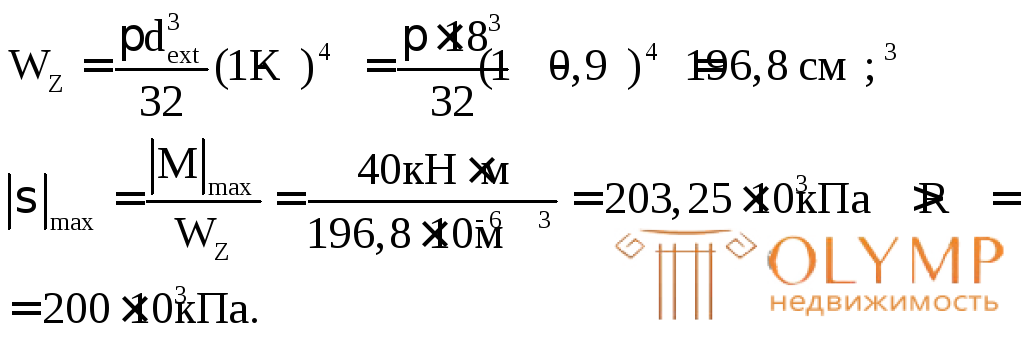
Относительная величина перенапряжения составляет:
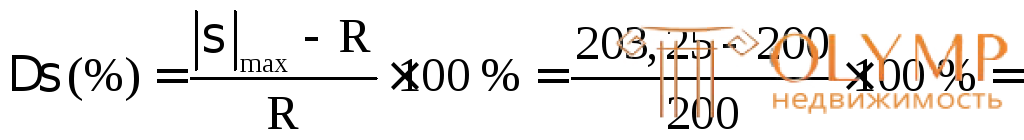
= 1,6 % < 5 %, что допустимо и объясняется округлением требуемого диаметра в меньшую сторону.
Проверяем прочность поперечного сечения по касательным напряжениям. Опасной является точка, лежащая на центральной оси Z, так как для этой точки статический момент полусечения достигает максимального значения, а ширина сечения имеет минимальную величину. Для проверки прочности используем формулу (7.11):
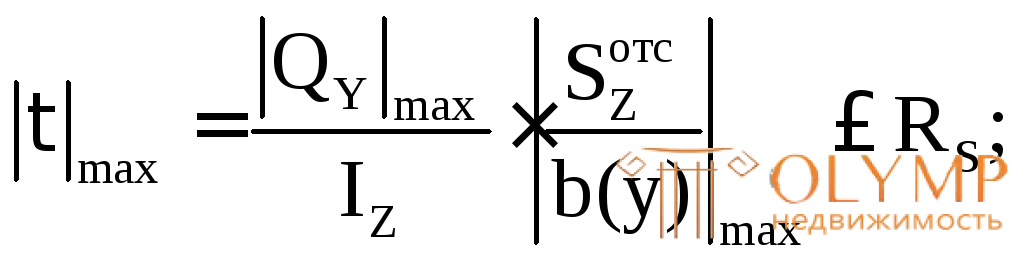
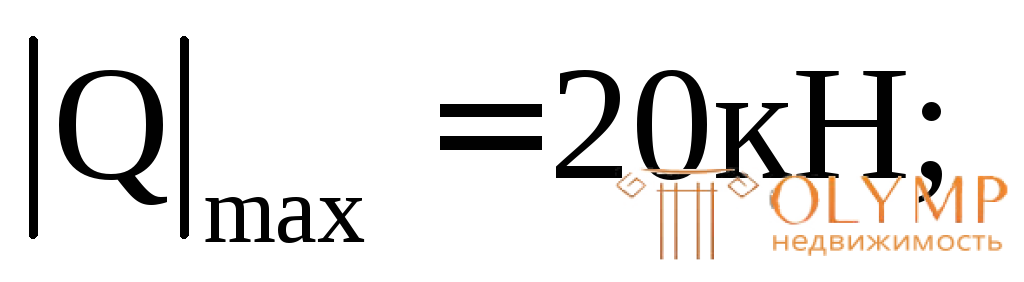
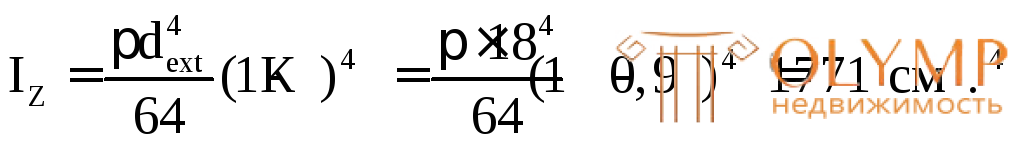
Ширина сечения на уровне центральной оси bК определится как разность диаметров: bК=dext –dint= 18 – 16,2 = 1,8 см.
Статический момент отсеченной части сечения выше центральной оси Zопределим как разность статических моментов большего и меньшего полукругов:
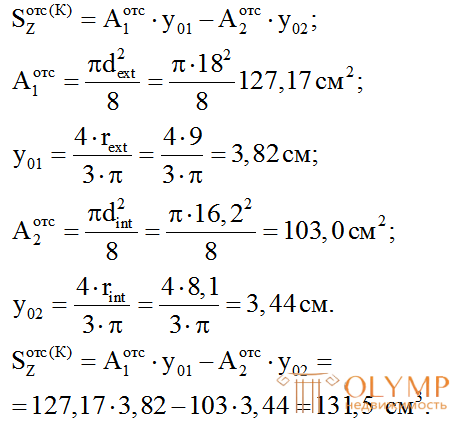
Максимальное касательное напряжение составляет:
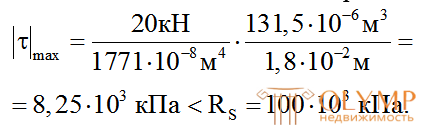
Условие прочности по касательным напряжениям выполняется с большим запасом.
ПРИМЕР 7.2
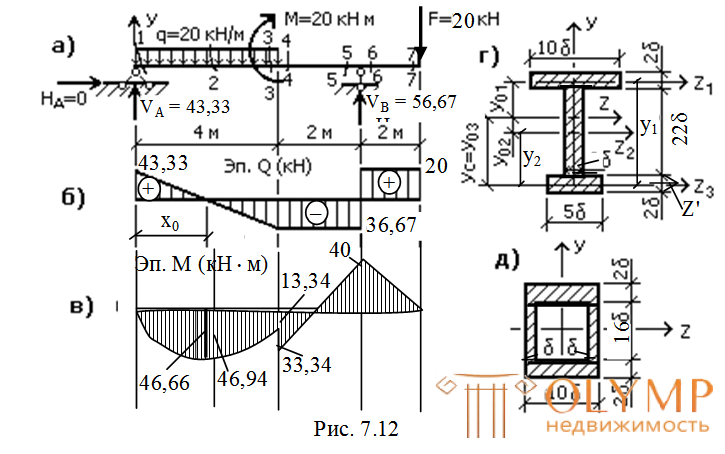
Для балки, изображенной на рис. 7.12а, требуется:
– построить эпюры М и Q;
– подобрать размеры стальных составных сечений в двух вариантах (по рис. 7.12г, д).
РЕШЕНИЕ
А. Построение эпюр М и Q
Определяем реакции опор
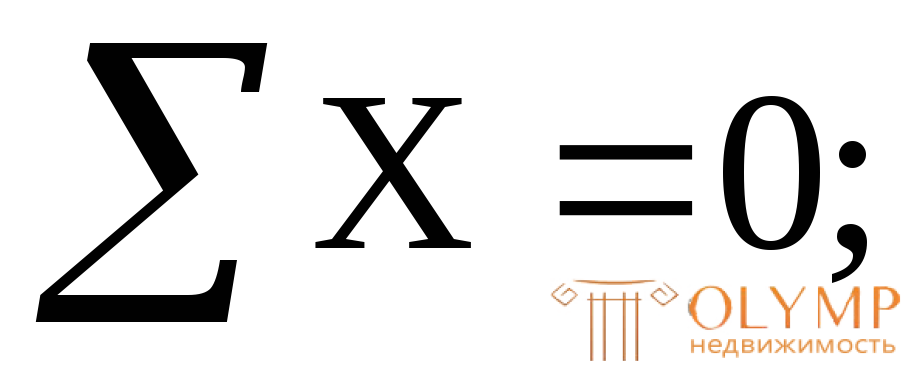 НА= 0;
НА= 0;

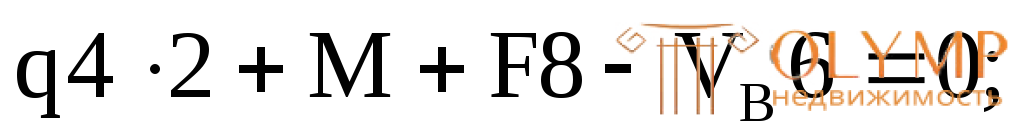
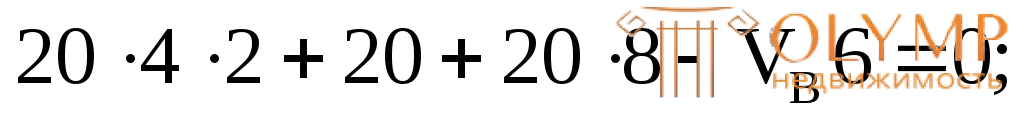 VB= 56,67 кН;
VB= 56,67 кН;
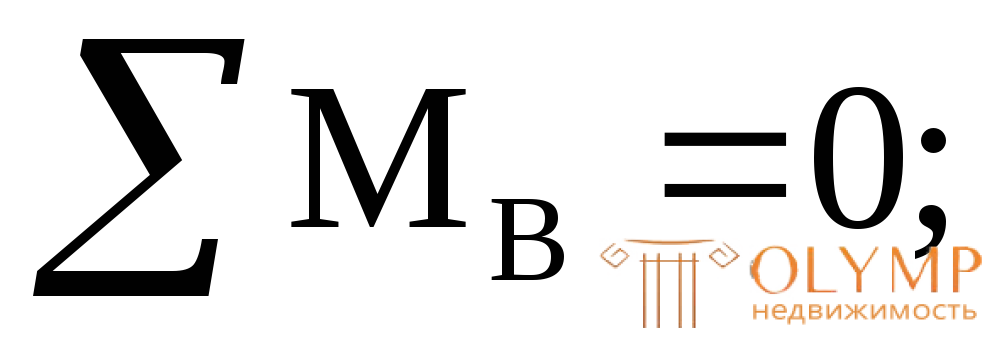
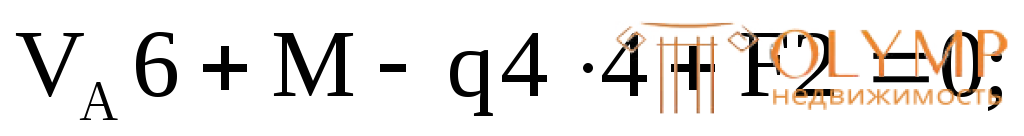
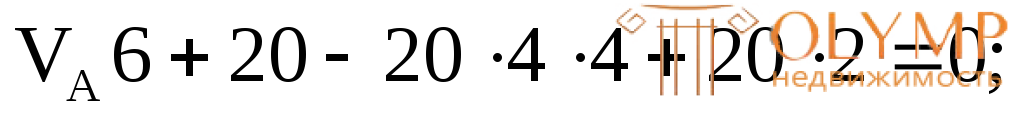
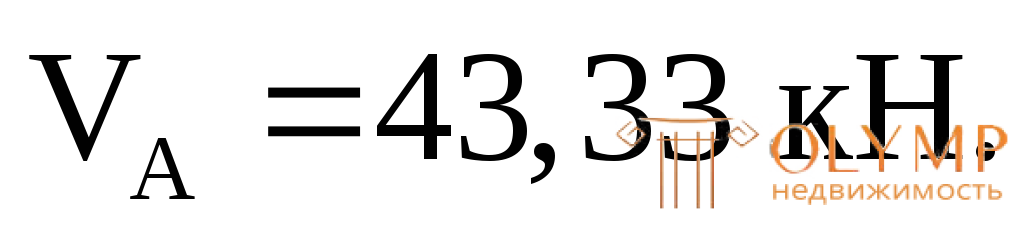
Проверка: 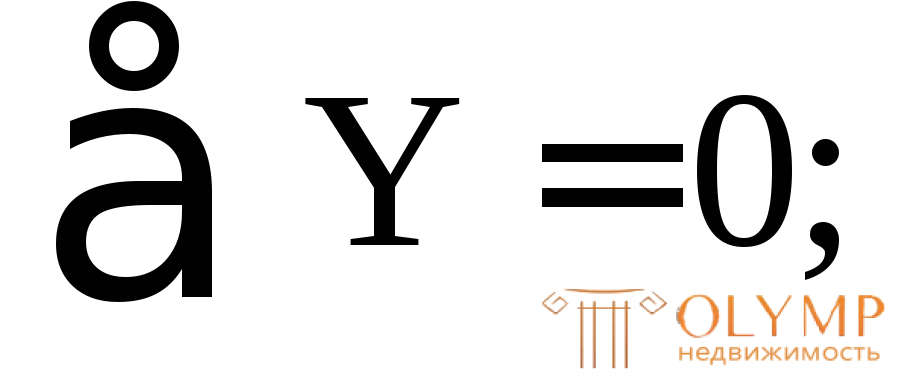
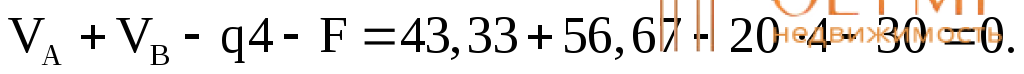
В отличие от предыдущего примера определим изгибающие моменты и поперечные силы в отдельных сечениях балки без составления функций для М и Q, используя только приведенные ранее (п. 7.1, стр. 122) рабочие правила и правила знаков.
Сечения проведем бесконечно близко в начале и в конце грузовых участков, на которых отсутствует распределенная нагрузка q. Дополнительное сечение проведем по середине участка, где имеетсяq(рис. 7.12 а).
Вычислим значения Q и М в этих сечениях. Для сечений 1–1,2–2, 3–3 будем рассматривать левую отсеченную часть, а для остальных – правую часть.
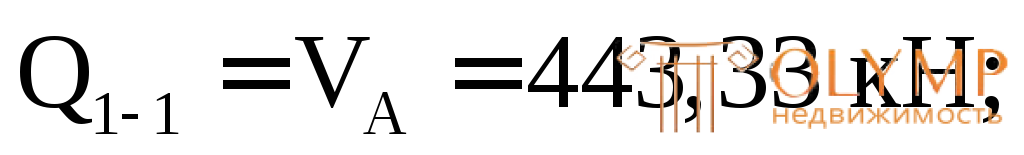
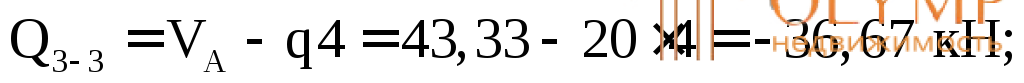
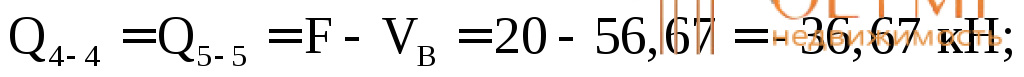
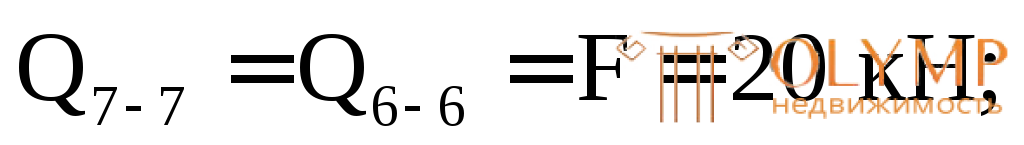
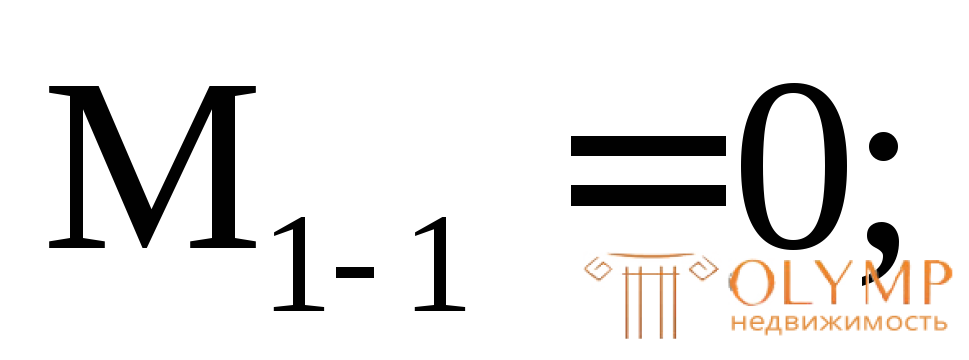
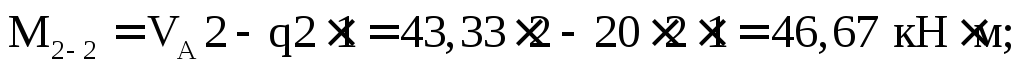
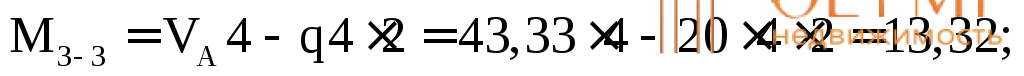
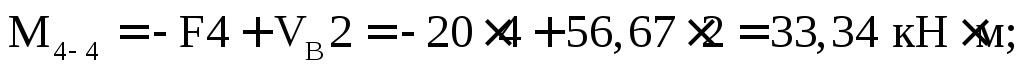
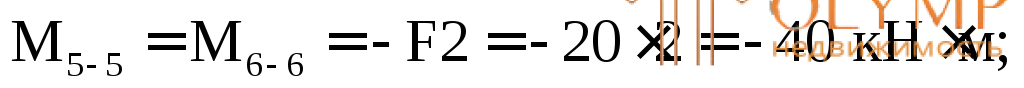
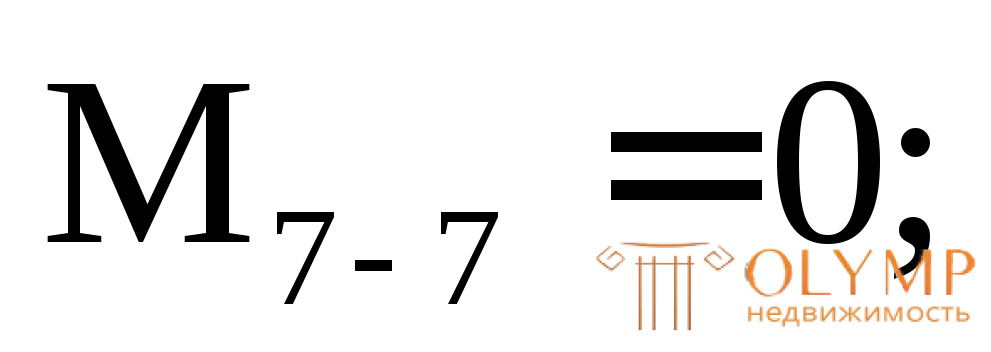
По полученным результатам строим эпюры М и Q(рис. 7.12б, в).
Эпюру М строим со стороны растянутых волокон, т.е. значения М со знаком "минус" откладываем вверх. Из эпюры Qвидно, что экстремальное значение изгибающего момента на 1-м грузовом участке будет в сечении на расстоянии х0, т.е. там, где Q(х0) = 0. Из этого условия находим величину х0:
Q(х0) = VA –qx0= 43,33 – 20x0= 0;x0=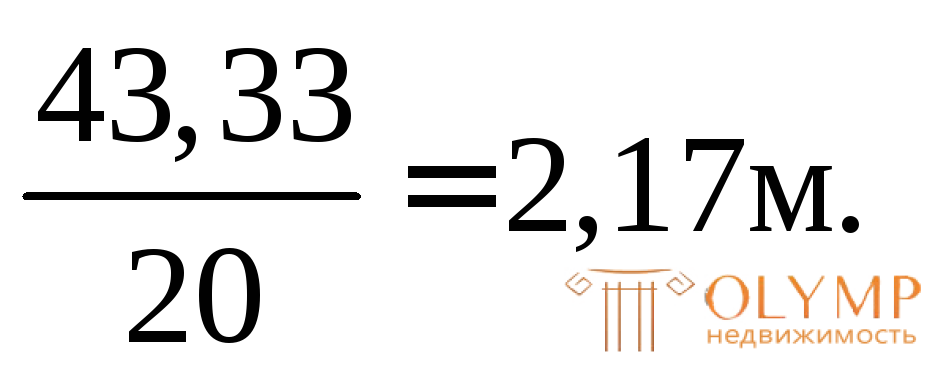
Вычисляем в этом сечении величину Мэкстр:
Мэкстр.= М(х = х0) = 43,33 2,17–20
2,17–20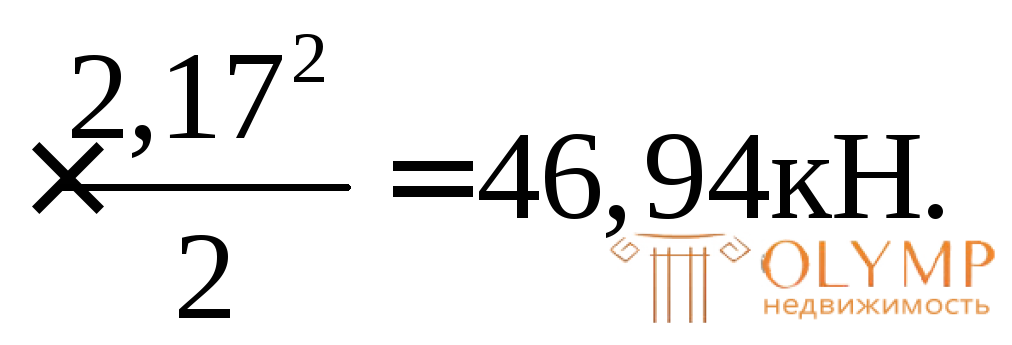
При анализе правильности эпюр с учетом дифференциальных зависимостей между М, Qиq(7.13) замечаем:
– на эпюре М имеется скачок там, где приложен внешний сосредоточенный момент 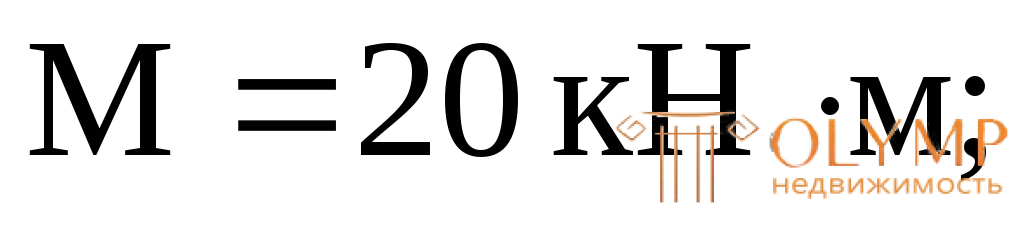
– на эпюре Q имеются скачки в сечениях, где приложены внешние сосредоточенные силы, в том числе и опорные реакции;
– на участках, где отсутствует q, эпюра моментов изменяется по линейному закону, а эпюра Q постоянна;
– на участке, где имеется равномерно распределенная нагрузка интенсивностью q, эпюра М меняется по закону квадратной параболы, выпуклостью в сторону действия q, а эпюра Q – по линейному закону. Тангенс угла наклона этой прямой к продольной оси балки равен интенсивности нагрузки q.
Б. Подбор сечения балки
1. Вариант сечения по рис. 7.12г
R= 200 103кПа; RS= 100
103кПа; RS= 100 103кПа.
103кПа.
А. Из условия прочности по нормальным напряжениям определяемтребуемую величину осевого момента сопротивления.
Из эпюры изгибающих моментов получаем |M|max = = 46,94 кНм.
Допускаем, 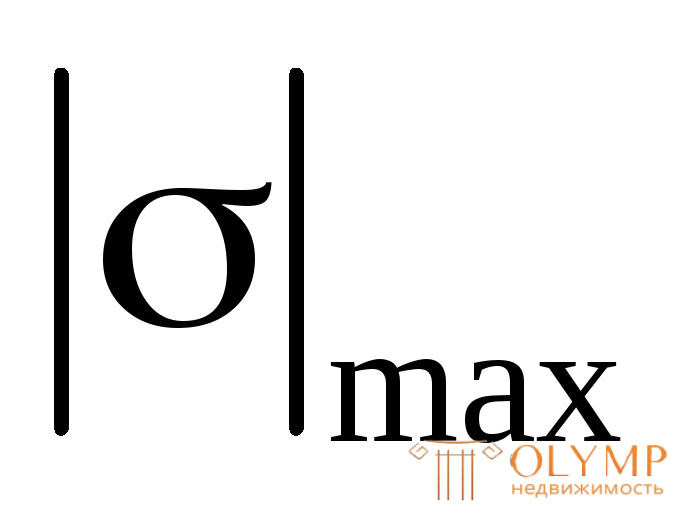 = R и из этого условия определяем требуемое значение осевого момента сопротивления:
= R и из этого условия определяем требуемое значение осевого момента сопротивления:
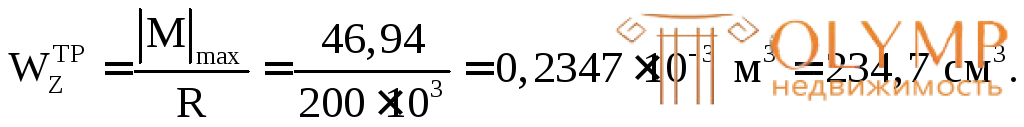
Определяем положение главной центральной оси Zи величину главного центрального момента инерции заданного сечения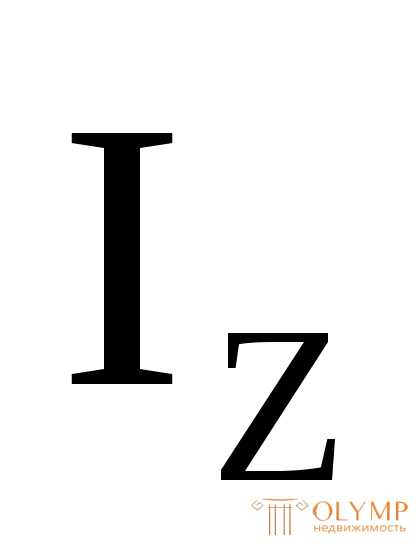 (см. главу 5). Геометрические характеристики плоских сечений:
(см. главу 5). Геометрические характеристики плоских сечений:
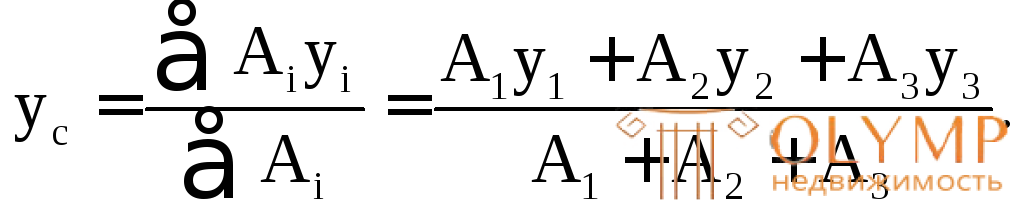
Здесь ус – расстояние от произвольно взятой оси Z' до центральной оси Z для всей фигуры; Аi – площади отдельных фигур:
А1= 10δ2= 202; А2= 22= 222; А3= 52= 102;
уi– ординаты центров тяжестей отдельных фигур относительно произвольно взятой оси Z'. Пусть произвольная ось Z' совпадает с осью Z3 (см. рис. 7.12г).
у1=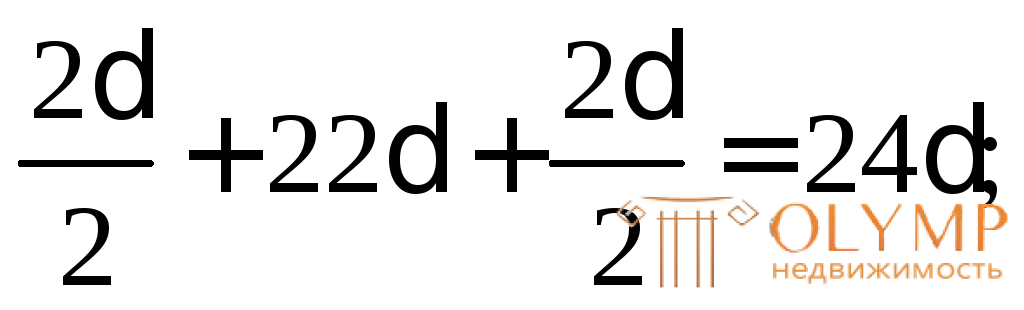 у2=
у2=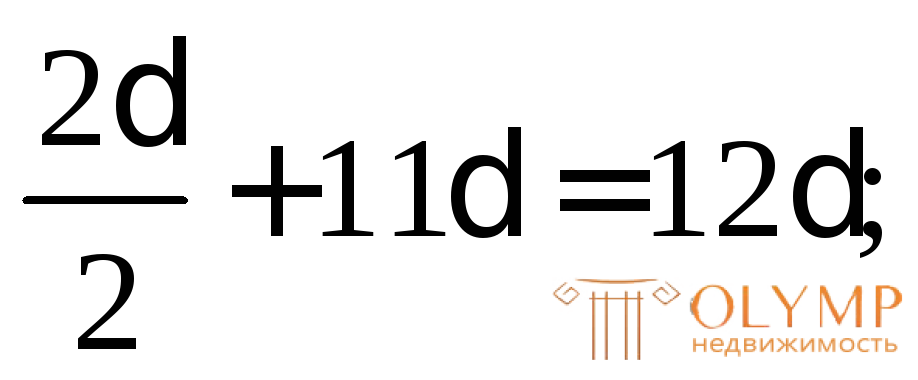
у3= 0, так как оси Z3 иZ' совпадают.
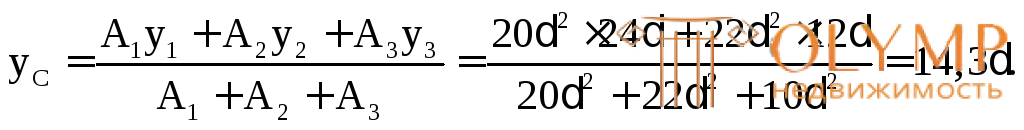
Отложим найденное расстояние yС от оси Z' и проведем общую центральную ось Z.
Осевой момент инерции всей фигуры относительно оси Z вычислим по формуле:
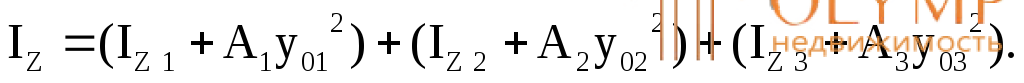
Здесь IZi – собственные моменты инерции простых фигур относительно их собственных центральных осей.
Так как все фигуры прямоугольники, то:
IZ1=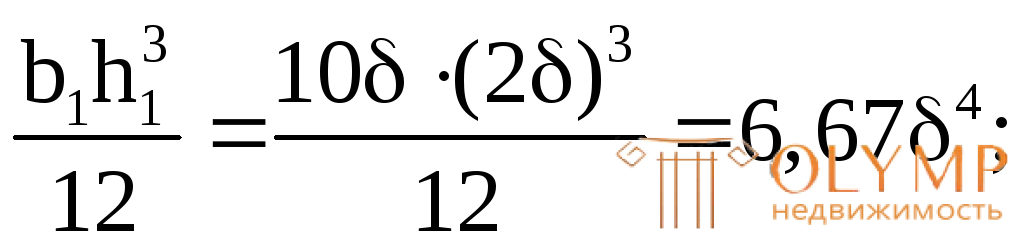
IZ2=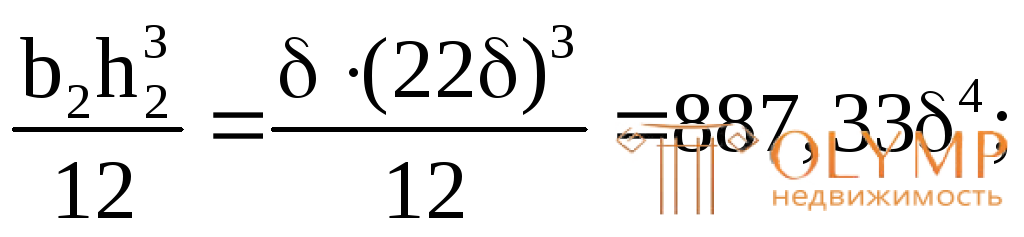
IZ3=
у0i – расстояния от общей центральной осиZдо центральных осей простых фигур Zi:
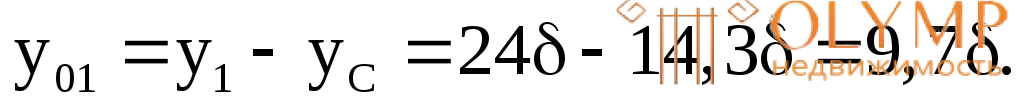
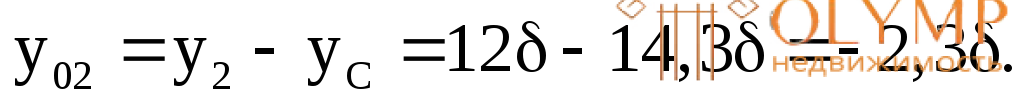
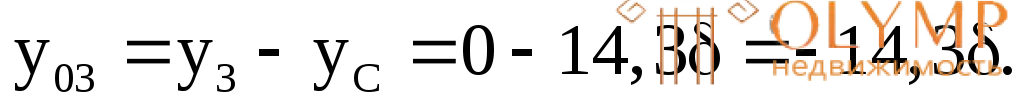

Б. Определим осевой момент сопротивления сечения.
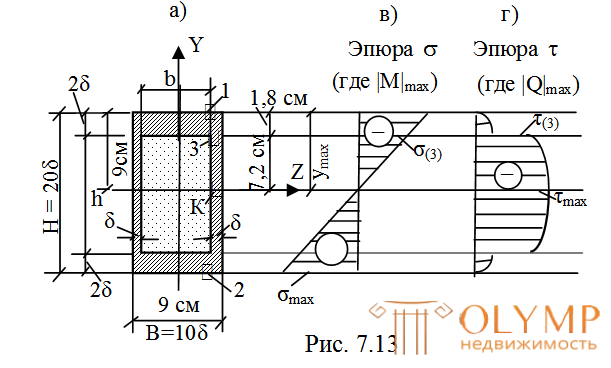
Расстояния от центральной (нейтральной) оси Zдо наиболее удаленных (крайних) точек сечения А и В (рис. 7.13а):
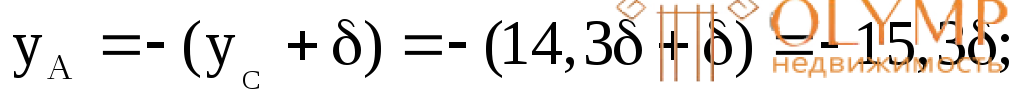
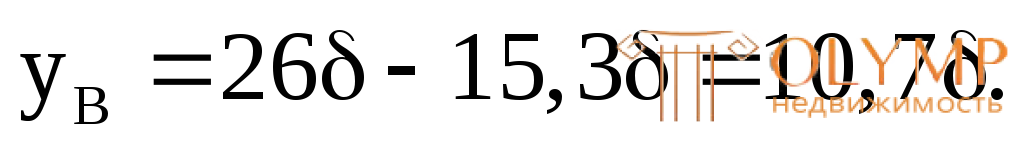
Отсюда: 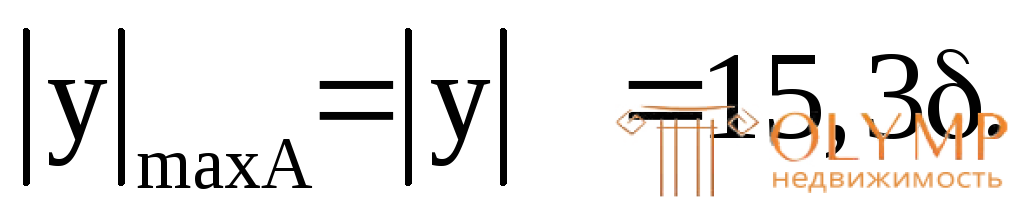
Осевой момент сопротивления определим по формуле:
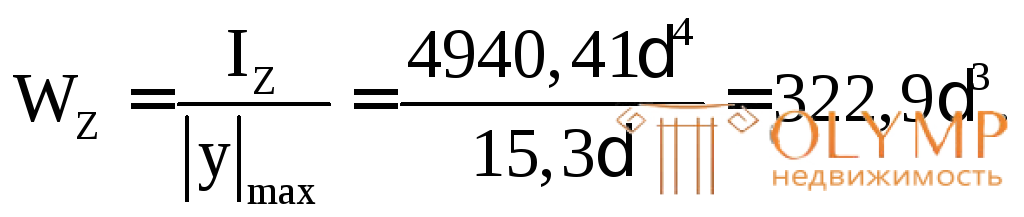
В. Приравняем найденное ранее значение требуемого осевого момента сопротивления к выражению для определения фактической величины осевого момента сопротивленияи найдем параметр сечения :
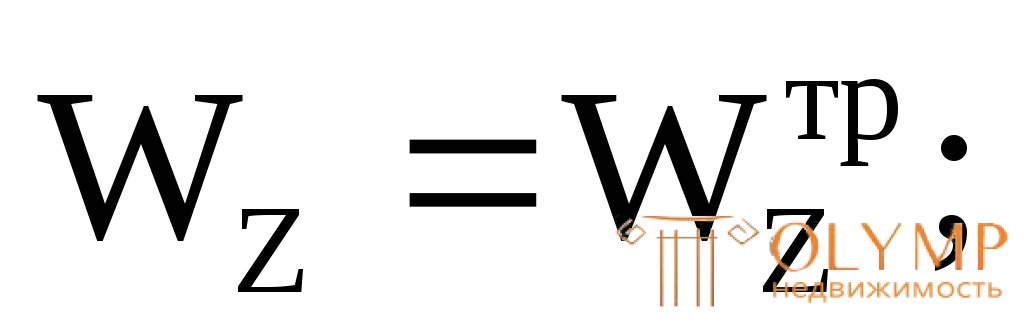
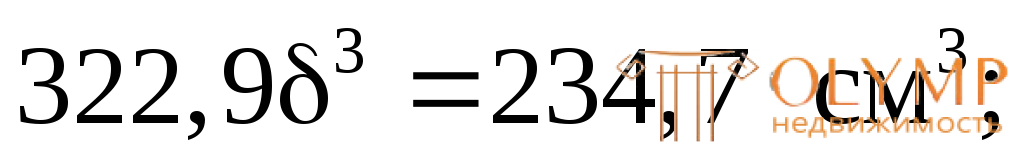

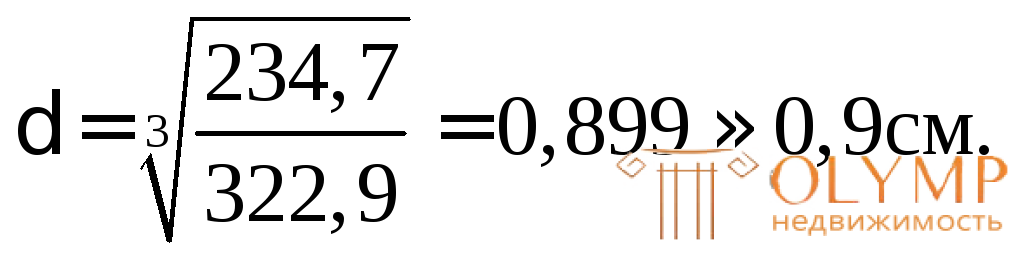
2. Расчет балки по 2-му варианту сечения (см. рис. 7.12д и 7.13а) R = 200М Па, RS= 100 МПа.
А. Определение осевого момента сопротивления сечения
Так как сечение имеет две оси симметрии, его центр тяжести находится на их пересечении.
Определим главный центральный момент инерции сечения относительно оси Z как разность моментов инерции двух прямоугольников, центры тяжести которых совпадают.
IZ=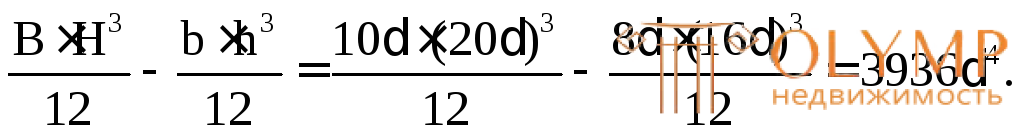
WZ=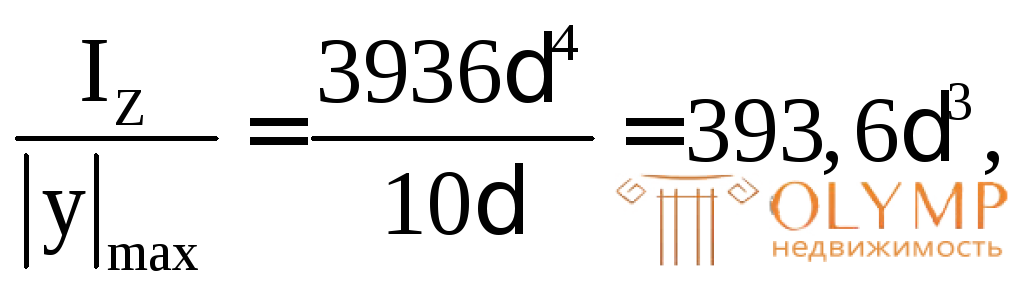 здесь
здесь 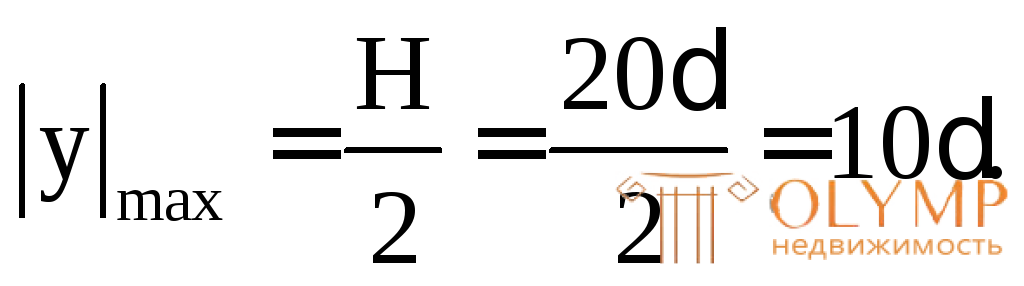
Б. Определение требуемого момента сопротивления сечения
Из условия прочности по нормальным напряжениям
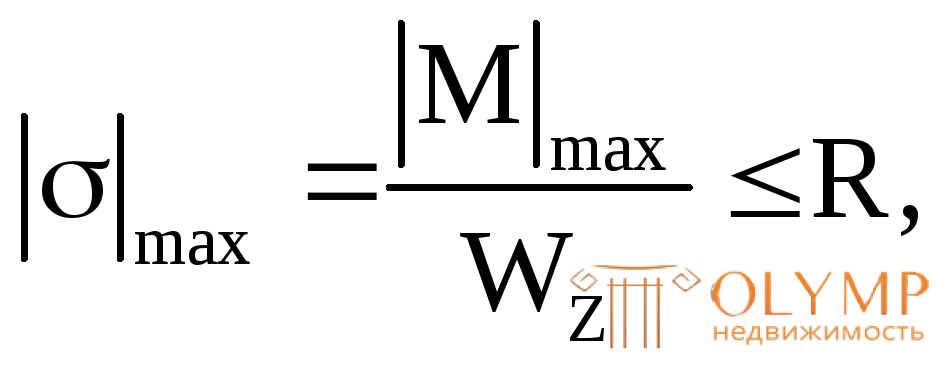 при
при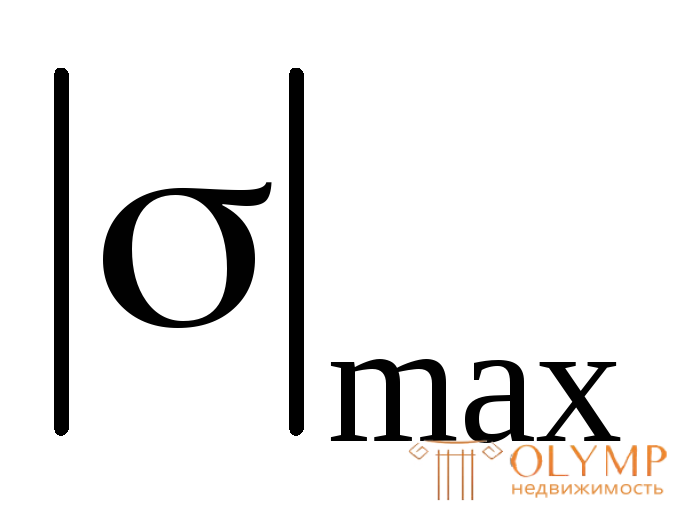 = R получаем
= R получаем
W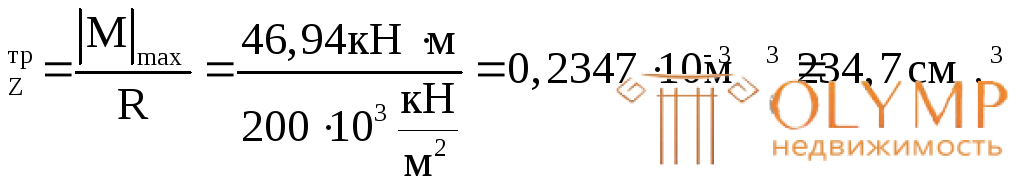
В. Из условия WZ = W определим размер
определим размер 
393,6  = 234,7 см3;
= 234,7 см3;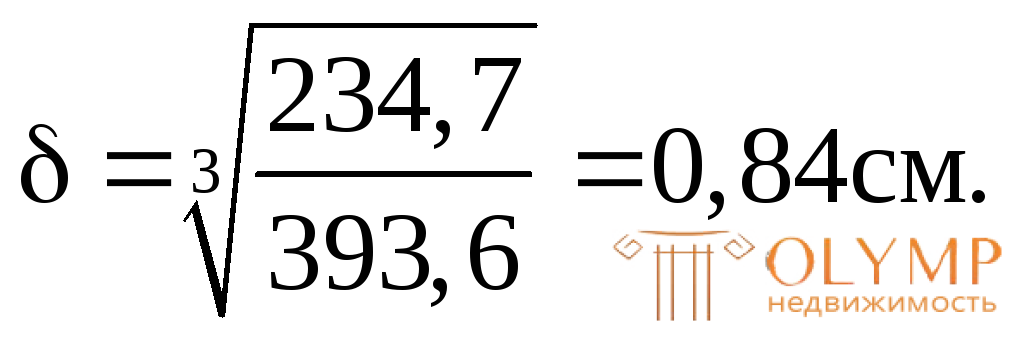
Полученное значение  округляем по ГОСТ 103-76 для стальной полосы и принимаем
округляем по ГОСТ 103-76 для стальной полосы и принимаем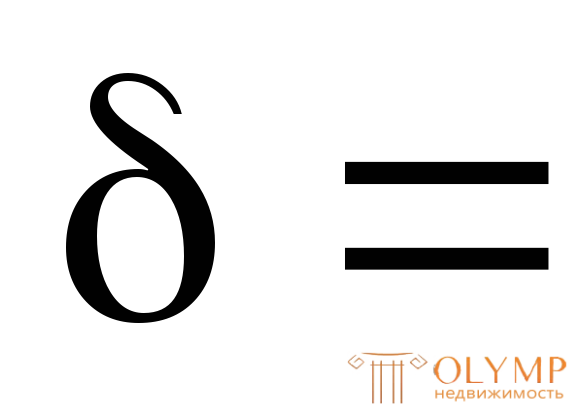 9 мм = 0,9 см.
9 мм = 0,9 см.
Г. Проверим прочность подобранного сечения по нормальным и касательным напряжениям
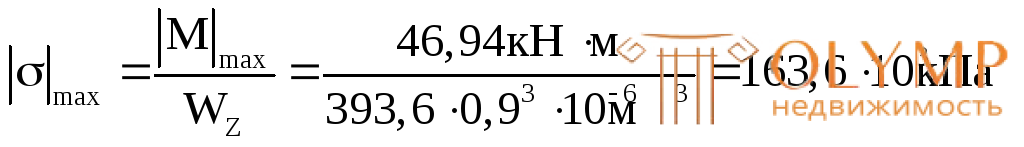 <R.
<R.
Имеется недонапряжение из-за округления размера сечения в большую сторону. Оценим его в процентах:
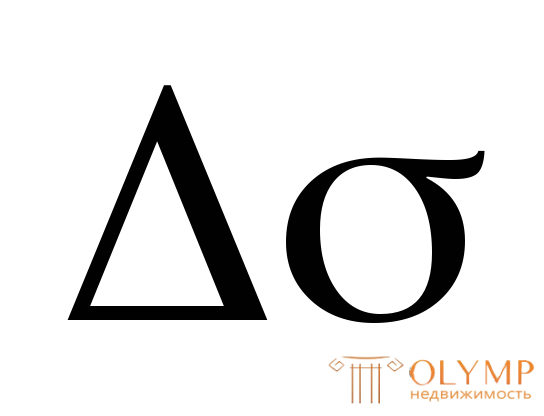 (%) =
(%) =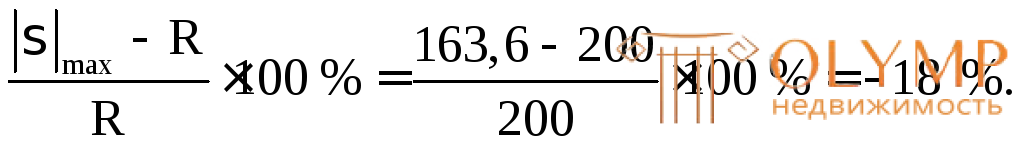
Из рис. 7.13г видно, что наибольшие касательные напряжения будут в точке К, лежащей на центральной оси.
Условие прочности:
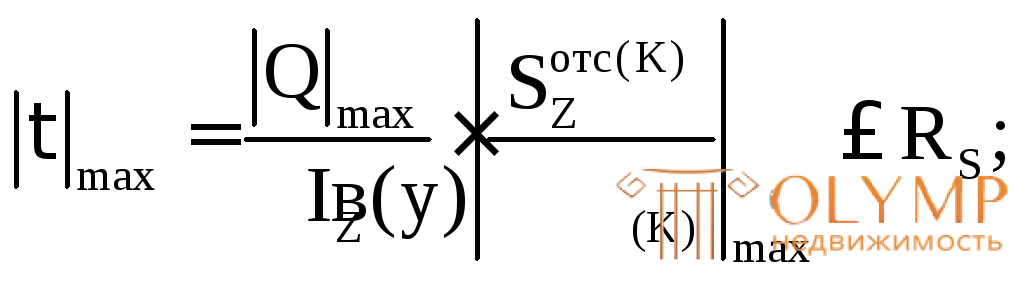
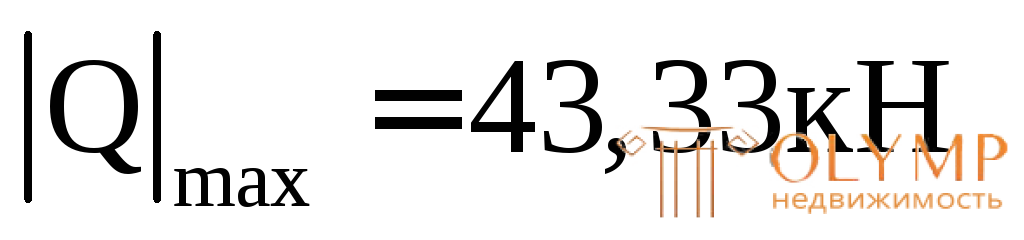 (из эпюрыQ, см. рис. 7.12б);
(из эпюрыQ, см. рис. 7.12б);
IZ= 3936 = 3936
= 3936 0,94= 2582 см4;
0,94= 2582 см4;
в(у)(к)= 2 = 2
= 2 0,9 = 1,8 см;
0,9 = 1,8 см;
S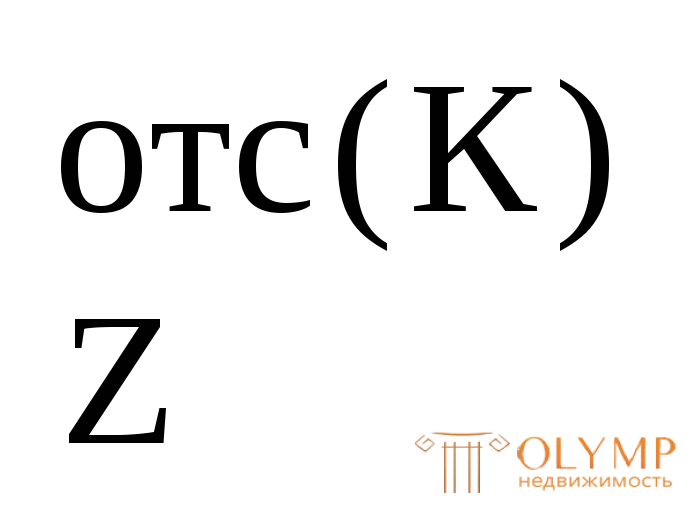 находим как разность статических моментов площадей, лежащих выше центральной оси Z, относительно этой же оси:
находим как разность статических моментов площадей, лежащих выше центральной оси Z, относительно этой же оси:
S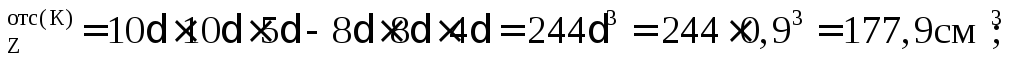
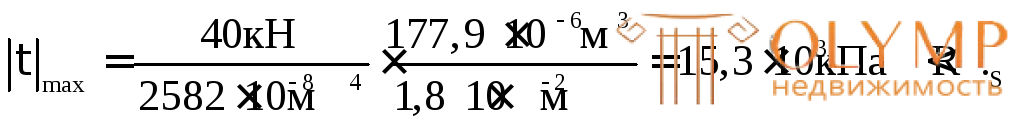
Условие прочности по касательным напряжениям выполняется с большим запасом.
ПРИМЕР 7.3
Для балки составного сечения (см. рис. 7.12г), рассчитанной в примере 7.2, требуется:
1. Выполнить полную проверку прочности балки при R = = 200 МПа, RS= 100 МПа.
2. Подобрать размер сечения по методу предельного равновесия (при коэффициенте запасаn= 1,2 и
по методу предельного равновесия (при коэффициенте запасаn= 1,2 и = 240 МПа) и сравнить его с величиной, полученной по методу расчетных сопротивлений в примере 7.2.
= 240 МПа) и сравнить его с величиной, полученной по методу расчетных сопротивлений в примере 7.2.
А. Проверка по нормальным напряжениям вточке А (рис. 7.14а), наиболее удаленной от нейтральной оси в 1-м опасном сечении, т.е. там,где действует наибольший по модулю изгибающий момент |M|max= 46,94 кНм при = 0,9 см:
= 0,9 см:
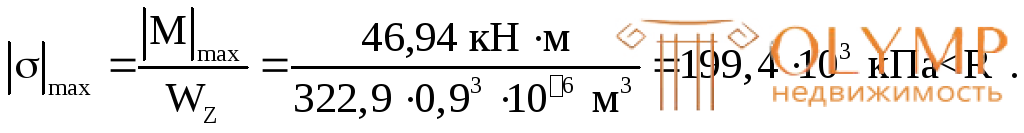
Имеет место небольшое недонапряжение ввиду округления  в большую сторону.
в большую сторону.
(%) = 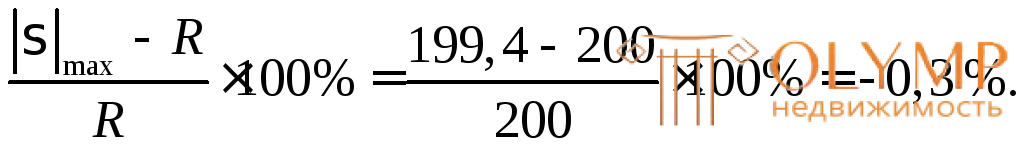
Б. Проверка прочности по касательным напряжениям в поперечном сечении во 2-м опасном сечении, т.е. там, где действует наибольшая по модулю поперечная сила |Q|max = 43,3 кН(см. эпюру Q, сечение 1–1, рис. 7.12).
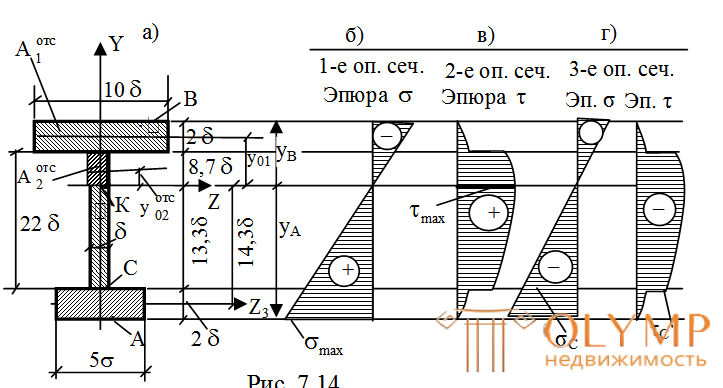
Для данного сечения наибольшие касательные напряжения будут действовать в точках, лежащих на центральной (нейтральной) оси (см. эпюру τ на рис. 7.14в):
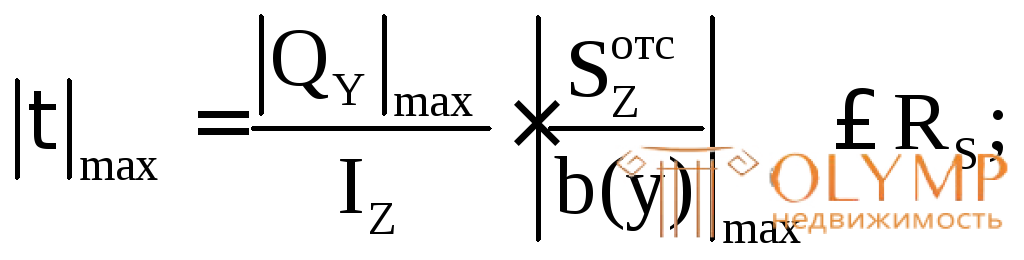
IZ= 4940,41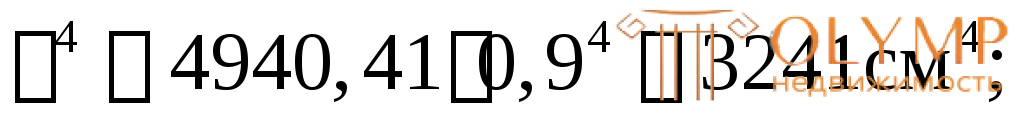 b(у)(К)=
b(у)(К)= = 0,9 см.
= 0,9 см.
Статически момент отсеченной части, находящейся выше центральной оси относительно этой же оси Z определим как сумму статических моментов двух прямоугольников:
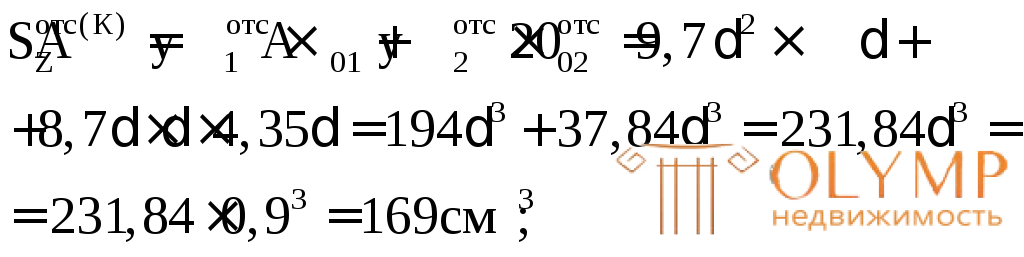
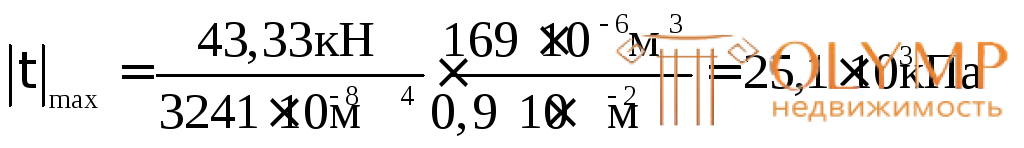 <RS.
<RS.
Условие прочности по касательным напряжениям в поперечном сечении выполняется с большим запасом.
В. Проверка прочности в 3-м опасном сечении, т.е. там, где одновременно действуют сравнительно большие изгибающий момент и поперечная сила, на совместное действие нормальных и касательных напряжений.
В данном примере таким сечением является сечение 5–5, где МIII= –40 кН м, QIII= –36,67 кН.
м, QIII= –36,67 кН.
Анализ эпюр нормальных и касательных напряжений (см. рис. 7.14б, в) показывает, что в тех точках поперечного сечения, где действуют наибольшие нормальные напряжения ||max(это наиболее удаленная от нейтральной оси Z точка А), имеет место одноосное напряженное состояние, так как там отсутствуют касательные напряжения и мы пренебрегаем давлением волокон друг на друга, т.е. σy= 0; σx= σ (рис. 7.15г). В этой точке прочность уже проверена.
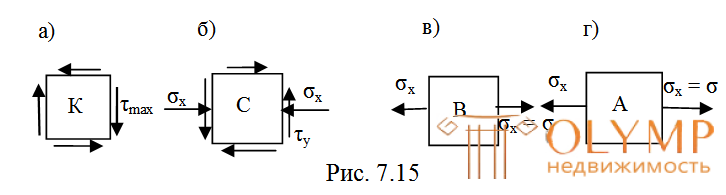
В точках поперечного сечения, лежащих на нейтральной оси Zдействуют только касательные напряжения, а нормальные напряжения равны нулю, т.е. там имеет место чистый сдвиг (точкаK на рис. 7.14а). Прочность в этой точке по касательным напряжениям тоже проверена.
Остается проверить прочность в сечении 5–5 (см. рис. 7.12а),где имеет место наиболее неблагоприятное сочетание значений изгибающего момента и поперечной силы (М = –40 кН м, Q = = –36,67 кН) на совместное действие нормальных и касательных напряжений в тех точках, где они одновременно принимают сравнительно большие значения. Такой точкой является точка С (см. рис. 7.13а). В такой точке имеет место плоское напряженное состояние.
м, Q = = –36,67 кН) на совместное действие нормальных и касательных напряжений в тех точках, где они одновременно принимают сравнительно большие значения. Такой точкой является точка С (см. рис. 7.13а). В такой точке имеет место плоское напряженное состояние.
Для проверки прочности в точке С используем 3-ю теорию прочности – теорию наибольших касательных напряжений.
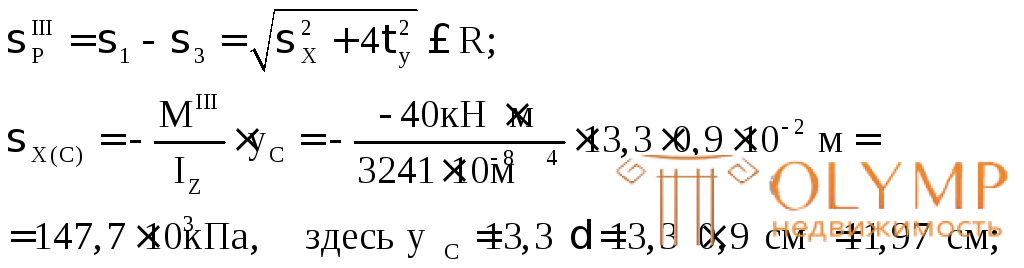
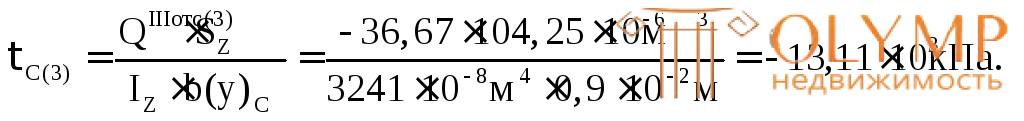
Здесь
S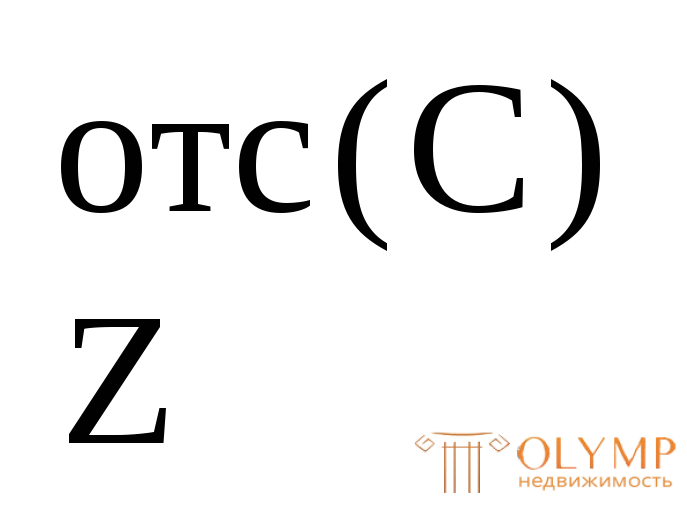 = 5
= 5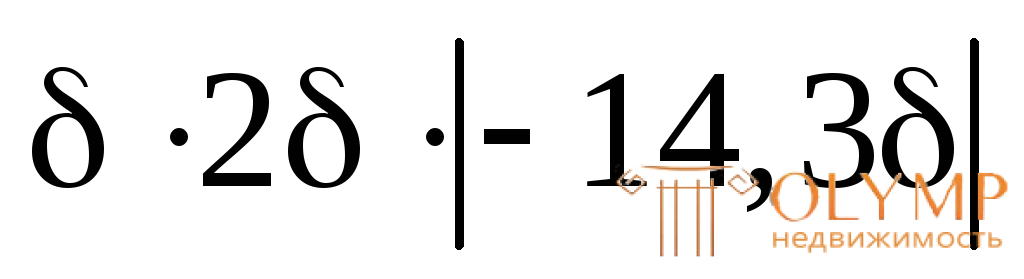 = 143
= 143 = 143
= 143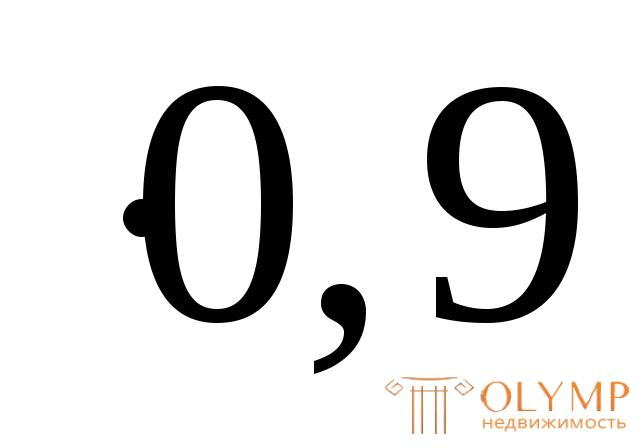 = 104,25 см3;
= 104,25 см3;
b(y)С =  = 0,9 см;
= 0,9 см;
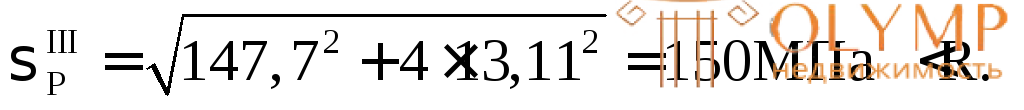
Из условия прочности по методу предельного равновесия (7.12) определим параметр заданного сечения  и сравним его с этим же параметром, полученным из расчета по методу расчетных сопротивлений.
и сравним его с этим же параметром, полученным из расчета по методу расчетных сопротивлений.
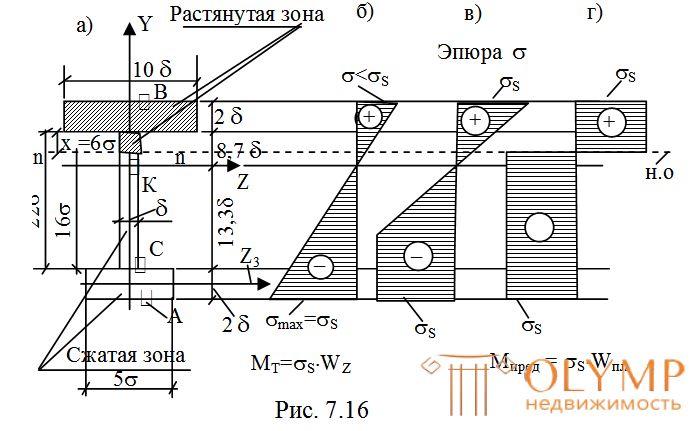
Как было показано ранее, в предельном состоянии нейтральная ось n–n делит сечение на две равновеликие части – растянутую и сжатую зоны. Из условия Ар= Асж=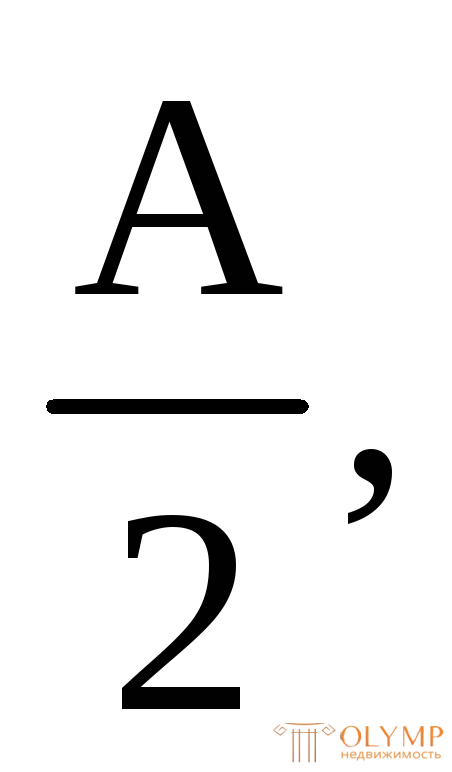 где А = = 20
где А = = 20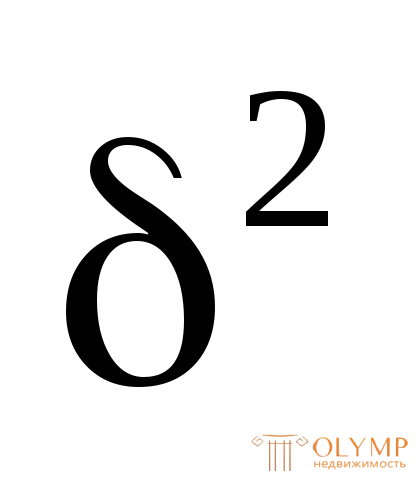 + 22
+ 22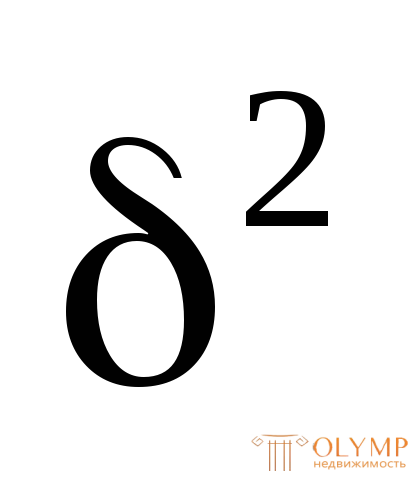 + 10
+ 10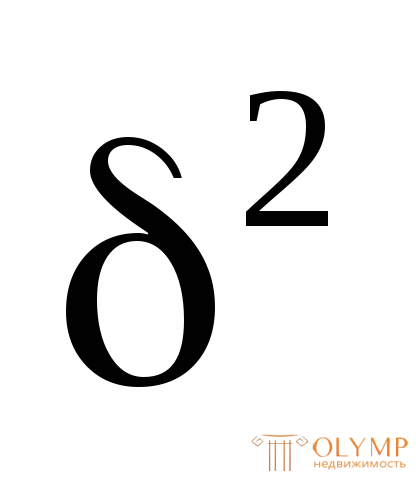 = 52
= 52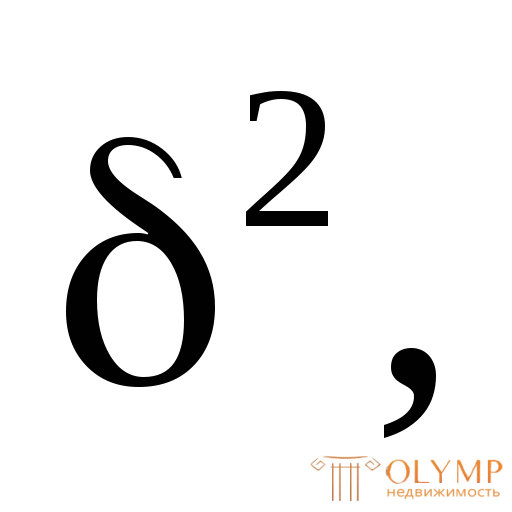 определим положение нейтральной осиn–nв предельном состоянии (рис. 7.16а) из выражения для определения площади растянутой зоны, состоящей из двух прямоугольников с площадями 102и х:
определим положение нейтральной осиn–nв предельном состоянии (рис. 7.16а) из выражения для определения площади растянутой зоны, состоящей из двух прямоугольников с площадями 102и х:
Ар= 20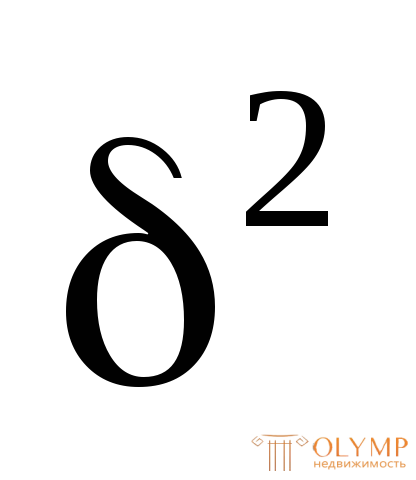 + х
+ х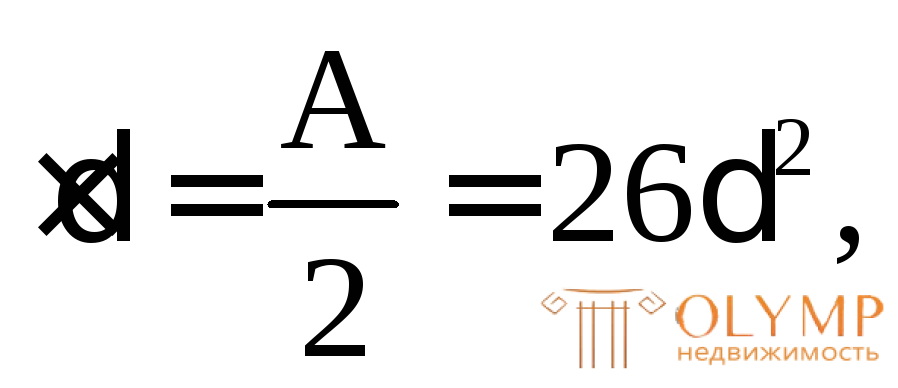 отсюда х = 6
отсюда х = 6 .
.
Определим статические моменты растянутой (верхней) и сжатой (нижней) зон относительно нейтральной оси n–n.
S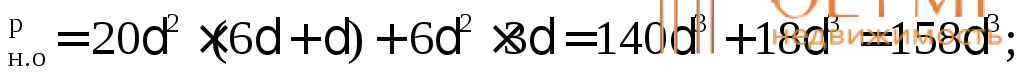
S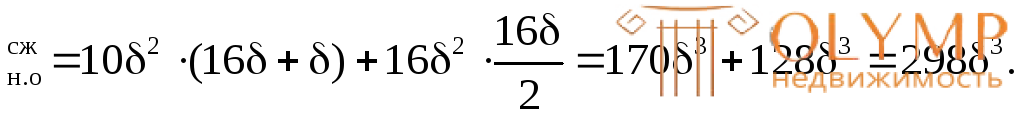
Определим пластический момент сопротивления сечения: Wпл= S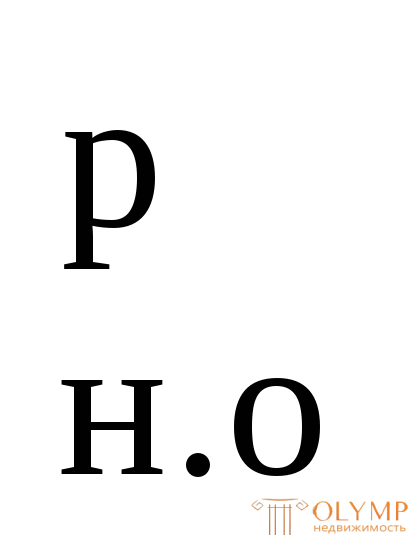 + S
+ S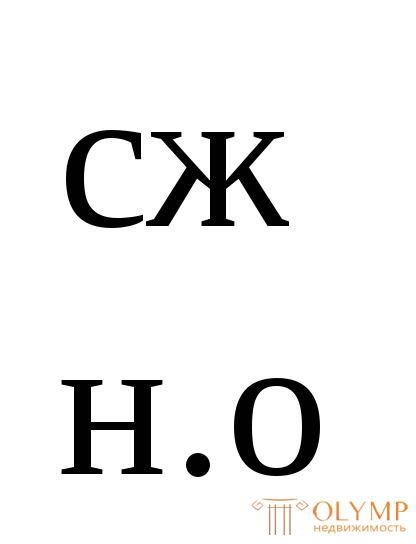 = 158
= 158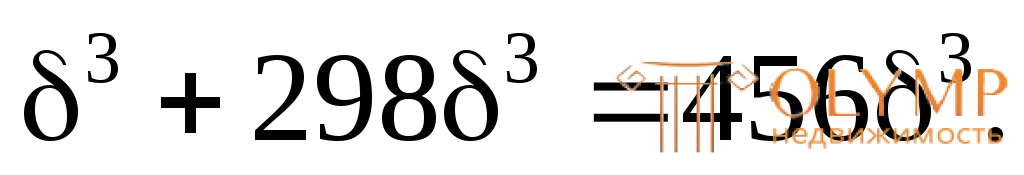
Из условия прочности по методу предельного равновесия определим неизвестный параметр сечения :
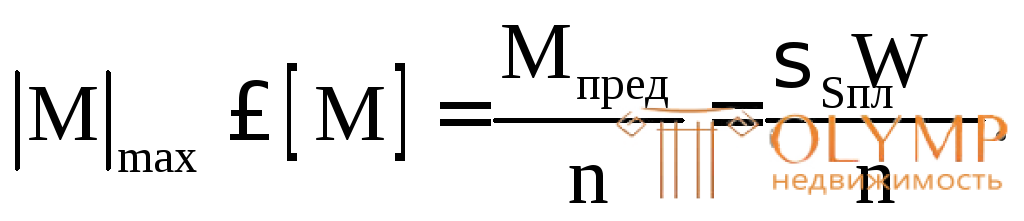
При S= 240 103кПа,n= 1,2 имеем:
103кПа,n= 1,2 имеем:
46,94 кН м =
м =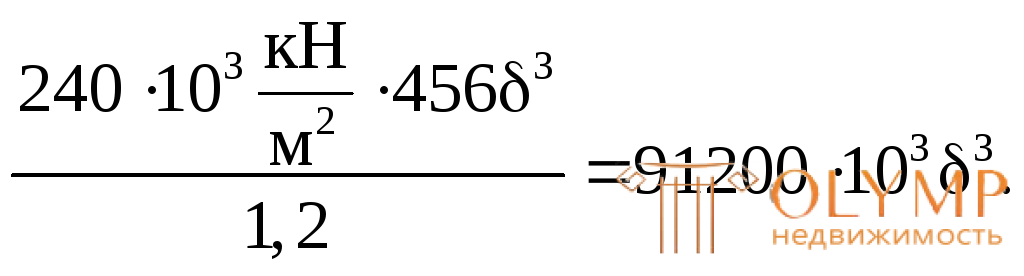
Отсюда 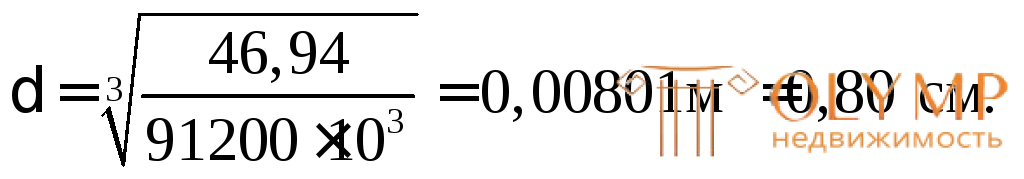
+ 
Сравним расход материала по площади сечения при размере сечения δ2= 0,8 см с площадью сечения при размере1= 0,9 см, полученном по методу расчетных сопротивлений):
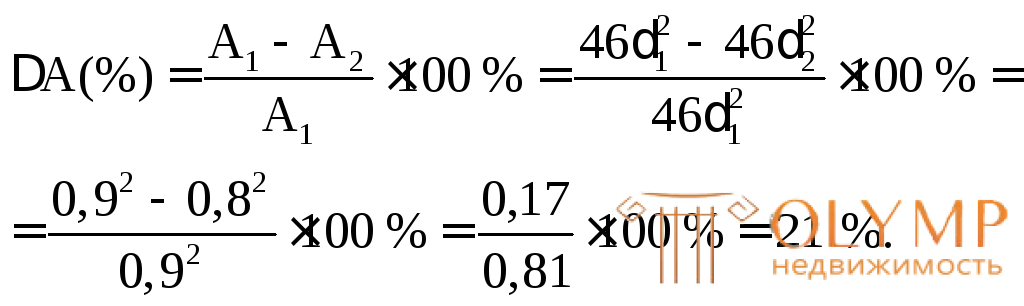
Видно, что по методу предельного равновесия балка получается на 21 % легче по весу, т.е. по расходу материала.
Какой вид деформации называется прямым изгибом? Какая разница между чистым и поперечным изгибом?
Какие внутренние силовые факторы возникают в поперечных сечениях бруса при прямом поперечном изгибе? Как они определяются?
В чем заключается суть метода сечений при определении внутренних усилий?
Дайте определение понятия "грузовой участок". Какие внешние признаки определяют границы грузовых участков?
Каков порядок построения эпюр Qи М в балках?
Какие дифференциальные зависимости существуют между функциями М, Qиq?
Какие особенности имеют эпюры М и Q на границах и по длине грузовых участков в зависимости от приложенных внешних сил?
По какой формуле определяются нормальные напряжения при прямом изгибе в произвольной точке поперечного сечения? Покажите их эпюры на рисунке.
Как определяются касательные напряжения при прямом поперечном изгибе в произвольной точке поперечного сечения? Изобразите их эпюры для некоторых типов сечений.
Напишите условия прочности при прямом изгибе по нормальным напряжениям для балок из пластичного и хрупкого материалов.
Какие три типа задач можно решать, используя условия прочности при изгибе?
Каков порядок подбора сечения балки из условия прочности по нормальным напряжениям?
Запишите условие прочности балки по касательным напряжениям.
Как выполняется полная проверка прочности балки?
В каких точках поперечного сечения балки имеет место одноосное, плоское напряженные состояния и чистый сдвиг?
В чем заключается суть расчета балки по методу предельной несущей способности?
Как определяется положение нейтральной оси при расчете балки по методу предельной несущей способности?
Что называется пластическим моментом сопротивления сечения?
Как определяется значение предельного изгибающего момента?
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Что бы оставить комментарий войдите
Комментарии (0)