Расчет по методу предельной несущей способности кратко

В методе расчетных сопротивлений, рассмотренном ранее, условие прочности ограничивает достижение хотя бы в одной точке поперечного сечения напряжения, равного расчетному сопротивлению для данного материала, т.е. 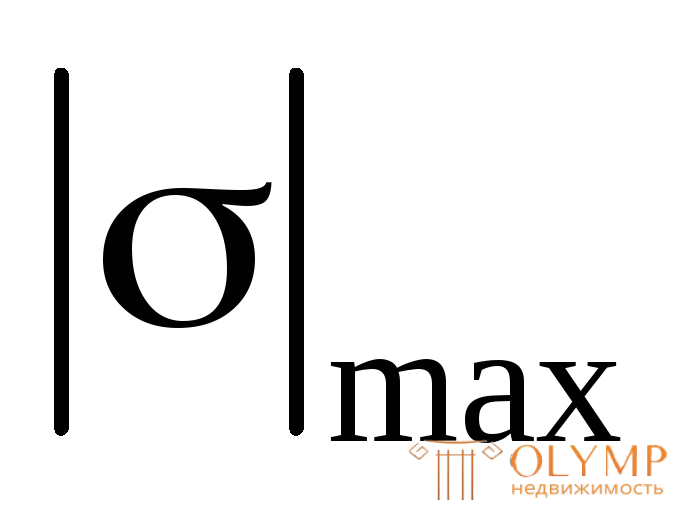R.

В методе предельной несущей способности условие прочности относится не к напряжению, а к допускаемому изгибающему моменту, который определяется как отношение предельного изгибающего момента к коэффициенту запаса n.

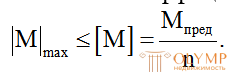(7.12)

При одинаковом значении коэффициента запаса по напряжениям и по нагрузкам (т.е. 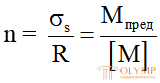) метод предельной несущей способности дает некоторую экономию материала.

Рассмотрим метод предельного равновесия при изгибе балок из упруго-пластического материала (например, сталь).

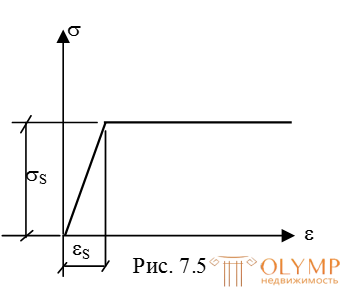Для упрощения задачи примем в качестве расчетной диаграмму Прандтля (рис. 7.5). При < _Sматериал работает линейно-упруго, поэтому для вычисления нормальных напряжений в поперечном сечении балки справедлива формула: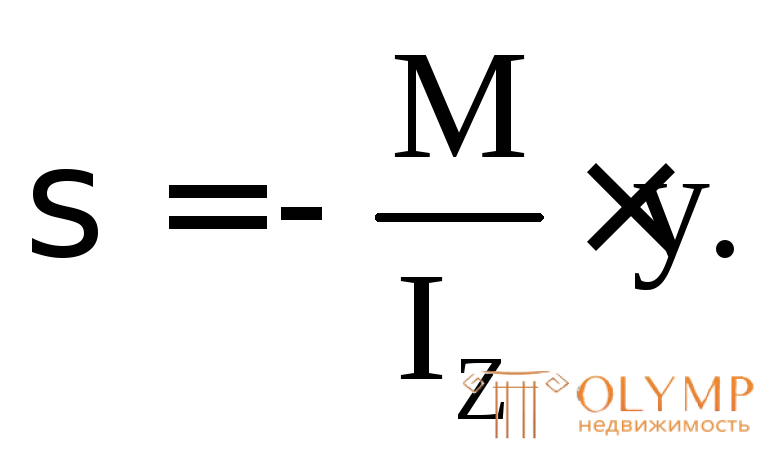

При достижении максимального значения нормального напряжения в наиболее удаленной от центральной (нейтральной) оси сечения точке предела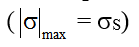 текучести продольные волокна в этой точке неограниченно деформируются при постоянном напряжении = _S.

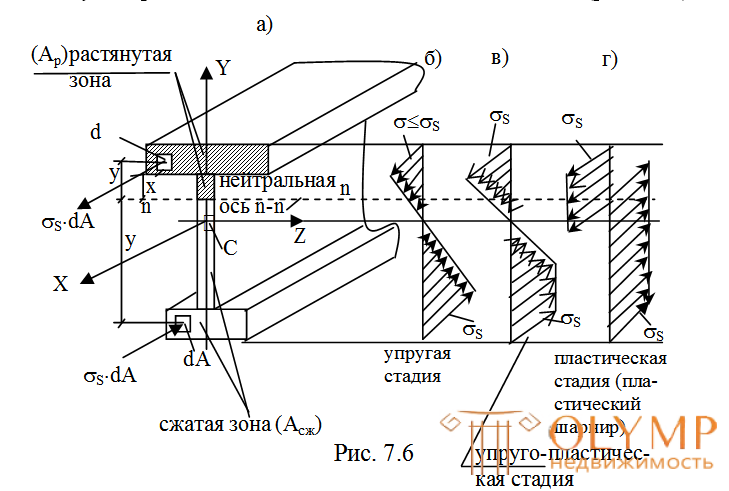
При таком предположении рассмотрим стадии, проходящие балкой при увеличении изгибающего момента в данном сечении вплоть до исчерпания несущей способности (рис. 7.6).

При постепенном возрастании максимального изгибающего момента линейно-упругая стадия работы балки заканчивается при достижении текучести в самой напряженной крайней точке (рис. 7.6б). Соответствующий данному состоянию изгибающий момент определится из условия

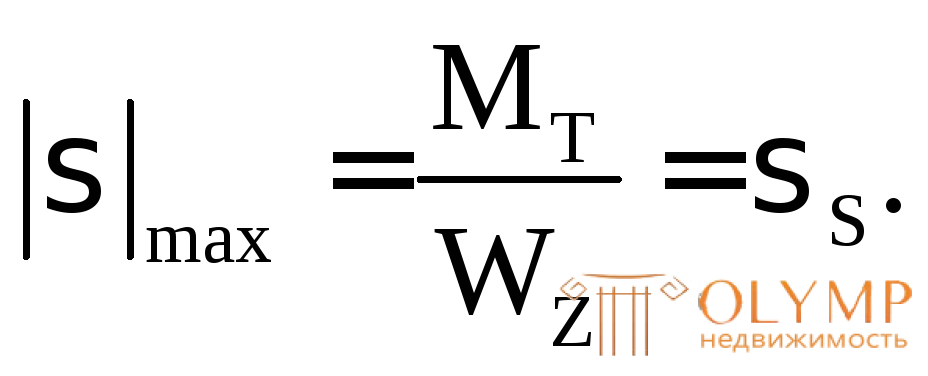
Отсюда М_Т=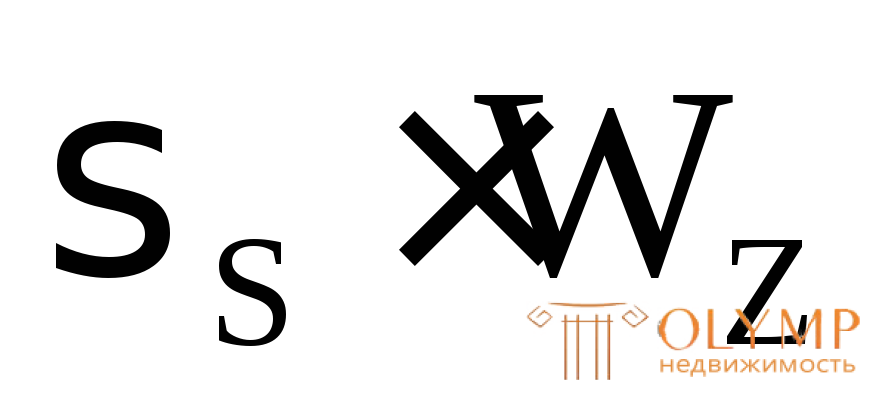. (7.13)

При дальнейшем увеличении внешней силы, а значит и максимального изгибающего момента, наступает упруго-пластическая стадия работы балки. Зона текучести при этом будет расширяться от крайних точек, а эпюра при М_ТММ_предбудет иметь вид (рис. 7.6в). В пределе эпюрапревратится в ступенчатую эпюру с ординатами = _S. В данный момент это сечение будет работать в чисто пластической стадии (рис. 7.6г).

Если центральная ось Z является осью симметрии сечения, то обе крайние точки достигают текучести одновременно.

Состояние сечения, когда во всех точках развиваются пластические деформации, называют пластическим шарниром.

При этом балка, если она была статически определимой, как бы превращается в механизм, продолжающий увеличивать прогибы при постоянной внешней нагрузке, равной предельной. Такое состояние называют пластическим механизмом. В поперечном сечении, где образовался пластический шарнир, внутренний момент обозначим М_преди назовем егопластическим предельным моментом.

Таким образом, наиболее напряженное сечение балки проходит три стадии работы:

– линейно упругую ();

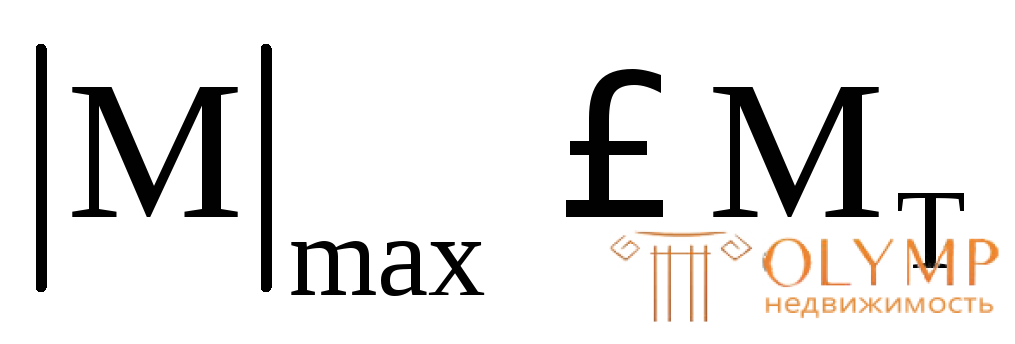– упруго пластическую (М_Т < 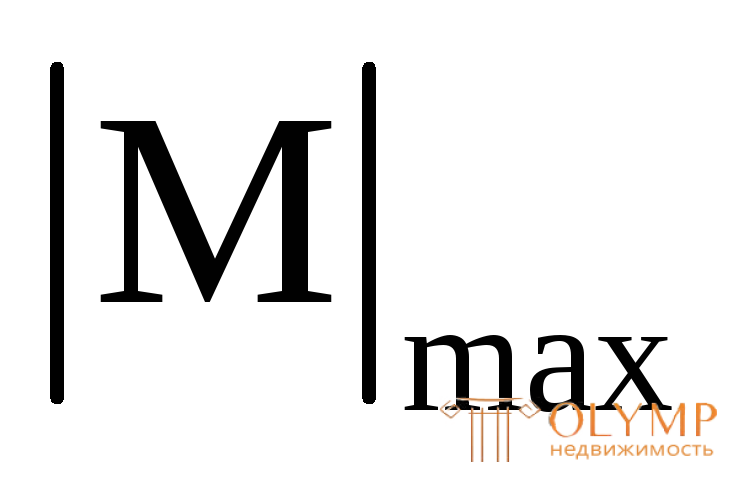< М_пред.);

– чисто пластическую (пластический шарнир) (|M|_max = M_пред).

Получим формулу для определения М_предна примере сечения с одной осью симметрии (рис. 7.6).

В упругой стадии эпюра линейна и нулевая (нейтральная) линия совпадает с центральной осью Z.

В общем случае при образовании пластического шарнира нейтральная ось (н.о) n–nсмещается от центра тяжести сечения (точки С). В этот момент все сечение делится на две части: часть, растягиваемую постоянным напряжением_Sс площадью А_р и соответствующей силойN_P= А_P  _S и часть сжимаемую постоянным напряжением_Sс площадью А_сжс действующей силой N_cж= –А_сж_S. Так как суммарная продольная сила в сечении при поперечном изгибе равна нулю, то из условия:

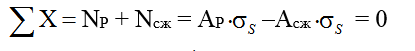
получим А_р= А_cж=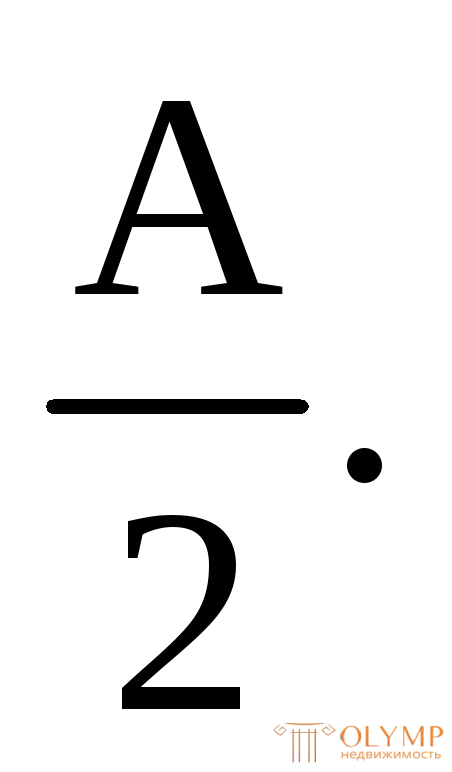

Таким образом, при образовании пластического шарнира нейтральная ось делит площадь поперечного сечения на две равновеликие части.Эта ось на рис. 7.4 показана пунктиром.

Внутренний момент М_преднайдем как момент всех элементарных сил (_S dA) относительно нейтральной оси n–n, (рис. 7.6а).

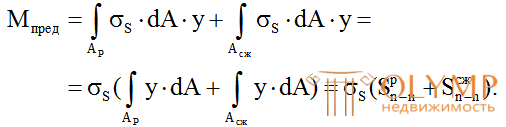(7.14)

Здесь – 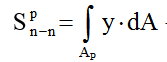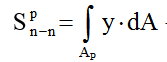статический момент растянутой зоны относительно нейтральной оси в предельном состоянииn–n;S 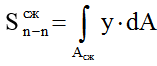– то же для сжатой зоны.

Обозначим S+ S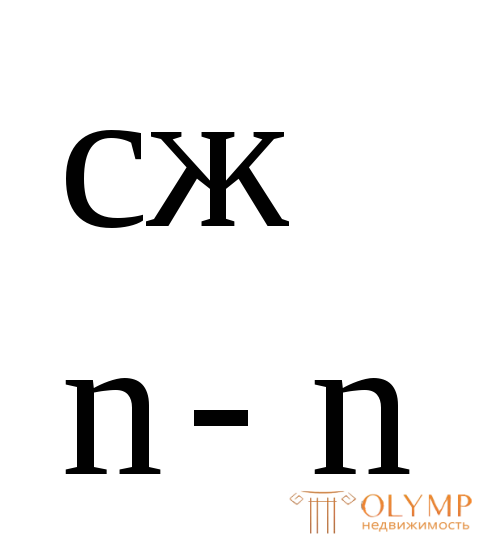= W_пл, (7.15)

где W_пл–пластический момент сопротивления сеченияв отличие от 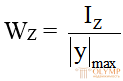осевого момента сопротивления в упругой стадии.

Формулу (7.14) можно записать в виде, аналогичном соответствующей формуле в упругой стадии:

М_пред=(7.16)