3.14. Железобетонные элементы рассчитывают по прочности на действие изгибающих моментов, поперечных сил, продольных сил, крутящих моментом и на местное действие нагрузки (местное сжатие, продавливание, отрыв).
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ НА ДЕЙСТВИЕ ИЗГИБАЮЩИХ МОМЕНТОВ
Общие положения
3.15. Расчет по прочности железобетонных элементов на действие изгибающих моментов следует производить для сечений, нормальных к их продольной оси.
Расчет нормальных сечений изгибаемых элементов следует производить на основе нелинейной деформационной модели согласно пп.3.72 - 3.76, принимая N = 0.
Расчет прямоугольного, таврового и двутаврового сечений с арматурой, расположенной у перпендикулярных плоскости изгиба граней элемента, при действии момента в плоскости симметрии сечения допускается производить по предельным усилиям согласно пп.3.17-3.27.
Расчет элементов с такими сечениями на действие косого изгиба в некоторых случаях также допускается производить по предельным усилиям согласно пп.3.28 и 3.29.
3.16. Для железобетонных элементов, у которых предельный по прочности изгибающий момент оказывается меньше момента образования трещин (пп.4.5-4.8), площадь сечения продольной растянутой арматуры должна быть увеличена по сравнению с требуемой из расчета по прочности не менее чем на 15% или должна удовлетворять расчету по прочности на действие момента образования трещин.
3.17. Расчет по прочности нормальных сечений следует производить в зависимости от соотношения между значением относительной высоты сжатой зоны бетона 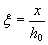 , определяемым из соответствующих условий равновесия, и значением граничной относительной высоты сжатой зоны ξR при котором предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rs.
, определяемым из соответствующих условий равновесия, и значением граничной относительной высоты сжатой зоны ξR при котором предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rs.
Значение ξR определяют по формуле
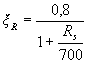 (3.15)
(3.15)
где Rs - в МПа или по табл. 3.2.
Таблица 3.2
|
Класс арматуры |
А240 |
А300 |
А400 |
А500 |
В500 |
|
Значение ξR |
0,612 |
0,577 |
0,531 |
0,493 |
0,502 |
|
Значение aR |
0,425 |
0,411 |
0,390 |
0,372 |
0,376 |
Прямоугольные сечения
3.18. Расчет прямоугольных сечений (черт.3.3) производится следующим образом в зависимости от высоты сжатой зоны
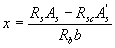 (3.16)
(3.16)
а) при 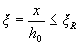 - из условия
- из условия
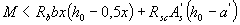 (3.17)
(3.17)
б) при 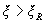 - из условия
- из условия
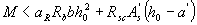 (3.18)
(3.18)
где 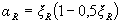 или см. табл. 3.2.
или см. табл. 3.2.
Правую часть условия (3.18) при необходимости можно несколько увеличить путем замены значения aR на (0,7aR + 0,3 am), где am = ξ(1 - 0,5 ξ), и принимая здесь ξ не более 1.
Если х ≤ 0, прочность проверяют из условия
M ≤ RsAs (h0-a') (3.19)
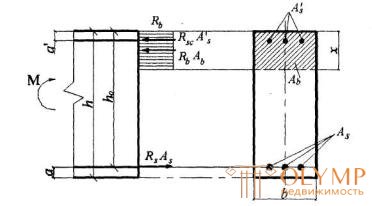
Черт.3.3. Схема усилий и эпюра напряжений в поперечном прямоугольном сечении изгибаемого железобетонного элемента
Если вычисленная без учета сжатой арматуры (As= 0,0) высота сжатой зоны х меньше 2а', проверяется условие (3.19), где вместо а' подставляется х/2.
3.19. Изгибаемые элементы рекомендуется проектировать так, чтобы обеспечить выполнение условия 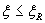 . Невыполнение этого условия можно допустить лишь в случаях, когда площадь сечения растянутой арматуры определена из расчета по предельным состояниям второй группы или принята по конструктивным соображениям.
. Невыполнение этого условия можно допустить лишь в случаях, когда площадь сечения растянутой арматуры определена из расчета по предельным состояниям второй группы или принята по конструктивным соображениям.
3.20. Проверку прочности прямоугольных сечений с одиночной арматурой производят:
при х < ξRho из условия
M ≤ RsAs (h0-0, 5x) (3.20)
где х - высота сжатой зоны, равная 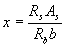 ; ξR - см. п.3.17;
; ξR - см. п.3.17;
при х ≥ ξRho из условия
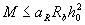 (3.21)
(3.21)
где aR - см. табл. 3.2;
при этом несущую способность можно несколько увеличить, используя рекомендацию п.3.18, б.
3.21. Подбор продольной арматуры производят следующим образом.
Вычисляют значение
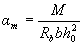 . (3.22)
. (3.22)
Если aт < ar (см. табл. 3.2), сжатая арматура по расчету не требуется.
При отсутствии сжатой арматуры площадь сечения растянутой арматуры определяется по формуле
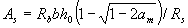 , (3.23)
, (3.23)
Если aт > ar , требуется увеличить сечение или повысить класс бетона, или установить сжатую арматуру согласно п.3.22.
3.22. Площади сечения растянутой As и сжатой A's арматуры, соответствующие минимуму их суммы, если по расчету требуется сжатая арматура (см. п.3.21), определяют по формулам:
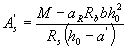 (3.24)
(3.24)
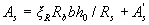 (3.25)
(3.25)
где ξR и ar см. табл. 3.2
Если значение принятой площади сечения сжатой арматуры As значительно превышает значение, вычисленное по формуле (3.24), площадь сечения растянутой арматуры можно несколько уменьшить по сравнению с вычисленной по формуле (3.25), используя формулу
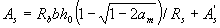 (3.26)
(3.26)
где 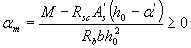
При этом должно выполняться условие aт < ar (см. табл. 3.2).
Тавровые и двутавровые сечения
3.23. Расчет сечений, имеющих полку в сжатой зоне (тавровых, двутавровых и т.п.), производят в зависимости от положения границы сжатой зоны:
а) если граница проходит в полке (черт. 3.4,а), т.е. соблюдается условие
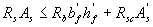 (3.27)
(3.27)
расчет производят по пп.3.18 и 3.20 как для прямоугольного сечения шириной 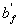 ;
;
б) если граница проходит в ребре (черт. 3.4,б), т.е. условие (3.27) не соблюдается, расчет производят из условия:
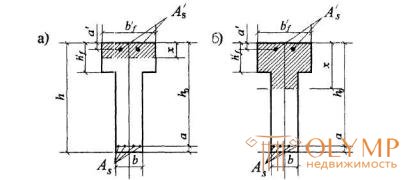
Черт.3.4. Положение границы сжатой зоны в тавровом сечении изгибаемого железобетонного элемента
а-в палке; б - в ребре
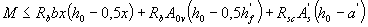 , (3.28)
, (3.28)
где А0v - площадь сечения свесов полки, равная (b'f -b)h'f, при этом высоту сжатой зоны определяют по формуле
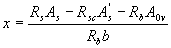 (3 29)
(3 29)
и принимают не более ξRho (см. табл. 3.2).
Если х> ξRho условие (3.28) можно записать в виде
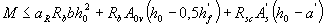 , (3.30)
, (3.30)
где aR - см. табл. 3.2.
Примечания: 1. При переменной высоте свесов полки допускается принимать значение h'f равным средней высоте свесов.
2. Ширина сжатой полки b'f, вводимая в расчет, не должна превышать величин, указанных в п. 3.26.
3.24. Требуемую площадь сечения сжатой арматуры определяют по формуле
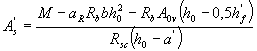 (3.31)
(3.31)
где aR - см. табл. 3.2; А0v = (b'f -b)h'f
При этом должно выполняться условие h'f ≤ ξRho В случае, если h'f > ξRho, площадь сечения сжатой арматуры определяют как для прямоугольного сечения шириной b = b'f по формуле (3.24).
3.25. Требуемую площадь сечения растянутой арматуры определяют следующим образом:
а) если граница сжатой зоны проходит в полке, т.е. соблюдается условие:
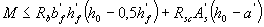 (3.32)
(3.32)
площадь сечения растянутой арматуры определяют как для прямоугольного сечения шириной b'f согласно п.3.21 и п.3.22;
б) если граница сжатой зоны проходит в ребре, т.е. условие (3.32) не соблюдается, площадь сечения растянутой арматуры определяют по формуле
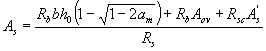 (3.33)
(3.33)
где 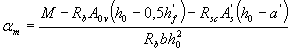 . (3.34)
. (3.34)
При этом должно выполняться условие aт ≤ ar (см. табл. 3.2).
3.26. Значение b'f вводимое в расчет, принимают из условия, что ширина свеса полки в каждую сторону от ребра должна быть не более 1/6 пролета элемента и не более:
а) при наличии поперечных ребер или при h'f ≥ 0,1h - 1/2 расстояния в свету между продольными ребрами;
б) при отсутствии поперечных ребер (или при расстояниях между ними, больших, чем расстояния между продольными ребрами) и при h'f < 0,1h - 6h'f ;
в) при консольных свесах полки
при h'f ≥ 0,1h - 6h'f ,
при 0,05h ≤ h'f < 0,1h - 3h'f;
при h'f < 0,05h - свесы не учитывают.
Примеры расчета
Прямоугольные сечения
Пример 2. Дано: сечение размером b = 300 мм, h = 600 мм; а = 40 мм; изгибающий момент с учетом кратковременных нагрузок М = 200 кНм; бетон класса В15 (Rb = 8,5 МПа); арматура класса А300 (Rs = 270 МПа).
Требуется определить площадь сечения продольной арматуры.
Расчет.. ho = 600 - 40 = 560 мм. Подбор продольной арматуры производим согласно п.3.21. По формуле (3.22) вычисляем значение am
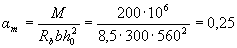
По табл. 3.2. находим ar = 0,41. Так как am = 0,25 < ar, сжатая арматура по расчету не требуется.
Требуемую площадь сечения растянутой арматуры определяем по формуле (3.23)
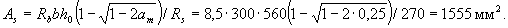
Принимаем 2Æ28 + 1Æ25 (As = 1598 мм2).
Пример 3. Дано: сечение размерами b = 300 мм, h = 800 мм; а = 70 мм; растянутая арматура А400 (Rs = 355 МПа); площадь ее сечения As = 2945 мм2 (6Æ25); бетон класса В25 (Rb = 14,5 МПа); изгибающий момент М = 550 кНм.
Требуется проверить прочность сечения.
Расчет.. ho = 800 - 70 = 730. Проверку прочности производим согласно п.3.20:
Определим значение х:
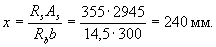
По табл. 3.2 находим ξR = 0,531. Так как 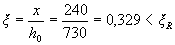 ,
,
проверяем условие (3.20):
RsAs (ho-0, 5x) = 355·2945· (730 - 0,5·240) = 636,8·106 Н мм = 636,8 кНм >M = 550кНм,
т.е. прочность сечения обеспечена.
Пример 4. Дано: сечение размерами b= 300 мм, h = 800 мм; а = 50 мм; арматура класса А400 (Rs = Rsc = 355 МПа); изгибающий момент М = 780 кНм; бетон класса В15 (Rb = 8,5 МПа).
Требуется определить площадь сечения продольной арматуры.
Расчет.. ho = h - а = 800-50=750 мм. Требуемую площадь продольной арматуры определяем согласно п.3.21. По формуле (3.22) находим значение am:
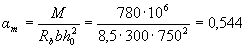
Так как am = 0,544 > ar = 0,39 (см. табл. 3.2), при заданных размерах сечения и класса бетона необходима сжатая арматура.
Принимая а' = 30 мм и ξR = 0,531 (см. табл. 3.2), по формулам (3.24) и (3.25) определим необходимую площадь сечений сжатой и растянутой арматуры:
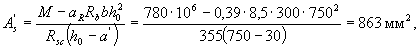
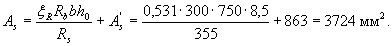
Принимаем As= 942 мм2 (3Æ20); As = 4021 мм2 (5Æ32).
Пример 5. Дано: сечение размерами b = 300 мм, h = 700 мм; а = 50 мм; а' = 30 мм; бетон класса В30 (Rb = 17 МПа); арматура А400 (Rs = Rsc = 355 МПа); площадь сечения сжатой арматуры As= 942 мм2 (3Æ20); изгибающий момент М = 580 кН м.
Требуется определить площадь сечения растянутой арматуры.
Расчет.. ho = 700 - 50 = 650 мм. Расчет производим с учетом наличия сжатой арматуры согласно п.3.22.
Вычисляем значение am:

Так как am = 0,173 < ar = 0,39 (см. табл. 3.2), необходимую площадь растянутой арматуры определяем по формуле (3.26)
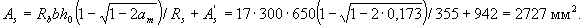
Принимаем 3Æ36 (Аs = 3054 мм2).
Пример 6. Дано: сечение размерами b = 300 мм, h = 700 мм; а = 70 мм; а' = 30 мм; бетон класса В20 (Rb =11,5 МПа); арматура класса А400 (Rs = Rsc = 355 МПа); площадь сечения растянутой арматуры As = 4826 мм2 (6Æ32), сжатой - А's= 339 мм2 (3Æ12); изгибающий момент М = 630 кН м
Требуется проверить прочность сечения.
Расчет. ho = 700 - 70 = 630 мм. Проверку прочности сечения производим согласно п.3.18.
По формуле (3.16) определяем высоту сжатой зоны х:
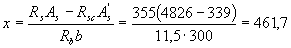
По табл. 3.2 находим ξR = 0,531 и ar = 0,39. Так как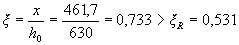 , прочность сечения проверяем из условия (3.18):
, прочность сечения проверяем из условия (3.18):
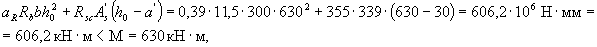 ,
,
т.е. прочность согласно этому условию не обеспечена. Уточним правую часть условия (3.18) путем замены значения ar на (0,7 ar + 0,3 am), где
am= ξ(1 - 0,5 ξ ) = 0,733(1- 0,5·0,733) = 0,464:
(0,7·0,39 + 0,3·0,464)11,5·300·6302 + 355·339·600 = 636,6·106 Н·мм = 636,6 кН·м > М = 630 кНм, т.е. прочность обеспечена.
Тавровые и двутавровые сечения
Пример 7. Дано: сечение размерами b'f = 1500 мм, h'f= 50 мм,
b = 200 мм, h = 400 мм; а = 80 мм; бетон класса В25 (Rb = 14,5 МПа), арматура класса А400 (Rs = 355 МПа); изгибающий момент М = 260 кНм.
Требуется определить площадь сечения продольной арматуры.
Расчет. hо = 400 - 80 = 320 мм. Расчет производим согласно п.3.25 в предположении, что сжатая арматура по расчету не требуется.
Проверим условие (3.32), принимая As = 0:
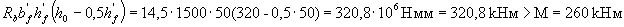 т.е. граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b = b'f =1500 мм согласно п.3.21.
т.е. граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b = b'f =1500 мм согласно п.3.21.
Вычисляем значение
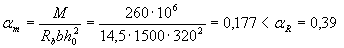 (см. табл.3.2)
(см. табл.3.2)
т.е. сжатая арматура действительно по расчету не требуется.
Площадь сечения растянутой арматуры вычисляем по формуле (3.22)
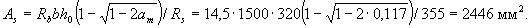
Принимаем 4Æ28 (As = 2463 мм2).
Пример 8. Дано: сечение размерами b'f = 400 мм, h'f = 120 мм, b = 200 мм, h = 600 мм; а = 65 мм; бетон класса В15 (Rb = 8,5 МПа); арматура класса А400 (Rs = 355 МПа); изгибающий момент М = 270 кНм.
Требуется определить площадь сечения растянутой арматуры.
Расчет. hо = 600 - 65 = 535 мм. Расчет производим согласно п.3.25 в предположении, что сжатая арматура по расчету не требуется.
Так как
Rbb'f h'f (ho - 0,5h'f) = 8,5·400·120(535 - 0,5·120) = 193,8·106 Н мм = 193,8 кНм >M = 270 кНм,
граница сжатой зоны проходит в ребре и площадь сечения растянутой арматуры определим по формуле (3.33), принимая площадь сечения свесов равной А0v = (b'f -b)h'f = (400 - 200) 120 = 24000 мм2. Вычисляем значение amпри A's = 0
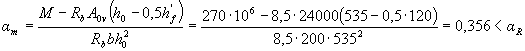 (см. табл. 3.2),
(см. табл. 3.2),
следовательно, сжатая арматура не требуется.
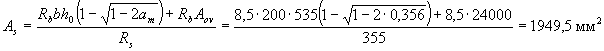
Принимаем 4Æ25(As = 1964 мм2).
Пример 9. Дано: сечение размерами b'f = 400 мм, h'f = 100 мм, b = 200 мм, h = 600 мм; а = 70 мм, бетон класса В25 (Rb = 14,5 МПа); растянутая арматура класса А400 (Rs = 355 МПа); площадь ее сечения As = 1964 мм2 (4Æ25); A's= 0,0; изгибающий момент М = 300 кНм.
Требуется проверить прочность сечения.
Расчет. hо = 600 - 70 = 530 мм. Проверку прочности производим согласно п.3.23, принимая As= 0,0. Так как Rs·As = 355·1964 = 697220 Н > Rb·b'f·h'f =14,5·400·100 = 580000 Н, граница сжатой зоны проходит в ребре, и прочность сечения проверяем из условия (3.28).
Для этого по формуле (3.29) определим высоту сжатой зоны, приняв площадь свесов равной А0v = (b'f -b)h'f = (400 - 200) ·100 = 20000 мм2:
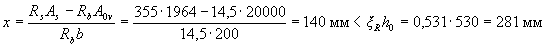
(где ξR найдено из табл. 3.2).
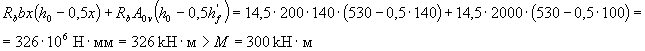 т.е. прочность сечения обеспечена.
т.е. прочность сечения обеспечена.
Элементы, работающие на косой изгиб
3.27. Расчет прямоугольных, тавровых, двутавровых и Г-образных сечений элементов, работающих на косой изгиб, допускается производить, принимая форму сжатой зоны по черт.3.5; при этом должно выполняться условие
Мх <Rb[Aweb(h0-х1/3) + Sov,x] + RscSsx, (3.35)
где Мх - составляющая изгибающего момента в плоскости оси х (за оси х и у принимаются две взаимно перпендикулярные оси, проходящие через центр тяжести сечения растянутой арматуры параллельно сторонам сечения; для сечения с полкой ось х принимается параллельно плоскости ребра);
Aweb =Аb - А0v; (3.36)
Аb - площадь сечения сжатой зоны бетона, равная
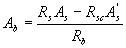 (3.37)
(3.37)
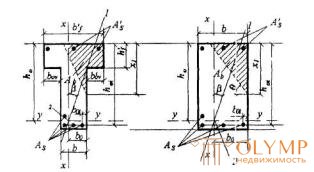
Черт.3.5 Форма сжатой зоны в поперечном сечении железобетонного элемента, работающего на косой изгиб
а - таврового сечения ; б- прямоугольного сечения; 1-плоскость действия изгибающего момента ; 2- центр тяжести сечения растянутой арматуры
А0v - площадь наиболее сжатого свеса полки;
х1 - размер сжатой зоны бетона по наиболее сжатой боковой стороне сечения, определяемый по формуле
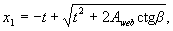 (3.38)
(3.38)
где 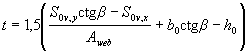
S0v,y, S0v,x - статические моменты площади Aov относительно
соответственно оси х и у;
β - угол наклона плоскости действия изгибающего момента к оси х, т.е. ctg β = Mx/My (My - составляющая изгибающего момента в плоскости оси у);
bо - расстояние от центра тяжести сечения растянутой арматуры до наиболее сжатой боковой грани ребра (стороны).
При расчете прямоугольных сечений значения Aov, S0v,y, S0v,x принимаются равными нулю.
Если Аb < Aov или х1 < 0,2h'f, расчет производится как для прямоугольного сечения шириной b = b'f. Если выполняется условие
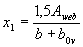 (3.39)
(3.39)
(где b0v - ширина наименее сжатого свеса полки),
расчет производится без учета косого изгиба, т.е. по формулам пп. 3.18 и 3.23 на действие момента М = Мх, при этом следует проверить условие (3.40), принимая х1 как при косом изгибе.
При определении значения Аb по формуле (3.37) напряжение в растянутом стержне, ближайшем к границе сжатой зоны, не должно быть менее Rs, что обеспечивается соблюдением условия
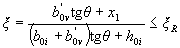 (3.40)
(3.40)
где ξR - см. табл. 3.2;
b0i и h0i - расстояния от рассматриваемого стержня соответственно до наиболее сжатой грани (стороны) и до наиболее сжатой грани, нормальной к оси х (см. черт.3.5);
b'ov - ширина наиболее сжатого свеса;
θ - угол наклона прямой, ограничивающей сжатую зону, к оси y; значение tgθ определяется по формуле
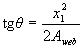
Если условие (3.40) не соблюдается, расчет сечения производится последовательными приближениями, заменяя в формуле (3.37) для каждого растянутого стержня величину Rs значениями напряжений равными
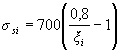 (МПа), но не более Rs.
(МПа), но не более Rs.
При проектировании конструкций не рекомендуется допускать превышение значения ξi над ξR более чем на 20%, при этом можно провести только один повторный расчет с заменой в формуле (3.37) значений Rs для растянутых стержней, для которых ξi > ξR , на напряжения, равные
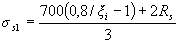 (3.41)
(3.41)
При пользовании формулой (3.37) за растянутую арматуру площадью As рекомендуется принимать арматуру, располагаемую вблизи растянутой грани, параллельной оси у, а за сжатую арматуру площадью As - арматуру, располагаемую вблизи сжатой грани, параллельно оси у, но по одну наиболее сжатую сторону от оси x: (см. черт.3.5).
Настоящим пунктом можно пользоваться, если выполняется условие:
для прямоугольных, тавровых и Г-образных сечений с полкой в сжатой зоне х1 < h;
для двутавровых, тавровых и Г-образных сечений с полкой в растянутой зоне х1 < h - hf – bov,t tg θ,
где hf и bov,t - высота и ширина наименее растянутого свеса полки (черт.3.6).
В противном случае расчет производится на основе нелинейной деформационной модели согласно пп.3.72 - 3.76, принимая N = 0.
3.28. Требуемое количество растянутой арматуры при косом изгибе для элементов прямоугольного, таврового и Г-образного сечений с полкой в сжатой зоне рекомендуется определять с помощью графиков на черт.3.7. Для этого ориентировочно задаются положением центра тяжести сечения растянутой арматуры и по графику определяют значения as в зависимости от:
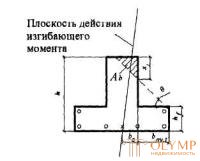
Черт.3.6. Тавровое сечение со сжатой зоной, заходящей в наименее растянутый свес полки
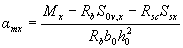
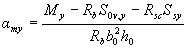
где Ssx и Ssy - статические моменты площади As относительно соответственно оси y и оси х.
Остальные обозначения - см. п.3.27.
Если атх < 0, расчет производится как для прямоугольного сечения, принимая b = b'f.
Если значение as на графике находится по левую сторону от кривой, отвечающей параметру 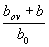 , подбор арматуры производится без учета косого изгиба, т.е. согласно пп.3.22 и 3.26 на действие момента М = Мх.
, подбор арматуры производится без учета косого изгиба, т.е. согласно пп.3.22 и 3.26 на действие момента М = Мх.
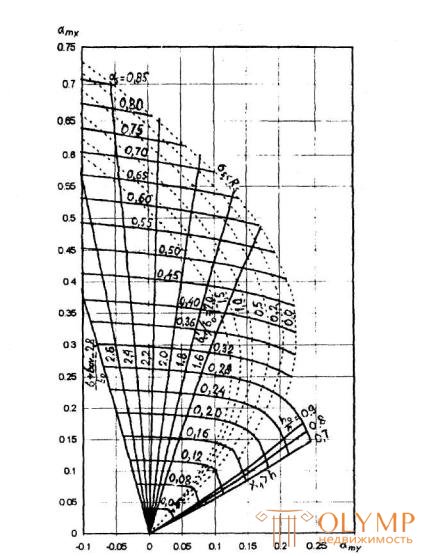
Черт.3.7. График несущей способности прямоугольного, таврового и Г-образного сечений для элементов, работающих на косой изгиб
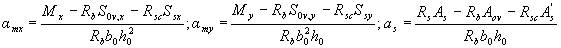
Требуемая площадь растянутой арматуры при условии ее работы с полным расчетным сопротивлением определяется по формуле
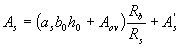 (3.42)
(3.42)
где Aov - см. формулу (3.36).
Центр тяжести фактически принятой растянутой арматуры должен отстоять от растянутой грани не дальше, чем принятый в расчете центр тяжести. В противном случае расчет повторяют, принимая новый центр тяжести сечения растянутой арматуры.
Условием работы растянутой арматуры с полным сопротивлением является выполнение условия (3.40). При арматуре класса А400 и ниже условие (3.40) всегда выполняется, если значение as на графике 3.7 находится внутри области, ограниченной осями координат, и кривой, отвечающей параметру b'ov/bo
Если условие (3.40) не выполняется, следует поставить (увеличить) сжатую арматуру, либо повысить класс бетона, либо увеличить размеры сечения (особенно наиболее сжатого свеса полки).
Значения as на графике не должны находиться между осью amy, и кривой, соответствующей параметру ho/h. В противном случае х1 становится более h, и расчет тогда следует производить согласно пп.3.72 - 3.76.
Примеры расчета
Пример 10. Дано: железобетонный прогон кровли с уклоном 1:4 (ctgβ = 4); сечение и расположение арматуры - по черт.3.8; бетон класса В25 (Rb =14,5МПа); растянутая арматура класса А400 (Rs = 355МПа); As = 763 мм2 (3Æ18);A's= 0,0; изгибающий момент в вертикальной плоскости M = 82,6 кНм.
Требуется проверить прочность сечения.
Ра с ч е т. Из черт.3.8 следует:
ho = 400-30-(1·30/3)=360 мм; bo = (2·120+1·30)/3=90 мм; b'ov = bov = (300-150)/2=75 мм;
h'f = 80+20/2=90 мм.
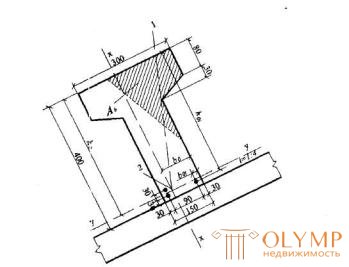
Черт.3.8 К примеру расчета 10
1 -плоскость действия изгибающего момента; 2-центр тяжести сечения растянутой арматуры
По формуле (3.37) определим площадь сжатой зоны бетона Аb
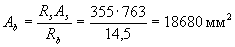
Площадь наиболее сжатого свеса полки и статические моменты этой площади относительно х и у соответственно равны:
Aov= b'ov h'f = 75·90 = 6750 мм2;
Sov,y = Aov(b0 + b'ov /2)=6750(90 + 75/2) = 86,06·104мм3;
Sov,x = Aov(h0 - h'f /2) = 6750(360 - 90/2) = 212,6·104мм3.
Так как Аb > Aov, расчет продолжаем как для таврового сечения.
Aweb = 18680 - 6750 = 11930 мм2.
Определим по формуле (3.38) размер сжатой зоны х1. Для этого вычисляем
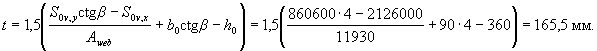
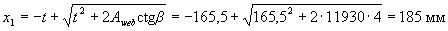
Проверим условие (3.39):
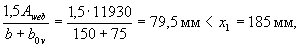
следовательно, расчет продолжаем по формулам косого изгиба.
Проверим условие (3.40) для наименее растянутого стержня. Из черт.3.8 имеем boi = 30 мм, hoi = 400 - 30 = 370 мм;
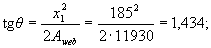
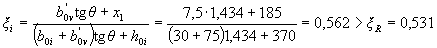 (см. табл. 3.2).
(см. табл. 3.2).
Условие (3.40) не соблюдается. Расчет повторим, заменяя в формуле (3.37) значение Rs для наименее растянутого стержня напряжением σS определенным по формуле (3.41), и корректируя значения ho и bо.
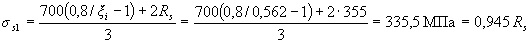
Поскольку все стержни одинакового диаметра, новые значения Ao, ho и bо будут равны:
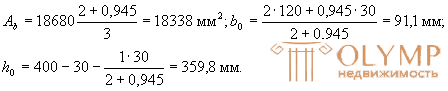
Аналогично определим значения Sov,y, Sov,x, Aweb и x1:
Sov,y = 6750· (91,1 + 75/2) = 86,8·104мм3;
Sov,x = 6750· (359,8 - 90/2) = 212,5·104мм3;
Aweb = 18338 - 6750 = 11588 мм2;
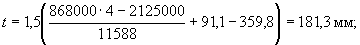
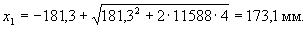
Проверяем прочность сечения из условия (3.35), принимая Ssx=0 и

Rb[Aweb(h0-х1/3) + Sov,x] = 14,5[11588(359,8-173,1/3)+212,5·104] = 81,57·106 Н·мм > Mx = 80,1·106 Н·мм
т.е. прочность сечения обеспечена.
Пример 11. По данным примера 10 необходимо подобрать площадь растянутой арматуры при моменте в вертикальной плоскости M = 64кНм.
Расчет. Составляющие изгибающего момента в плоскости осей у и х равны:
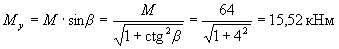
Mx =Myctgβ = 15,52·4 = 62,1 кНм.
Определим необходимое количество арматуры согласно п.3.28.
Принимая значения Rb, ho, Sov,x и Sov,y из примера 10 при Ssy = Ssx = 0 находим значения aтх и amy:
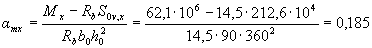
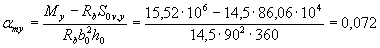
Так как aтх > 0, расчет продолжаем для таврового сечения.
Поскольку точка с координатами aтх = 0,185 и amy = 0,072 на графике черт.3.7 находится по правую сторону от кривой, отвечающей параметру 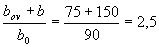 , и по левую сторону от кривой, отвечающей параметру b'ov/bov = 75 / 90 = 0,83, расчет продолжаем с учетом косого изгиба и полного расчетного сопротивления арматуры, т.е. условие (3.40) выполнено.
, и по левую сторону от кривой, отвечающей параметру b'ov/bov = 75 / 90 = 0,83, расчет продолжаем с учетом косого изгиба и полного расчетного сопротивления арматуры, т.е. условие (3.40) выполнено.
На графике координатам aтх = 0,185 и amy = 0,072 соответствует значение as = 0,20. Тогда согласно формуле (3.42) площадь сечения растянутой арматуры будет равна
Аs = (as boho + Aov)Rb/Rs= (0,2·90·360 + 6750)14,5/355 = 540,4 мм2.
Принимаем стержни 3Æ16 (Аs = 603 мм2) и располагаем их, как показано на черт.3.8.
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПРИ ДЕЙСТВИИ ПОПЕРЕЧНЫХ СИЛ
3.29. Расчет элементов при действии поперечных сил должен обеспечить прочность:
- по полосе между наклонными сечениями согласно п.3.30;
- на действие поперечной силы по наклонному сечению согласно пп.3.31- 3.42;
- на действие момента по наклонному сечению согласно пп.3.43-3.48.
Расчет железобетонных элементов по полосе между наклонными сечениями
3.30. Расчет изгибаемых элементов по бетонной полосе между наклонными сечениями производят из условия
Q < 0,3Rbbho, (3.43)
где Q - поперечная сила в нормальном сечении, принимаемая на расстоянии от опоры не менее ho.
Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил
Элементы постоянной высоты, армированные хомутами, нормальными к оси элемента
3.31. Расчет изгибаемых элементов по наклонному сечению (черт.3.9) производят из условия
Q < Qb + Qsw, (3.44)
где Q - поперечная сила в наклонном сечении с длиной проекции с от внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем на расстоянии с от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длиной с;
Qb - поперечная сила, воспринимаемая бетоном в наклонном сечении;
Qsw - поперечная сила, воспринимаемая хомутами в наклонном сечении.
Поперечную силу Qb определяют по формуле
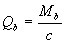 (3.45)
(3.45)
где
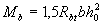 (3.46)
(3.46)
Значение Qb принимают не более 2,5Rbtbho и не менее 0,5Rbtbho.
Значение с определяют согласно п.3.32.
Усилие Qsw определяют по формуле
Qsw= 0,75 qsw co, (3.47)
где qsw - усилие в хомутах на единицу длины элемента, равное
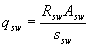 (3.48)
(3.48)
cо - длина проекции наклонной трещины, принимаемая равной с, но не более 2ho.
Хомуты учитывают в расчете, если соблюдается условие
qsw > 0,25Rbtb (3.49)
Можно не выполнять это условие, если в формуле (3.46) учитывать такое уменьшенное значение Rbtb, при котором условие (3.49) превращается в равенство, т.е. принимать 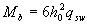
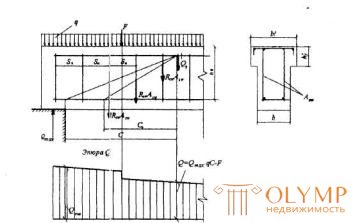
Черт.3.9. Схема усилий в наклонном сечении элементов с хомутами при расчете его на действие поперечной силы
3.32. При проверке условия (3.44) в общем случае задаются рядом наклонных сечений при различных значениях с, не превышающих расстояние от опоры до сечения с максимальным изгибающим моментом и не более 3ho
При действии на элемент сосредоточенных сил значения с принимают равными расстояниям от опоры до точек приложения этих сил (черт.3.10), а также равными 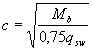 но не меньше h0, если это значение меньше расстояния от опоры до 1-го груза.
но не меньше h0, если это значение меньше расстояния от опоры до 1-го груза.
При расчете элемента на действие равномерно распределенной нагрузки q невыгоднейшее значение с принимают равным 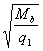 , а если при этом
, а если при этом 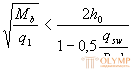 или
или 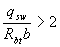 , следует принимать
, следует принимать 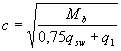 , где значение q1 определяют следующим образом:
, где значение q1 определяют следующим образом:
а) если действует сплошная равномерно распределенная нагрузка q, q1 = q;
б) если нагрузка q включает в себя временную нагрузку, которая приводится к эквивалентной по моменту равномерно распределенной нагрузке qv (т.е. когда эпюра моментов М от принятой в расчете нагрузки qv всегда огибает эпюру М от любой фактической временной нагрузки), q1 = q - 0,5 qv.
При этом в условии (3.44) значение Q принимают равным Qmax - q1с, где Qmax - поперечная сила в опорном сечении.
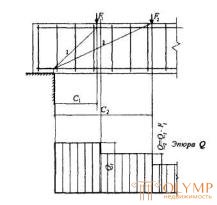
Черт.3.10. Расположение расчетных наклонных сечений при сосредоточенных силах
1 - наклонное сечение проверяемое на действие поперечной силы Q1; 2 – то же, силы Q2
3.33. Требуемая интенсивность хомутов, выражаемая через qsw (см. п.3.31), определяется следующим образом:
а) при действии на элемент сосредоточенных сил, располагаемых на расстояниях сi от опоры, для каждого i-го наклонного сечения с длиной проекции сi не превышающей расстояния до сечения с максимальным изгибающим моментом, значение qsw(i) определяется следующим образом в зависимости от коэффициента аi = сi /ho, принимаемого не более 3:
если
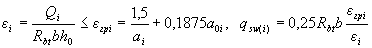 (3.50)
(3.50)
если
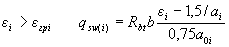 (3.51)
(3.51)
где а0i - меньшее из значений аi и 2;
Qi - поперечная сила в i-ом нормальном сечении, расположенном на расстоянии сi от опоры;
окончательно принимается наибольшее значение qsw,
б) при действии на элемент только равномерно распределенной нагрузки q требуемая интенсивность хомутов qswопределяется в зависимости от 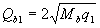 следующим образом:
следующим образом:
если Qbi ≥ 2Mb/ho - Qmax
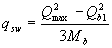 ; (3.52)
; (3.52)
если Qbi < 2Mb/ho - Qmax.
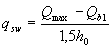 ; (3.53)
; (3.53)
при этом, если Qbl < Rbtbho,
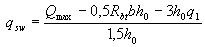 , (3.54)
, (3.54)
где Mb, - см. п.3.31; q1 -см. п.3.32.
В случае, если полученное значение qsw не удовлетворяет условию (3.49), его следует вычислять по формуле
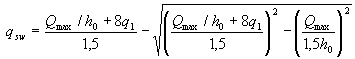 (3.55)
(3.55)
и принимать не менее 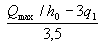 .
.
3.34. При уменьшении интенсивности хомутов от опоры к пролету с qsw1 до qsw2 (например, увеличением шага хомутов) следует проверить условие (3.44) при значениях с, превышающих l1 - длину участка с интенсивностью хомутов qsw1 (черт.3.11). При этом значение Qsw принимается равным:
если с < 2ho + l1,
Qsw = 0,75[qsw1co- (qsw1 - qsw2)(c - l1)]; (3.56)
если с > 2ho + l1,
Qsw = 1,5qsw2ho, (3.57)
co -см. п.3.31.
При действии на элемент равномерно распределенной нагрузки длина участка с интенсивностью хомутов qsw1принимается не менее значения l1, определяемого в зависимости от Δqsw = 0,75(qsw1 - qsw2) следующим образом:
- если Δqsw < q1,
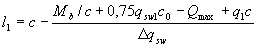 (3.58)
(3.58)
где 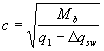 , но не более 3hо
, но не более 3hо
при этом, если 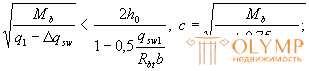
- если Δqsw ≥ q1
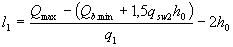 (3.59)
(3.59)
здесь Мb, c0 -см. п.3.31; q1- см. п.3.32;
Qb.min = 0,5Rbtbho
Если для значения qsw2 не выполняется условие (3.49), длина l1 вычисляется при скорректированных согласно п.3.31 значениях 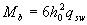 и Qb.min = 2hoqsw2; при этом сумма (Qb.min + 1,5qswho) в формуле (3.59) принимается не менее нескорректированного значения Qb.min
и Qb.min = 2hoqsw2; при этом сумма (Qb.min + 1,5qswho) в формуле (3.59) принимается не менее нескорректированного значения Qb.min
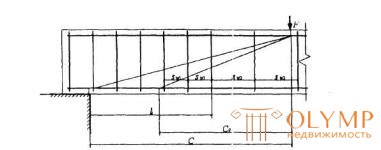
Черт.3.11. К расчету наклонных сечений при изменении интенсивности хомутов
3.35. Шаг хомутов, учитываемых в расчете, должен быть не более значения:
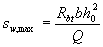 (3.60)
(3.60)
Кроме того, хомуты должны отвечать конструктивным требованиям, приведенным в пп.5.20 и 5.21.
Элементы переменной высоты с поперечным армированием
3.36. Расчет элементов с наклонными на приопорных участках сжатыми или растянутыми гранями производят согласно п.3.31, принимая в качестве рабочей высоты сечения наибольшее значение ho в пределах рассматриваемого наклонного сечения (черт.3.12).
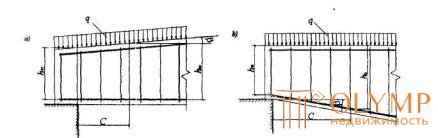
Черт.3.12 Балки с переменной высотой сечения и наклонной гранью
3.37. Для балок без отгибов высотой, равномерно увеличивающейся от опоры к пролету, рассчитываемых на действие равномерно распределенной нагрузки q, наклонное сечение проверяют из условия (3.44) при невыгоднейшем значении с, равном
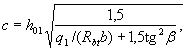 (3.61)
(3.61)
при этом, если это значение с меньше 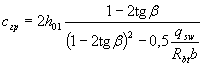 или,
или,
если 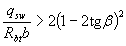 , то невыгоднейшее значение с равно
, то невыгоднейшее значение с равно
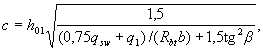 (3.62)
(3.62)
Принятое значение с не должно превышать 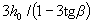 , а также длину участка балки с постоянным значением β.
, а также длину участка балки с постоянным значением β.
Здесь: ho1 - рабочая высота опорного сечения балки;
q1 -см. п.3.32;
β - угол между сжатой и растянутой гранями балки.
Рабочую высоту принимают равной ho = ho1+ с·tg β.
При уменьшении интенсивности хомутов от qsw1 у опоры до qsw2 в пролете следует проверить условие (3.44) при значениях с, превышающих l1 - длину участка элемента с интенсивностью хомутов qsw1; при этом значение Qswопределяют по формуле (3.56) либо по формуле (3.57) п.3.34 в зависимости от выполнения или невыполнения условия 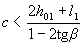 .
.
При действии на балку сосредоточенных сил, значение с принимают равным расстоянию от опоры до точек приложения этих сил, а также определяют по формуле (3.62) при q1 = 0, если это значение с меньше расстояния от опоры до 1-го груза.
3.38. Для консолей без отгибов высотой, равномерно увеличивающейся от свободного конца к опоре (черт.3.13), в общем случае проверяют условие (3.44), задаваясь наклонными сечениями со значениями с, определяемыми по формуле (3.62) при q1 = 0 и принимаемыми не более расстояния от начала наклонного сечения в растянутой зоне до опоры. При этом за ho1 и Q принимают соответственно рабочую высоту и поперечную силу в начале наклонного сечения в растянутой зоне. Кроме того, если с >2ho1/(1-2tgβ), проверяют наклонные сечения, проведенные до опоры.
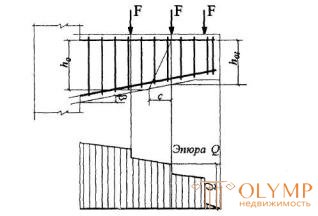
Черт.3.13. Консоль высотой, уменьшающейся от опоры к свободному концу
При действии на консоль сосредоточенных сил начало наклонного сечения располагают в растянутой зоне нормальных сечений, проведенных через точки приложения этих сил (см. черт.3.13).
При действии равномерно распределенной нагрузки или нагрузки, линейно увеличивающейся к опоре, консоль рассчитывают как элемент с постоянной высотой сечения согласно п.3.31 и п.3.32, принимая рабочую высоту hо в опорном сечении.
Элементы, армированные отгибами
3.39. Проверку прочности наклонного сечения на действие поперечной силы для элемента с отгибами производят из условия (3.44) с добавлением к правой его части значения
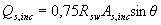 (3.63)
(3.63)
где Аs,inc - площадь сечения отгибов, пересекающих наклонную трещину, расположенную у конца наклонного сечения с длиной проекции равной с, но не более 2ho (черт.3.14);
θ - угол наклона отгибов к продольной оси элемента.
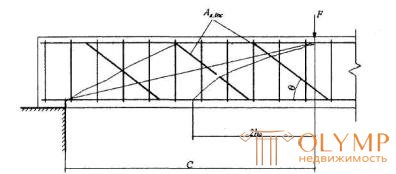
Черт.3.14. К определению наиболее опасной наклонной трещины для элементов с отгибами при расчете на действие поперечной силы
Значения с принимают равным расстояниям от опоры до концов отгибов, а также до мест приложения сосредоточенных сил; кроме того, следует проверить наклонные сечения, заканчивающиеся на расстоянии 2ho от начала предпоследней и последней плоскости отгибов (черт.3.15).
3.40. Расстояния между опорой и концом отгиба, ближайшего к опоре s1 также между концом предыдущей и началом последующего отгибов s2 (черт.3.16) должно быть не более 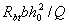 .
.
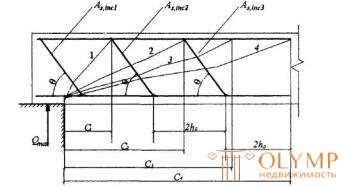
Черт.3.15. К определению наклонных сечений в элементе с отгибами
1-4- расчетные наклонные сечения
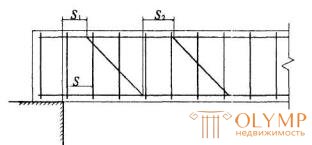
Черт.3.16. Расстояния между хомутами, опорой и отгибами
Кроме того, отгибы должны удовлетворять конструктивным требованиям, приведенным в п.5.22.
Элементы без поперечной арматуры
3.41. Расчет элементов без поперечной арматуры на действие поперечной силы производится из условий
a)
Qmax< 2,5Rbtbho (3.64)
где Qmax - максимальная поперечная сила у грани опоры;
6)
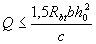 (3.65)
(3.65)
где Q - поперечная сила в конце наклонного сечения, начинающегося от опоры; значение с принимается не более сmax = 3ho.
Для сплошных плоских плит с несвободными краями (соединенными с другими элементами или имеющими опоры) и шириной b > 5h допускается принимать стах= 2,4ho.
При действии на элемент сосредоточенных сил значения с принимаются равными расстояниям от опоры до точек приложения этих сил (черт.3.17), но не более стах.
При расчете элемента на действие распределенных нагрузок, если выполняется условие
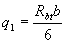 , (3.66)
, (3.66)
условие (3.65) принимает вид
Qmax< 0,5Rbtbho + 3hoq1 (3.67)
(что соответствует с = 3ho),
а при невыполнении условия (3.66) - 
(что соответствует 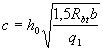 ).
).
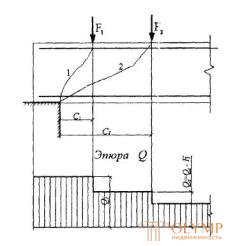
Черт.3.17. Расположение невыгоднейших наклонных сечений в элементах без поперечной арматуры
1- наклонное сечение, проверяемое на действие поперечной силы Q1; 2- то же, силы Q2
Для упомянутых плоских плит с несвободными боковыми краями правая часть условия (3.66) делится на 0,64, а условие (3.67) принимает вид
Qmax≤ 0,625Rbtbho + 2,4hoq1. (3.67a)
Здесь q1 принимается при действии равномерно распределенной нагрузки в соответствии с п.3.32, а при действии сплошной нагрузки с линейно изменяющейся интенсивностью - равной средней интенсивности на приопорном участке длиной, равной четверти пролета балки (плиты) или половины вылета консоли, но не более стах.
3.42. Для элементов с переменной высотой сечения при проверке условия (3.64) значение ho принимается в опорном сечении, а при проверке условия (3.65) - как среднее значение ho в пределах наклонного сечения.
Для элементов с высотой сечения, увеличивающейся с увеличением поперечной силы значение сmахпринимается равным 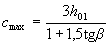 , а для плоских плит, указанных в п.3.41, -
, а для плоских плит, указанных в п.3.41, -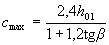
где ho1 - рабочая высота в опорном сечении;
β - угол между растянутой и сжатой гранями.
При действии на такой элемент распределенной нагрузки значение с в условии (3.65) принимается равным
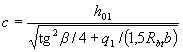 (3.68)
(3.68)
но не более стах где q1 - см. п.3.32.
Расчет железобетонных элементов по наклонным сечениям на действие моментов
3.43. Расчет железобетонных элементов по наклонным сечениям на действие момента (черт.3.18) производят из условия
M ≤ Ms + Msw, (3.69)
где М - момент в наклонном сечении с длиной проекции с на продольную ось элемента, определяемый от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения, относительно конца наклонного сечения (точка 0), противоположного концу, у которого располагается проверяемая продольная арматура, испытывающая растяжение от момента в наклонном сечении (черт.3.19)
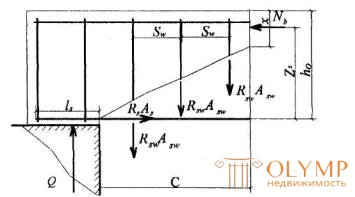
Черт.3.18. Схема усилий в наклонном сечении при расчете его по изгибающему моменту
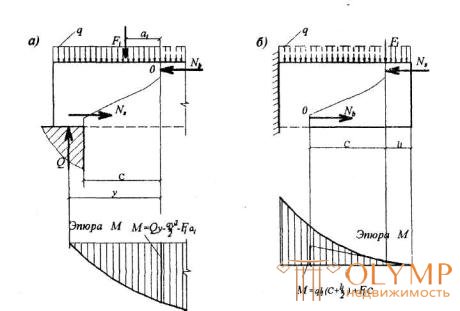
Черт.3.19. Определение расчетного значения момента при расчете наклонного сечения
а - для свободно опертой балки; б - для консоли
Ms - момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения;
Msw- момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка 0).
Момент Ms, определяют по формуле
Ms = Ns·zs, (3.70)
где Ns - усилие в продольной растянутой арматуре, принимаемое равным RsAs, а в зоне анкеровки определяемое согласно п.3.45;
zs - плечо внутренней пары сил, определяемое по формуле
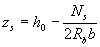 (где b - ширина сжатой грани);
(где b - ширина сжатой грани);
но при наличии сжатой арматуры принимаемое не менее ho - a'; допускается также принимать zs = 0,9ho.
Момент Msw при поперечной арматуре в виде хомутов, нормальных к продольной оси элемента, определяют по формуле
Msw =0,5 qsw c2 (3.71)
где qsw определяют по формуле (3.48) п.3.31, а с принимают не более 2ho.
Если хомуты в пределах длины с меняют свою интенсивность с qsw у начала наклонного сечения на qsw2, момент Msw определяют по формуле:
Msw =0,5 qsw1 c2-0,5(qsw1 - qsw2)(c - l1)2 (3.72)
где l1 - длина участка с интенсивностью хомутов qsw1.
Значение с определяют согласно п.3.46.
3.44. Расчет на действие момента производят для наклонных сечений, расположенных в местах обрыва продольной арматуры, а также у грани крайней свободной опоры балок и у свободного конца консолей при отсутствии у продольной арматуры специальных анкеров.
Кроме того, рассчитываются наклонные сечения в местах резкого изменения высоты элемента (например, в подрезках).
3.45. При пересечении наклонного сечения с продольной растянутой арматурой, не имеющей анкеров в пределах зоны анкеровки, усилие Ns определяется по формуле:
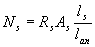 (3.73)
(3.73)
где ls - расстояние от конца арматуры до точки пересечения с ней наклонного сечения;
1ап- длина зоны анкеровки, равная 1ап= λапds
где
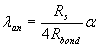 (3.74)
(3.74)
Rbond - расчетное сопротивление сцепления арматуры с бетоном, равное
Rbond = η1 η2Rbt
η1 - коэффициент, учитывающий влияние вида поверхности арматуры и принимаемый равным:
2,5 - для арматуры классов А300, А400, А500;
2,0 - для арматуры класса В500;
1,5 - для арматуры класса А240;
η2 - коэффициент, учитывающий влияние диаметра арматуры и принимаемый равным:
1,0 - при диаметре ds <32 мм,
0,9 - при диаметрах 36 и 40 мм;
а - коэффициент, учитывающий влияние поперечного обжатия бетона и поперечной арматуры и принимаемый равным:
а) для крайних свободных опор,
если 0,25 ≤ σb/Rb ≤ 0,75 - 0,75;
если σb/Rb < 0,25 или σb/Rb > 0,75 - 1,0,
здесь σb= Fsup/Asup;
Fsup, Asup - опорная реакция и площадь опирания балки;
при этом если имеется поперечная арматура, охватывающая без приварки продольную арматуру, коэффициент а делится на величину 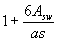 (где Asw и s - площадь сечения огибающего хомута и его шаг) и принимается не менее 0,7;
(где Asw и s - площадь сечения огибающего хомута и его шаг) и принимается не менее 0,7;
б) для свободных концов консоли - 1,0.
В любом случае коэффициент λап принимается не менее 15, а длина зоны анкеровки 1ап принимается не менее 200 мм.
Для стержней диаметром менее 36 мм значение λап можно принимать по табл.3.3.
В случае приваривания к продольным растянутым стержням поперечной или распределительной арматуры усилие Ns увеличивается на величину
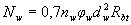 , (3.75)
, (3.75)
принимаемую не более 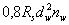 .
.
Здесь:
nw - количество приваренных стержней по длине ls;
φw - коэффициент, принимаемый по табл.3.4;
dw - диаметр припариваемых стержней.
При этом значение Ns принимается не более значения, вычисленного по формуле (3.73) с использованием при определении 1апкоэффициента, а = 0,7.
При устройстве на концах стержней специальных анкеров в виде пластин, шайб, гаек, уголков, высаженных головок и т.п., удовлетворяющих требованиям п.5.35, а также при приварке концов стержней к надежно заанкеренным закладным деталям усилие Ns принимается равным RsAs.
3.46. Для свободно опертых балок невыгоднейшее наклонное сечение начинается от грани опоры и имеет проекцию с, принимаемую не более 2ho и определяемую следующим образом:
Таблица 3.3
|
Класс арматуры |
Коэффициент а |
Относительная длина анкеровки арматуры λап = lan/ds при бетоне классов |
||||||||||
|
В10 |
В15 |
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
В55 |
В60 |
||
|
А240 |
0,7 |
45 |
33 |
28 |
24 |
22 |
19 |
18 |
17 |
16 |
15 |
15 |
|
0,75 |
48 |
36 |
36 |
26 |
23 |
21 |
19 |
18 |
17 |
16 |
15 |
|
|
1,0 |
64 |
48 |
40 |
34 |
31 |
28 |
26 |
24 |
22 |
21 |
20 |
|
|
А300 |
0,7 |
34 |
25 |
21 |
18 |
16 |
15 |
15 |
15 |
15 |
15 |
15 |
|
0,75 |
36 |
27 |
23 |
19 |
18 |
16 |
15 |
15 |
15 |
15 |
15 |
|
|
1,0 |
48 |
36 |
30 |
26 |
23 |
21 |
19 |
18 |
17 |
16 |
15 |
|
|
А400 |
0,7 |
44 |
33 |
28 |
24 |
22 |
19 |
18 |
17 |
16 |
15 |
15 |
|
0,75 |
48 |
36 |
30 |
25 |
23 |
20 |
19 |
18 |
17 |
16 |
15 |
|
|
1,0 |
63 |
47 |
39 |
34 |
31 |
27 |
25 |
24 |
22 |
21 |
20 |
|
|
А500 |
0,7 |
54 |
41 |
34 |
29 |
26 |
23 |
22 |
20 |
19 |
18 |
17 |
|
0,75 |
58 |
44 |
36 |
31 |
28 |
25 |
23 |
22 |
20 |
19 |
18 |
|
|
1,0 |
78 |
58 |
48 |
41 |
38 |
33 |
31 |
29 |
27 |
26 |
24 |
|
|
В500 |
0,7 |
65 |
48 |
40 |
35 |
32 |
28 |
26 |
24 |
23 |
21 |
20 |
|
0,75 |
69 |
52 |
43 |
37 |
34 |
30 |
28 |
26 |
24 |
23 |
22 |
|
|
1,0 |
93 |
69 |
58 |
49 |
45 |
40 |
37 |
35 |
32 |
31 |
29 |
|
|
Примечание. При расчете с учетом только постоянных и длительных нагрузок значения λап следует делить на γbl - 0,9. |
||||||||||||
Таблица 3.4.
|
dw |
6 |
8 |
10 |
12 |
14 |
|
φw |
200 |
150 |
120 |
100 |
80 |
а) если на элемент действуют сосредоточенные силы, значения с принимаются равными расстояниям от опоры до точек приложения этих сил, а также равным Qmax/qsw, если это значение меньше расстояния до 1-го груза;
б) если на элемент действует равномерно распределенная нагрузка q, значение с определяется по формуле:
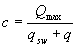 , (3.76)
, (3.76)
здесь qsw - см. формулу (3.48).
Если хомуты в пределах длины с меняют свою интенсивность с qsw1 у начала наклонного сечения на qsw2, значение с определяется по формуле (3.76) при уменьшении числителя на Δqswl1 а знаменателя - на Δqsw, (где l1 - длина участка с интенсивностью qsw1, Δqsw1 = qsw1- qsw2)
Для балок с наклонной сжатой гранью при действии равномерно распределенной нагрузки проверяют наклонные сечения со значениями с, равными
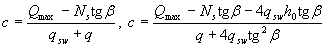 (3.77)
(3.77)
где ho - рабочая высота в опорном сечении;
β - угол наклона сжатой грани к горизонтали.
При растянутой грани, наклоненной под углом β к горизонтали, в этих формулах значение tg β заменяется на sin β.
Для консолей, нагруженных сосредоточенными силами (черт.3.19,б) проверяются наклонные сечения, начинающиеся у мест приложения сосредоточенных сил вблизи свободного конца со значениями с = Q1/qsw (где Q1 - поперечная сила в начале наклонного сечения), но не более l1 - расстояния от начала наклонного сечения до опоры. При этом, если Q1/qsw > 2ho, следует принимать с = l1. Если такие консоли имеют наклонную сжатую грань, значение Q1/qsw заменяется на (Q1 - Nstg β)/qsw.
Для консолей, нагруженных только равномерно распределенной нагрузкой q, невыгоднейшее сечение заканчивается в опорном сечении и имеет длину проекции
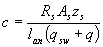 (3.78)
(3.78)
но не более 2ho.
В случае, если с < l - lan , расчет наклонного сечения можно не производить.
Здесь: As – площадь сечения арматуры, доводимой до свободного конца; zs - см. п.3.43; lan- см. п.3.45.
При отсутствии поперечной арматуры значение с принимают равным 2ho, где ho - рабочая высота в конце наклонного сечения.
3.47. Для обеспечения прочности наклонных сечений на действие момента в элементах постоянной высоты с хомутами продольные растянутые стержни, обрываемые в пролете, должны заводиться за точку теоретического обрыва (т.е. за нормальное сечение, в котором внешний момент становится равным предельному моменту Мultбез учета обрываемой арматуры, черт.3.20) на длину не менее величины w, определяемой по формуле
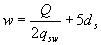 (3.79)
(3.79)
при этом, если 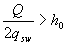
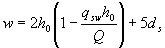 , (3.80)
, (3.80)
где Q - поперечная сила в нормальном сечении, проходящем через точку теоретического обрыва;
qsw – см. п.3.31;
ds - диаметр обрываемого стержня.
Для балки с наклонной сжатой гранью при tg β ≤ 0,2 величина w принимается равной
w = aho + 5ds, (3.81)
при этом, если а >1,
w = ho(2,2 - 1,2/а) + 5ds, (3.82)
где 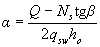
β - угол наклона грани к горизонтали.
Для балки с наклонной растянутой гранью w определяется аналогично с заменой tg β на sin β.
Для элементов без поперечной арматуры значение w принимают равным 2hо.
Кроме того, должны быть учтены требования пп.5.32 и 5.33.
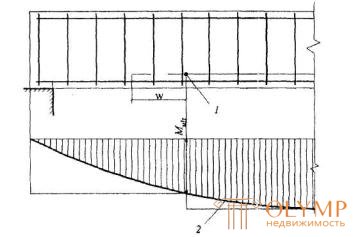
Черт.3.20. Обрыв растянутых стержней в пролете
1- точка теоретического обрыва;2- эпюра М
3.48. Для обеспечения прочности наклонных сечений на действие момента начало отгиба в растянутой зоне должно отстоять от нормального сечения, в котором отгибаемый стержень полностью используется по моменту, не менее, чем на 0,5ho, а конец отгиба должен быть расположен не ближе того нормального сечения, в котором отгиб не требуется по расчету (черт.3.21).
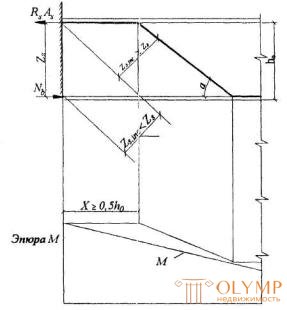
Черт. 3.21. К определению места отгиба продольной растянутой арматуры
Примеры расчета
Расчет наклонных сечений на действие поперечных сил
Пример 12. Дано: ребро ТТ-образной плиты перекрытия с размерами сечения: h = 350 мм, d = 85 мм; а = 35 мм; бетон класса В15 (Rb = 8,5 МПа, Rbt = 0,75 МПа); ребро армировано плоским каркасом с поперечными стержнями из арматуры класса А400 (Rsw = 285 МПа) диаметром 8 мм (Asw = 50,3 мм2) шагом sw - 100 мм; полная равномерно распределенная нагрузка, действующая на ребро, q = 21,9 кН/м; временная эквивалентная нагрузка qv = 18 кН/м; поперечная сила на опоре Qmax = 62 кН.
Требуется проверить прочность наклонных сечений и бетонной полосы между наклонными сечениями.
Расчет. ho = h - a = 350-35 = 315 мм.
Прочность бетонной полосы проверим из условия (3.43):
0,3Rbbh0 = 0,3·8,5·85·315 = 68276 Н > Qmax = 62 кН, т.е. прочность полосы обеспечена.
Прочность наклонного сечения по поперечной силе проверим согласно п.3.31.
По формуле (3.48) определим интенсивность хомутов
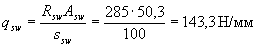
Поскольку 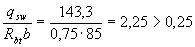 , т.е. условие (3.49) выполнено, хомуты полностью учитываем и значение Мb определяем по формуле (3.46)
, т.е. условие (3.49) выполнено, хомуты полностью учитываем и значение Мb определяем по формуле (3.46)
Мb = 1,5Rbtbh02= 1,5·0,75·85·3152 = 9,488·106 Н·мм.
Согласно п.3.32 определим длину проекции невыгоднейшего наклонного сечения с.
q1 = q - qv/2 = 21,9 - 18/2 = 12,9 кН/м (Н/мм).
Поскольку 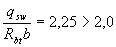 , значение с определяем по формуле
, значение с определяем по формуле
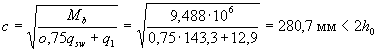
Принимаем co = c = 280,7 мм. Тогда
Qsw = 0,75qswco = 0,75·143,3·280,7 = 30168 Н = 30,17 кН.
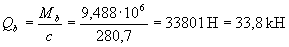
Q = Qmax – q1c = 62 - 12,9·0,28 = 58,4 кН.
Проверяем условие (3.44)
Qb + Qsw = 33,8 + 30,17 = 63,97 Н > Q = 58,4 кН,
т.е. прочность наклонных сечений обеспечена.
Проверим требование п.3.35:
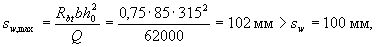
т.е. требование выполнено. Условия п.5.21 sw < hо/2= 315/2 = 157 мм и sw < 300 мм также выполнены.
Пример 13. Дано: свободно опертая балка перекрытия с размерами сечения: b = 200 мм, h = 400 мм; ho = 370 мм; бетон класса В25 (Rbt = 1,05 МПа); хомуты двухветвевые диаметром 8 мм (Asw = 101мм2) с шагом sw= 150 мм; арматура класса А240 (Rsw = 170 МПа); временная эквивалентная по моменту нагрузка qv = 36 кН/м, постоянная нагрузка qg = 14 кН/м; поперечная сила на опоре Qmax = 137,5 кН.
Требуется проверить прочность наклонных сечений.
Расчет. Прочность наклонных сечений проверяем согласно п.3.31. По формуле (3.48) определим интенсивность хомутов
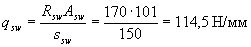
Поскольку 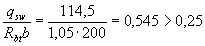 , т.е. условие (3.49) выполняется, хомуты учитываем полностью и значение Мb определяем по формуле (3.46)
, т.е. условие (3.49) выполняется, хомуты учитываем полностью и значение Мb определяем по формуле (3.46)
Мb = 1,5Rbtbhо2= 1,5·1,05·200·3702 = 4,312·107 Н·мм.
Согласно п.3.32 определяем длину проекции невыгоднейшего наклонного сечения:
q1 = qg + 0,5qv = 14 + 0,5·36 = 32 кН/м (Н/мм).
Поскольку
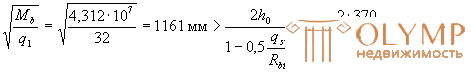
значение с принимаем равным 1161 мм > 2h0 = 740 мм. Тогда сo = 2h0 = 740 мм и Qsw = 0,75qswco = 0,75·114,5·740 = 63548 Н = 63,55 кН;
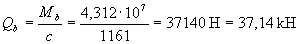
Q = Qmax – q1c = 137,5 - 32·1,161 = 100,35 кН.
Проверяем условие (3.44)
Qb + Qsw = 37,14 + 63,55 = 100,69 кН > Q = 100,35 кН,
т.е. прочность наклонных сечений обеспечена.
Пример 14. Дано: свободно опертая балка перекрытия пролетом l = 5,5 м; полная равномерно распределенная нагрузка на балку q = 50 кН/м; временная эквивалентная нагрузка qv = 36 кН/м; размеры поперечного сечения b = 200 мм, h = 400 мм; ho = 370 мм; бетон класса В15 (Rbt = 0,75 МПа); хомуты из арматуры класса А240 (Rsw =170 МПа).
Требуется определить диаметр и шаг хомутов у опоры, а также выяснить, на каком расстоянии и как может быть увеличен шаг хомутов.
Расчет. Наибольшая поперечная сила в опорном сечении равна
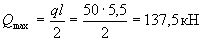
Определим требуемую интенсивность хомутов приопорного участка согласно п.3.33,б.
По формуле (3.46) определяем Мb
Мb = 1,5Rbtbh02= 1,5·0,75·200·3702 = 30,8·106 Н·мм.
Согласно п.3.32
q1 = q - 0,5qvt = 50 - 0,5·36 = 32 кН/м (Н/мм).
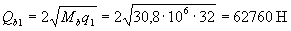
Так как 2Мb/ho - Qmax = 2·30,8·106/370 - 137500 = 28986 Н < Qb1= 62790H, интенсивность хомутов определяем по формуле (3.52)
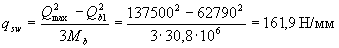
Согласно п.5.21 шаг хомутов sw у опоры должен быть не более ho/2 = 185 и 300 мм, а в пролете - 0,75ho = 271 и 500 мм. Максимально допустимый шаг у опоры согласно п.3.35 равен
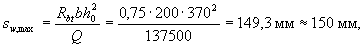
Принимаем шаг хомутов у опоры sw1= 150 мм, а в пролете 250 мм. Отсюда
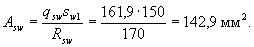
Принимаем в поперечном сечении два хомута по 10 мм (Asw = 157 мм2).
Таким образом, принятая интенсивность хомутов у опоры и в пролете соответственно равны:
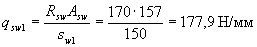
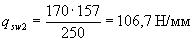
Проверим условие (3.49):
0,25Rbtb = 0,25·0,75·200 = 37,5 Н/мм < qsw1 и 37,5 < qsw2
Следовательно, значения qsw1 и qsw2 не корректируем.
Определим, согласно п.3.34 длину участка l1 с интенсивностью хомутов qsw1. Так как Δ qsw = 0,75(qsw1 - qsw2) = 0,75(177,9 - 106,7) = 53,4 Н/мм > q1 = 32 Н/мм, значение l1 вычислим по формуле (3.59), приняв Qb.min = 0,5Rbtbho= 0,5·55500 = 27750 Н
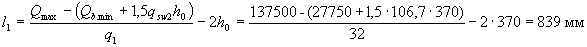
Принимаем длину участка с шагом хомутов sw1 = 150 мм равной 0,9 м.
Пример 15. Дано: балка покрытия, нагруженная сосредоточенными силами как показано на черт.3.22,а; размеры сечения - по черт.3.22,б; бетон класса В15 (Rbt = 0,75 МПа); хомуты из арматуры класса А240 (Rsw = 170 МПа).
Требуется определить диаметр и шаг хомутов, а также выяснить, на каком расстоянии от опоры и как может быть увеличен шаг хомутов.
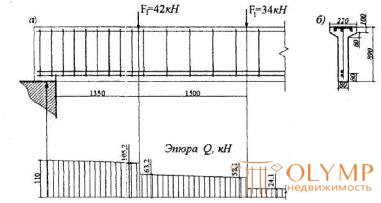
Черт.3.22. К примеру расчета 15
Расчет. ho = 890 - 80 = 810 мм.
Определим требуемую интенсивность хомутов qsw согласно п.3.33,а, принимая длину проекции сечения с, равной расстоянию от опоры до первого груза – c1 = 1350 мм. Тогда a1 = c1/ho = 1350/810 = 1,667 < 2, и, следовательно, a01 = a1 = 1,667.
Определяем 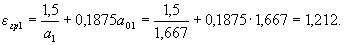
Согласно черт.3.22 поперечная сила на расстоянии с1 от опоры равна Q1 = 105,2 кН. Тогда 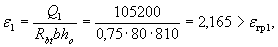 и, следовательно, qsw определяем по формуле (3.51):
и, следовательно, qsw определяем по формуле (3.51):
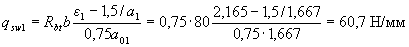
Определим qsw при значении с, равном расстоянию от опоры до второго груза - с2 = 2850 мм:
a2 = c2/ho = 2850/810 = 3,52 > 3; принимаем a2 = 3,0.
Поскольку a2 > 2, принимаем a02 = 2,0.
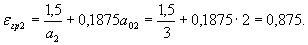
Соответствующая поперечная сила равна Q2 = 58,1 кН. Тогда
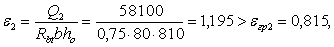
и, следовательно,
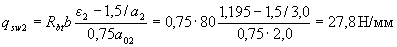
Принимаем максимальное значение qsw = qsw1 = 60,7. Из условия сварки принимаем диаметр хомутов 8 мм (Asw = 50,3 мм2). Тогда максимально допустимый шаг хомутов на приопорном участке равен
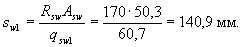
Принимаем sw1 =100 мм. Назначаем шаг хомутов в пролете равным sw2 = 300 мм. Тогда интенсивность хомутов приопорного участка
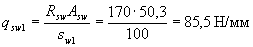
а пролетного участка
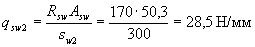
Зададим длину участка с шагом хомутов sw1, равной расстоянию от опоры до первого груза – l1 = 1350 мм, и проверим условие (3.44) при значении с, равном расстоянию от опоры до второго груза - с = 2850 мм. Но поскольку 3ho = 3·810 = 2430 мм < с, принимаем с = 2430мм. Значение Qsw определяем согласно п.3.34.
Так как 2ho + l1 = 2·810 + 1350 = 2970 мм > с, значение Qsw определяем по формуле (3.56). При этом, поскольку с > 2ho, со = 2ho = 1620 мм.
Qsw = 0,75[qsw1co - (qsw1 - qsw2)(c - l1)] = 0,75[85,5·1620 - (85,5 -28,5)(2430 -1350)] =
57712 Н = 57,7 кН.
При с =3ho, Qb = Qb.min = 0,5Rbtbhо = 0,53·0,75·80·810 = 24300 H = 24,3 кН.
Поперечная сила на расстоянии с = 2430 мм от опоры (черт.3.22) равна
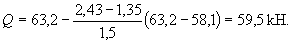
Проверяем условие (3.44)
Qb + Qsw = 24,3 + 57,7 = 82,0 кН > Q = 59,5 кН,
т.е. прочность этого наклонного сечения обеспечена.
Большее значение с не рассматриваем, поскольку при этом поперечная сила резко уменьшается.
Таким образом, длину участка с шагом хомутов swl = 100 мм принимаем равной 1,35 м.
Пример 16. Дано: двухскатная балка пролетом 8,8 м (черт.3.23,а); сплошная равномерно распределенная нагрузка на балку q = 46 кН/м; размеры опорного сечения по черт.3.23,б; бетон класса В20 (Rbt = 0,9 МПа); хомуты из арматуры класса А400 (Rsw = 285 МПа) диаметром 10 мм (Asw = 78,5 мм2) шагом sw = 100 мм.
Требуется проверить прочность наклонного сечения по поперечной силе.
Расчет. Рабочая высота опорного сечения равна ho = 600 - 40 = 560 мм (см. черт.3.23,б). По формуле (3.48) определим интенсивность хомутов
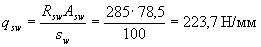
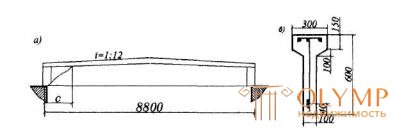
Черт.3.23. К примеру расчета 16
Определим проекцию невыгоднейшего наклонного сечения с согласно п.3.37. Из черт.3.23,а имеем tgβ= 1/12, b = 100 мм,
Rbt b = 0,9·100 = 90 Н/мм; 1 - 2tgβ = 1 - 2 / 12 = 0,833.
Поскольку qsw /(Rbtb) = 223,7/90 = 2,485 > 2(1 - 2tgβ)2 = 2·0,8332 = 1,389, значение с вычисляем по формуле (3.62).
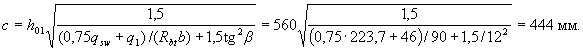
Рабочая высота поперечного сечения ho на расстоянии с = 444 мм от опоры равна
ho = ho1 + с·tgβ = 560 + 444/12 = 597 мм.
Поскольку с = 444 мм < 2ho, сo = с = 444 мм;
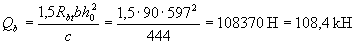
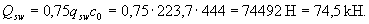
Проверим условие (3.44), принимая поперечную силу в конце наклонного сечения равной
Q = Qmax – q1c=(46·8,8)/2 - 46·0,444 = 182,0 кН:
Qb + Qsw = 108,4 + 74,5 = 182,9 кН > Q = 182 кН,
т.е. прочность наклонных сечений по поперечной силе
обеспечена.
Пример 17. Дано: консоль размерами по черт.3.24, сосредоточенная сила на консоли F = 130 кН, расположенная на расстоянии l1 = 0,8 м от опоры; бетон класса В15 (Rbt = 0,75 МПа); хомуты двухветвевые диаметром 8 мм (Asw= 101 мм2) из арматуры класса А240 (Rsw = 170 МПа) шагом sw = 200 мм.
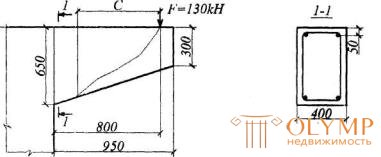
Черт.3.24. К примеру расчет 17
Требуется проверить прочность наклонных сечений по поперечной силе.
Расчет. Согласно п.3.38 проверяем из условия (3.44) невыгоднейшее наклонное сечение, начинающееся от места приложения сосредоточенной силы, при значении с, определенном по формуле (3.62) при q1 = 0 и 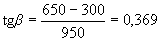 .
.
Рабочая высота в месте приложения сосредоточенной силы равна  (см. черт.3.24); Rbtb = 0,75·200 = 150Н/мм.
(см. черт.3.24); Rbtb = 0,75·200 = 150Н/мм.
Значение qswравно
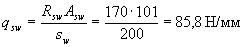
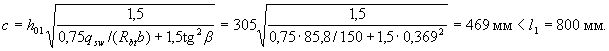
Поскольку 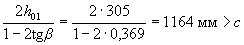 , оставляем с = 469,4 мм.
, оставляем с = 469,4 мм.
Определим рабочую высоту ho в конце наклонного сечения
h0= h0l + с·tgβ = 305 + 469·0,369 = 478 мм.
Поскольку с = 469,4 > 2ho, сo = с = 469 мм.
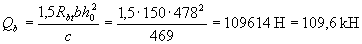
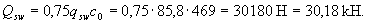 ;
;
Qb + Qsw = 109,6 + 30,2 = 139,8 кН > F = 130 кН,
т.е. прочность наклонных сечений по поперечной силе обеспечена.
Пример 18. Дано: сплошная плита днища резервуара без поперечной арматуры размером 3x6 м толщиной h = 160 мм, монолитно связанная по периметру с балками; полная равномерно распределенная нагрузка 50 кН/м2; бетон класса В15 (Rbt = 0,75 МПа).
Требуется проверить прочность плиты на действие поперечной силы.
Расчет. ho = 160 - 20 = 140 мм. Расчет проводим для полосы шириной b = 1,0 м = 1000 мм, пролетом l = 3 м. Тогда q = 50·1,0 = 50 кН/м, а поперечная сила на опоре равна
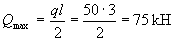
Проверим условие (3.64)
2,5Rbtbh0 = 2,5·0,75·1000·140 = 262500 Н > Qmax = 75 кН.
Проверим условие (3.66), принимая q1 = q - 50 кН/м (Н/мм). Поскольку боковые края плиты монолитно связаны с балками, условие (3.66) имеет вид
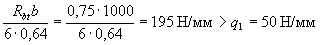
следовательно, прочность плиты проверяем из условия (3.67а)
0,625Rbtbhо + 2hоq1 = 0,625·0,75·1000·140 + 2,4·140·50 = 82425 Н =
82,4 кН > Qmax = 75 кН,
т.е. прочность плиты по поперечной силе обеспечена.
Пример 19. Дано: панель стенки резервуара консольного типа с переменной толщиной от 262 (в заделке) до 120 мм (на свободном конце) вылетом 4,25 м; боковое давление грунта, учитывающее нагрузку от транспортных средств на поверхности грунта, линейно убывает от qo = 55 кН/м2 в заделке до q = 6 кН/м2 на свободном конце; а = 22 мм; бетон класса В15 (Rbt = 0,75 МПа).
Требуется проверить прочность панели на действие поперечной силы.
Расчет. Рабочая высота сечения панели в заделке равна ho1 = 262-22 = 240 мм.
Определим tgβ (β - угол между растянутой и сжатой гранями):
tgβ =(262-120)/4250 = 0,0334.
Проверим условия п.3.41. Поперечная сила в заделке равна
Qmax =((55+6)/2)·4,25 = 129,6 кН.
Расчет производим для полосы панели шириной b = 1,0 м = 1000 мм.
Проверим условие (3.64), принимая ho = ho1 = 240 мм.
2,5Rbtbhо= 2,5·0,75·1000·240 = 450000 Н = 450 кН > Qmax
т.е. условие выполняется.
Поскольку панели связаны друг с другом, а ширина стенки резервуара заведомо больше 5h, значение cmaxопределяем по формуле
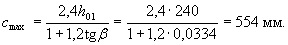
Средняя интенсивность нагрузки на приопорном участке длиной cmax = 554 мм равна
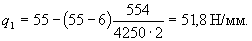
Поскольку
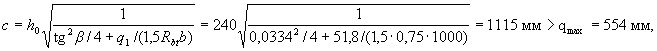
принимаем с = cmax = 554 мм.
Определим рабочую высоту сечения на расстоянии с/2 от опоры (т.е. среднее значение ho в пределах длины с):
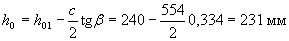 .
.
Поперечная сила на расстоянии с = 554 мм от опоры равна:
Q = Qmax – q1c= 129,6 - 51,8·0,554 = 100,9 кН.
Проверим условие (3.65):
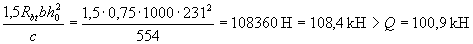
т.е. прочность панели по поперечной силе обеспечена.
Расчет наклонных сечений на действие момента
Пример 20. Дано: свободно опертая балка пролетом l = 5,5м с равномерно распределенной нагрузкой q = 29 кН/м; конструкция приопорного участка балки принята по черт.3.25; бетон класса В15 (Rb = 8,5 МПа); продольная арматура без анкеров класса А400 (Rs =355 МПа) площадью сечения As = 982 мм2 (2Æ25); хомуты из арматуры класса А240 (Rsw =170 МПа) диаметром 8 мм шагом sw =150 мм приварены к продольным стержням.
Требуется проверить прочность наклонных сечений на действие момента.
Расчет. ho = h - а = 400 - 40 = 360 мм. Поскольку растянутая арматура не имеет анкеров, расчет наклонных сечений на действие момента необходим.
Определим усилие в растянутой арматуре по формуле (3.73).
Принимаем начало наклонного сечения у грани опоры. Отсюда ls = lsup - 10 мм = 280 - 10 = 270 мм (см. черт.3.25).
Опорная реакция балки равна
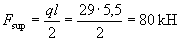
а площадь опирания балки Asup = blsup = 200·280 = 56000 мм2,
откуда 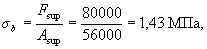
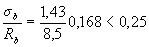 ,
,
следовательно, а = 1,0. Из табл.3.3 при классе бетона В15, классе арматуры А400 и а = 1,0 находим λan = 47. Тогда, длина анкеровки равна lan = λands = 47·25 = 1175 мм.
Ns= RsAs(ls/lan) = 355·982·(270/1175) = 80106 Н.
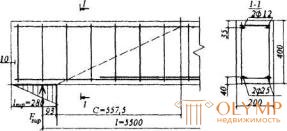
Черт.3.25. К примеру расчета 20
Поскольку к растянутым стержням в пределах длины ls приварены 4 вертикальных и 2 горизонтальных поперечных стержня (см. черт.3.25), увеличим усилия Ns на величину Nw.
Принимая dw = 8 мм, nw = 6, φw = 150 (см. табл.3.4), получаем
Nw = 0,7nw φw dw2Rbt = 0,7·6·1502·0,75 = 30,24·103 Н.
Отсюда Ns = 80106 + 30240 = 110346 Н.
Определяем максимально допустимое значение Ns. Из табл.3.3 при а = 0,7 находим λan = 33; тогда 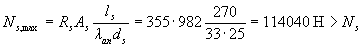 , т.е. оставляем Ns = 110346 Н. Определим плечо внутренней пары сил
, т.е. оставляем Ns = 110346 Н. Определим плечо внутренней пары сил
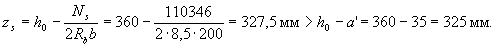
Тогда момент, воспринимаемый продольной арматурой, равен
Ms= Nszs= 110346·327,5 = 36,1·106Нмм.
По формуле (3.48) вычислим величину qsw
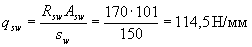
Определяем длину проекции невыгоднейшего наклонного сечения по формуле (3.76), принимая значение Qmaxравным опорной реакции балки, т.е. Qmax = Fsup = 80 кН.
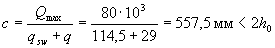
Тогда момент, воспринимаемый поперечной арматуры, равен
Msw =0,5qswc2 = 0,5·114,5·557,52 = 17,8·106 Н мм.
Момент в наклонном сечении определяем как момент в нормальном сечении, расположенном в конце наклонного сечения, т.е. на расстоянии от точки приложения опорной реакции, равной x = lsup/3 + с = 280/3 + 557,5 = 650,8 мм
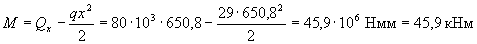 .
.
Проверяем условие (3.69)
Ms + Мsw = 36,1 + 17,8 = 53,9 кНм >М = 45,9 кНм,
т.е. прочность наклонных сечений по изгибающему моменту обеспечена.
Пример 21. Дано: ригель многоэтажной рамы с эпюрами моментов и поперечных сил от равномерно распределенной нагрузки q = 228 кН/м по черт.3.26; бетон класса В25; продольная и поперечная арматура класса А400 (Rs = 355 МПа, Rsw = 285 МПа); поперечное сечение приопорного участка - по черт.3.26; хомуты трехветвевые диаметром 10 мм (Rsw = 236 мм2) шагом sw равным 150 мм.
Требуется определить расстояние от левой опоры до места обрыва первого стержня верхней арматуры.
Расчет. Из черт.3.26 имеем: ho = h - a = 800 - 60 = 740 мм; а -50 мм; площадь сечения верхней растянутой арматуры без учета одного обрываемого стержня Æ32 As = 1609 мм2 (2Æ32); As = 2413 мм2 (3Æ32). Определим предельный момент, соответствующий этой арматуре по формуле (3.19), поскольку As < A's, т.е. х < 0:
Mult = RsAs(ho – а') = 355·1609·(740 - 50) = 394,1·106Н мм = 394,1 кНм.
По эпюре моментов определяем расстояние от опоры до места теоретического обрыва первого стержня из уравнения
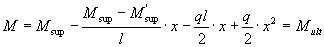
откуда 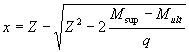 , где
, где 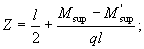
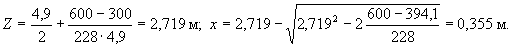
Поперечная сила в месте теоретического обрыва равна
Q = Qmax - q·x = 620 - 228·0,355 = 539 кН.
Определим величину qsw,
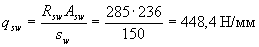
Поскольку 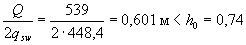 м, длину w, на которую надо завести обрываемый стержень за точку теоретического обрыва, определяем по формуле (3.79)
м, длину w, на которую надо завести обрываемый стержень за точку теоретического обрыва, определяем по формуле (3.79)
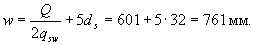 .
.
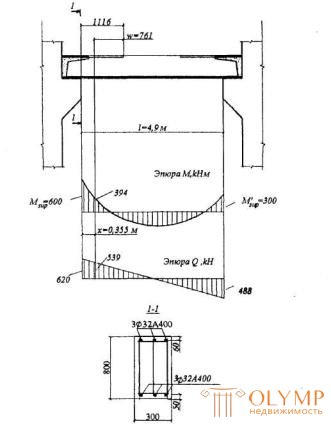
Черт.3.26. К примеру расчета 21
Следовательно, расстояние от опоры до места обрыва стержня может быть принято равным х + w = 355 + 761 = 1116 мм.
Определим необходимое расстояние lan от места обрыва стержня до опорного сечения, предполагая полное использование этого стержня в опорном сечении. Для этого по табл.3.3 при а = 1,0 классе бетона В25, классе арматуры А400 находим λ = 34. Тогда lan = λand = 34·32 = 1088 мм < 1116 мм.
Следовательно, обрываем стержень на расстоянии 1116 мм от опоры.
Что бы оставить комментарий войдите
Комментарии (0)