Расчеты на прочность При прямом поперечном изгибе кратко

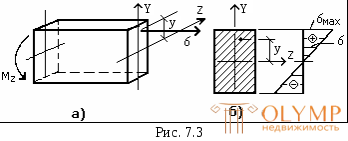
При прямом поперечном изгибе в поперечном сечении бруса действуют нормальные и касательныенапряжения.

Нормальные напряжения вызваны изгибающим моментом и определяются по формуле:

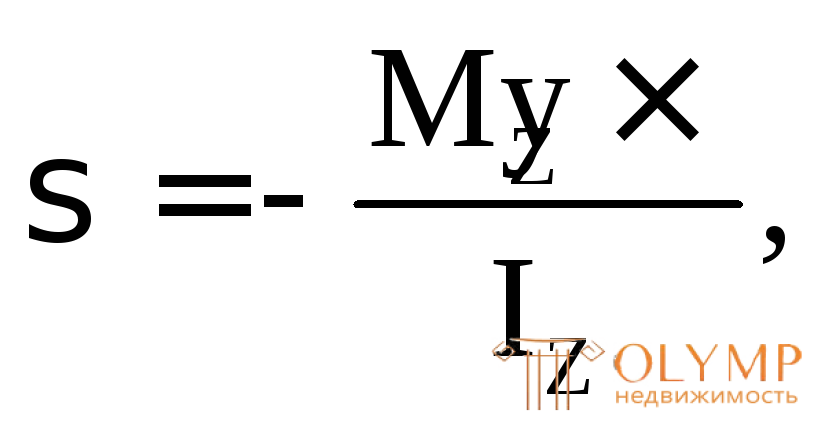(7.3)

где – величина изгибающего момента в сечении; у – ордината точки, где определяется(рис. 7.3); 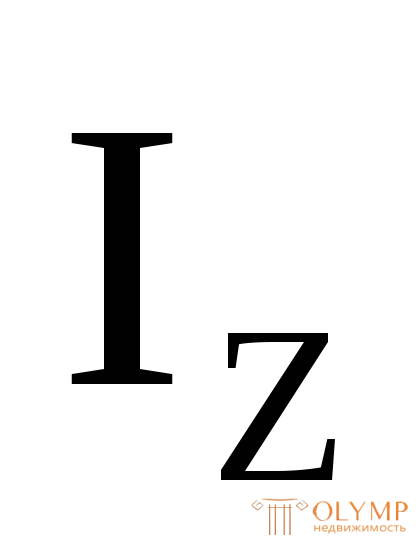– главный центральный момент инерции сечения бруса.

По формуле (7.3) можно определять нормальные напряжения в любой точке, лежащей на горизонтальной линии поперечного сечения бруса и отстоящей от нейтральной оси Z на расстоянии у. Знак "минус" перед формулой (7.3) поставлен для того, чтобы при принятых правилах знаков для изгибающих моментов знак полученного нормального напряжения соответствовал характеру деформации точек сечения: "плюс" – растяжению, "минус" – сжатию.

Из соотношения (7.3) видно, что нормальное напряжение зависит от величины у линейно. График, изображающий закон изменения нормальных напряжений по высоте сечения, называемый эпюрой напряжений, показан на рис. 7.3б. Наибольшее нормальное напряжение будет в точке, для которой величина у в формуле (7.3) принимает максимальное значение, т.е. в наиболее удаленной от нейтральной оси точке сечения.

При прямом изгибе нейтральная ось совпадает с главной центральной осью поперечного сечения, перпендикулярной плоскости действия сил.

Анализ формулы (7.3) для определения нормальных напряжений при прямом изгибе и их эпюра (рис. 7.3б) позволяют записать условия прочности при прямом изгибе по нормальным напряжениям. Для пластичных материалов (при R_t = R_c = R) это условие имеет вид:

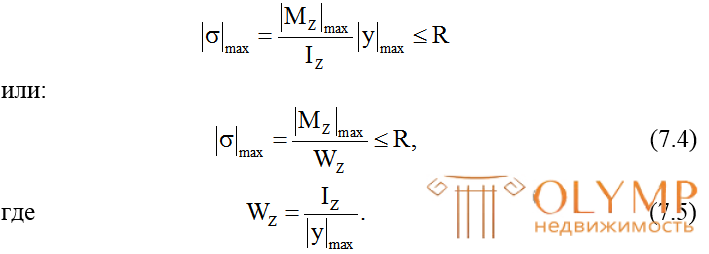
Здесь 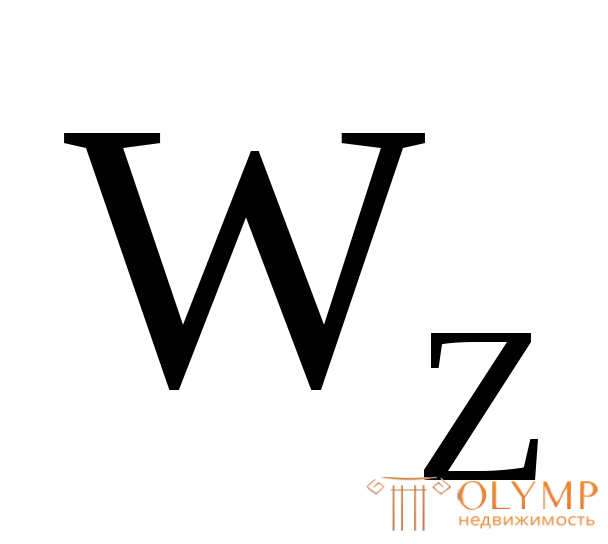называетсяосевым моментом сопротивления сечения; 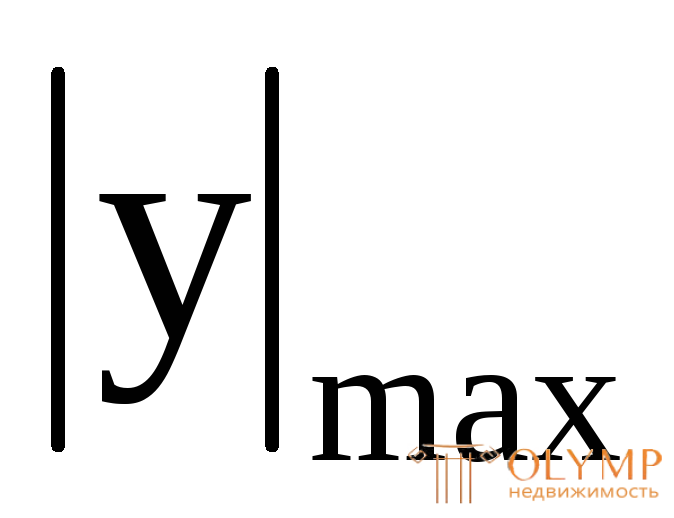– расстояние от нейтральной (центральной) оси до наиболее удаленной точки сечения, взятое по модулю;R – расчетное сопротивление материала по пределу текучести.

Для хрупких материалов, когда расчетные сопротивления материала на растяжение (R_t) и на сжатие (R_c) не равны между собой, т.е. R_t R_c, условия прочности для растянутой и сжатой зон записываются отдельно:

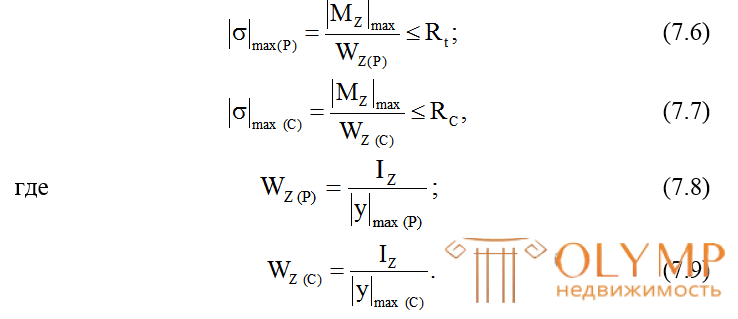
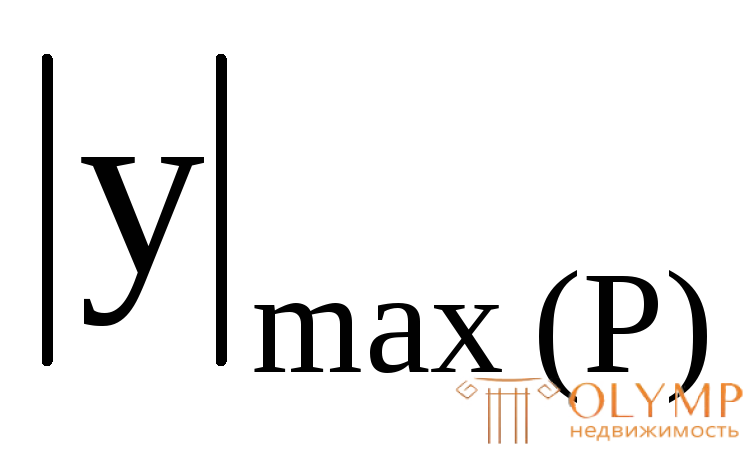В формулах (7.8) и (7.9) величины и 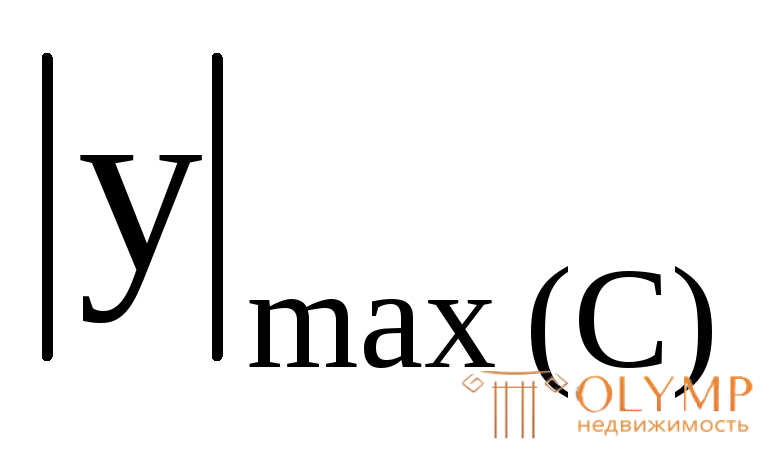означают наибольшие по модулю расстояния от нейтральной оси сечения соответственно до наиболее растянутого и сжатого волокна. В таких случаях в первую очередь с помощью эпюры изгибающих моментов нужно выяснить, какая часть сечения работает на растяжение, какая – на сжатие.

В приведенных условиях прочности при прямом изгибе 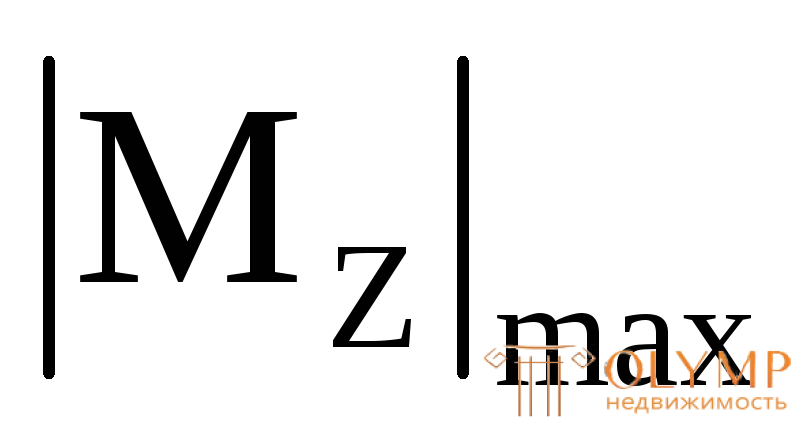означает наибольшее по модулю значение изгибающего момента и берется из эпюры М.

Как и для других видов деформации, условия прочности при прямом изгибе (7.4), (7.6) и (7.7) позволяют решать три типа задач:

1. Проверочная задача – проверка прочности при всех известных данных непосредственно с помощью приведенных формул.

2. Проектная задача – подбор сечения балки. Для решения задач этого типа из условия прочности определяют требуемое значение осевого момента сопротивления, принимая условие прочности со знаком равенства, т.е. 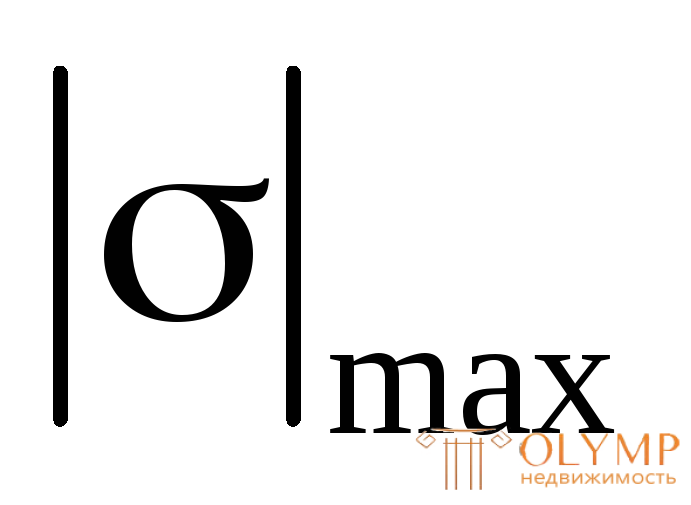=R.

Например, для балки из пластичного материала из формулы (7.4) получаем

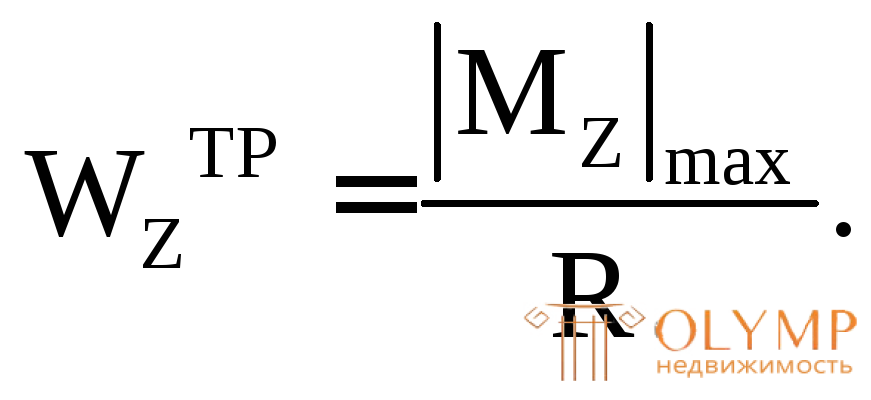
Выражая фактическую величину 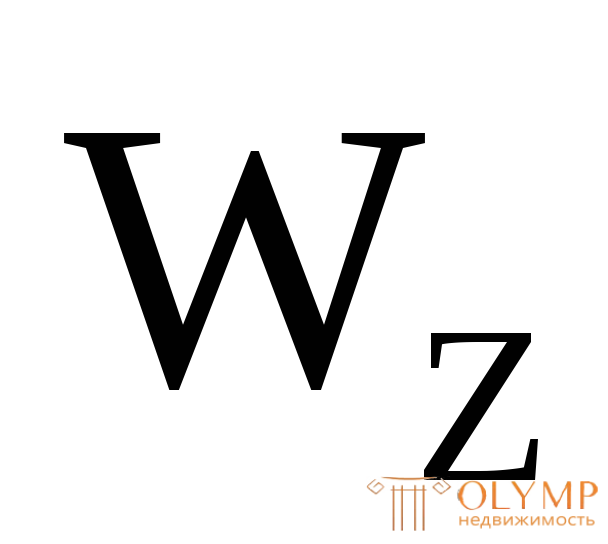через формулу (7.5) из равенства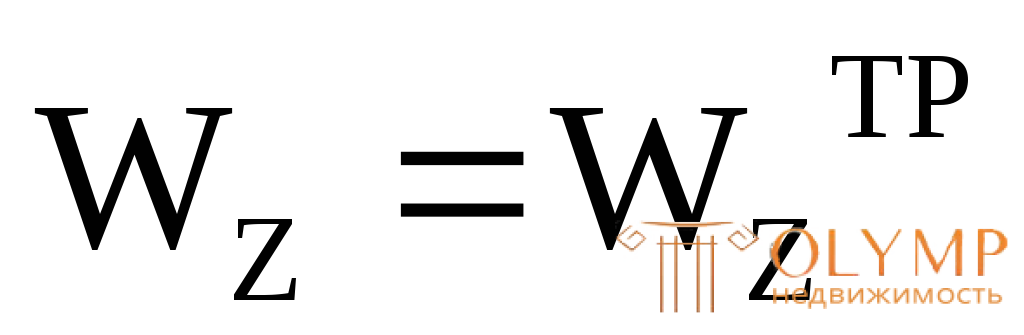, находим неизвестный размер сечения или номер профиля для прокатного элемента из таблицы сортаментов.

3. Определение допускаемого значения изгибающего момента, т.е. определение несущей способности балки с заданными размерами и характеристиками:

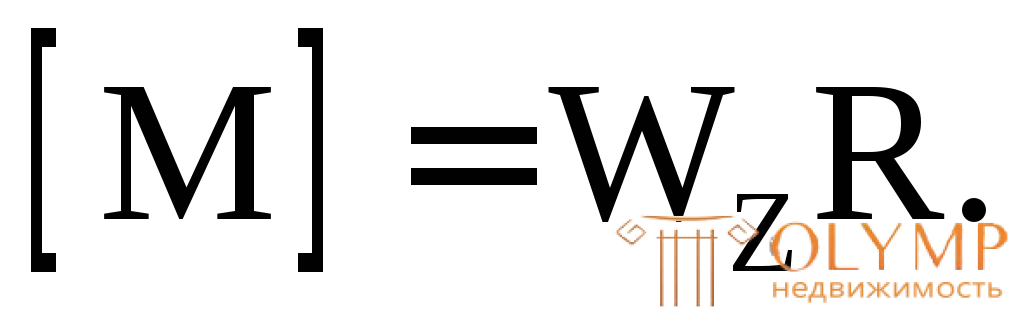
Касательные напряжения в сечении при прямом поперечном изгибе возникают от поперечной силы и определяются по формуле Д.И. Журавского:

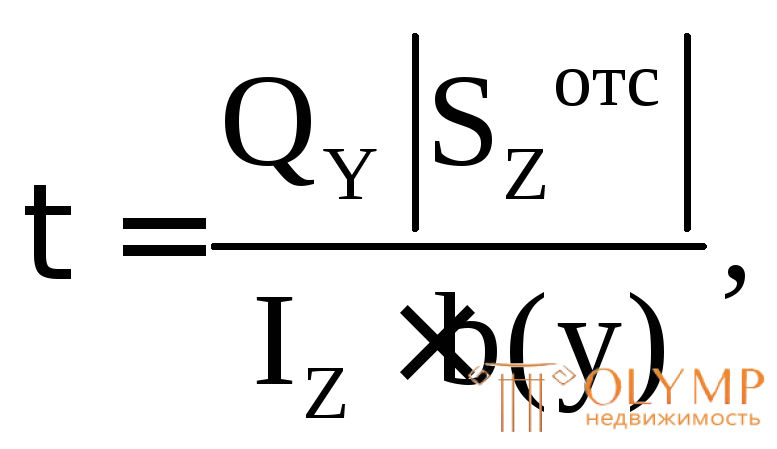(7.10)

где Q_Y – поперечная сила в том сечении, в точках которого определяются касательные напряжения; 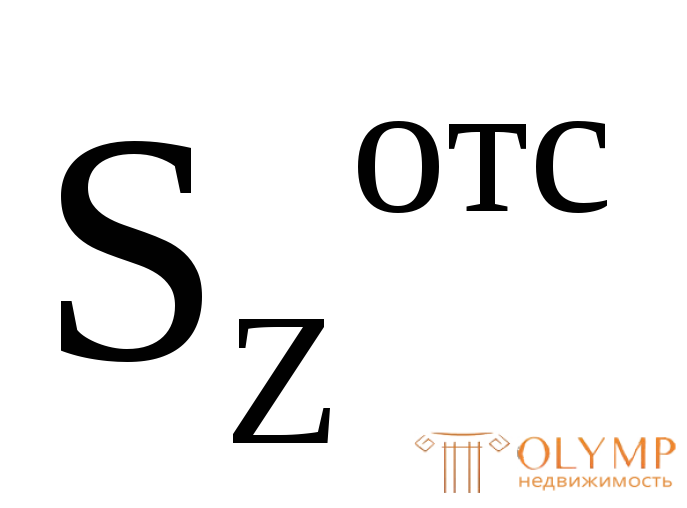– статический момент отсеченной части площади поперечного сечения (части площади выше или ниже точки, в которой определяются касательные напряжения) относительно центральной (нейтральной) осиZ, взятый по абсолютной величине; b(y) – ширина сечения на уровне точки, для которой определяется касательное напряжение (на расстоянии у от нейтральной оси).

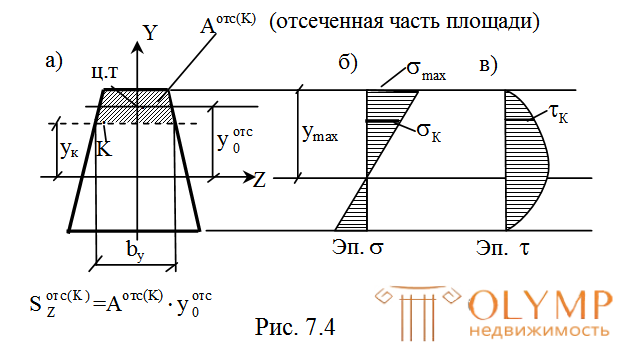
Определение b(y) и 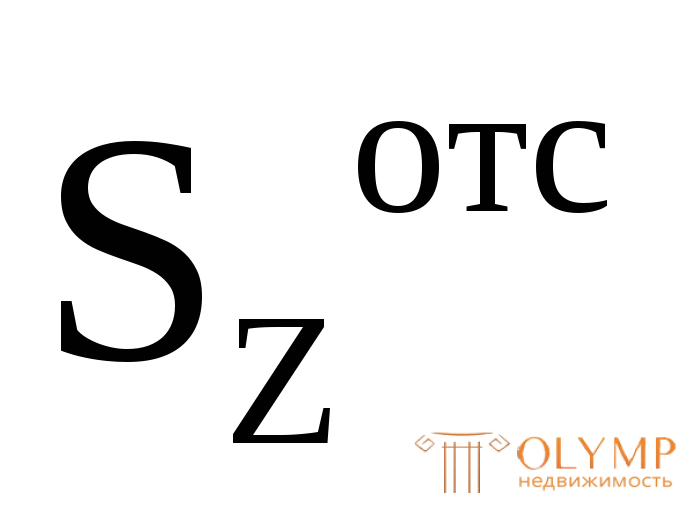для произвольной точки произвольного сечения, а так же характер распределения нормальных и касательных напряжений покажем на примере сечения в виде трапеции (рис. 7.4).

Наибольшие по модулю касательные напряжения 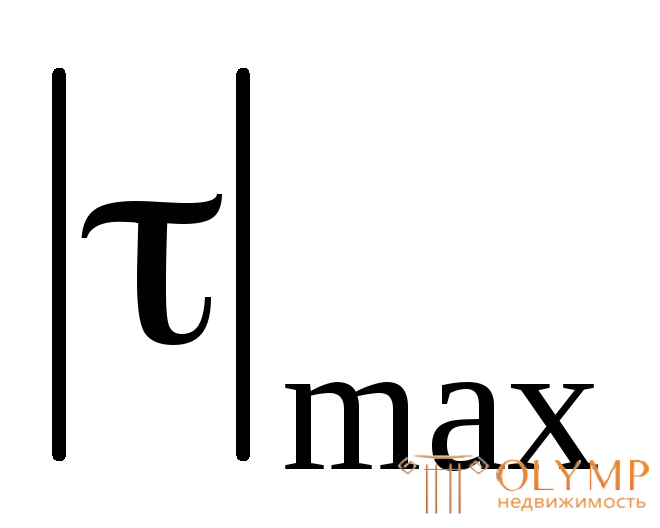будут в тех точках, где отношение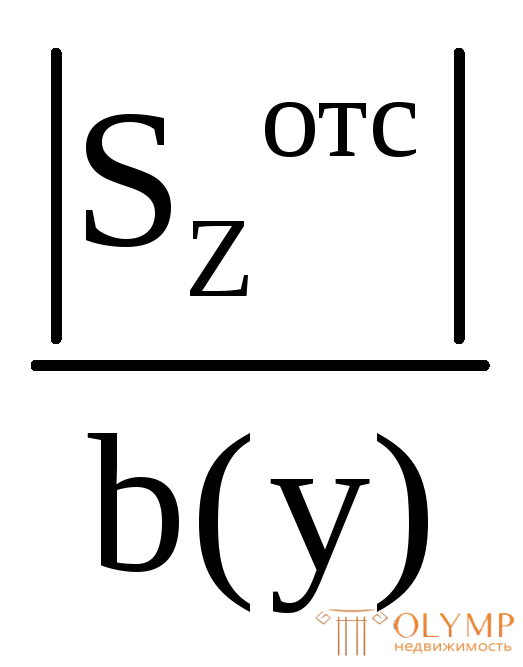достигает максимума. В частности, для прямоугольного сечения принаибольшие по модулю касательные напряжения возникают в точках нейтральной оси, так как статический момент полусечения относительно центральной оси всегда больше, чем для других частей сечения.

В общем случае, условие прочности балки по касательным напряжениям будет иметь вид:

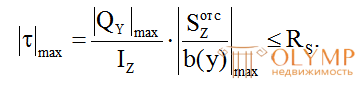(7.11)

Здесь R_S – расчетное сопротивление материала на сдвиг.

Наибольшие по модулю значения изгибающего момента 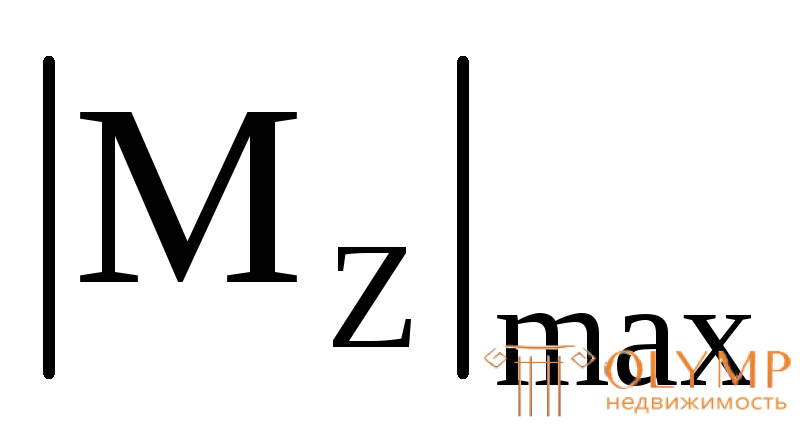и поперечной силы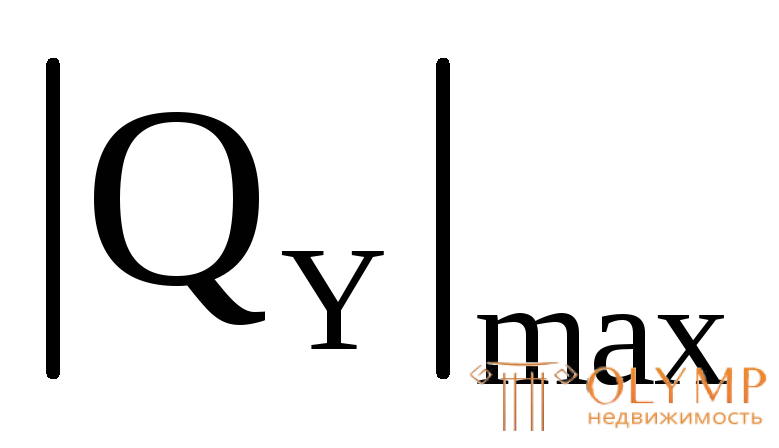, берут из соответствующих эпюр.

Принимая во внимание, что при прямом изгибе другие внутренние силовые факторы, кроме иQ_Y, равны нулю, в дальнейшем при их обозначении нижние индексы Z и Y будем опускать.