Теории прочности кратко

При испытании материалов статической нагрузкой на центральное растяжение и сжатие устанавливается их так называемое, опасное (или предельное) состояние. Оно характеризуется наступлением текучести материала, сопровождаемое значительными остаточными деформациями или появлением трещин, свидетельствующих о начале разрушения. Нормальные напряжения в поперечных сечениях стержней из пластичного материала в момент наступления опасного состояния равны пределу текучести σ_S, а из хрупкого – пределу прочности на растяжение_ut.

Известно, что при расчете элементов конструкций должно быть выполнено условие прочности, требующее, чтобы наибольшее напряжение в каждой точке не превышало величины расчетного сопротивления, составляющего некоторую долю опасного напряжения. Для назначения расчетного сопротивления необходимо изучить поведение материала при его деформировании от начала нагружения до момента разрушения.

Экспериментальное изучение поведения материалов под нагрузкой при линейном напряжении или сжатии на существующих лабораторных установках не встречает затруднений. Полученные в результате экспериментов диаграммы растяжения или сжатия дают наглядное представление о сопротивлении материала упругому и пластическому деформированию и позволяют определить такие важные для оценки прочности и назначения расчетных сопротивлений механические характеристики, как предел текучести или предел прочности.

При сложном напряженном состоянии, характеризующемся в общем случае тремя различными главными напряжениями, нахождение опасных значений этих напряжений существенно усложняется. Как показывают опыты, опасное напряженное состояние элемента конструкции (текучесть, разрушение) зависит от вида напряженного состояния, т.е. от соотношения между тремя главными напряжениями. Так как число различных возможных соотношений между ними неограниченно велико, то и соответствующих опасных состояний элемента конструкции тоже может быть неограниченно много.

Таким образом, для каждого нового соотношения между главными напряжениями необходимо заново экспериментально устанавливать величину предельных напряжений. Следует иметь в виду, что опыты при сложном напряженном состоянии осуществить гораздо труднее, чем при простом растяжении или сжатии. Они, как правило, требуют изготовления специальных дополнительных приспособлений и установок к имеющимся в лабораториях машинам, более трудоемкие и дорогостоящие.

Поэтому необходимо найти способ составления условия прочности при сложномнапряженном состоянии, пользуясь величинами σ_Sи σ_ut, полученными при опытах длялинейного(одноосного) напряженного состояния.

Поставленная задача может быть решена лишь на основании предположения (гипотезы) о том, каков вид функции, связывающей прочность материала с величиной и знаком главных напряжений, каким фактором вызывается наступление опасного состояния.

Существует несколько таких гипотез, называемых теориями прочности.

1-я теория прочности– теория наибольших нормальных напряжений. Согласно этой теории,опасное состояние наступает тогда, когда наибольшее нормальное напряжение достигает опасного значения для данного материала, т.е.

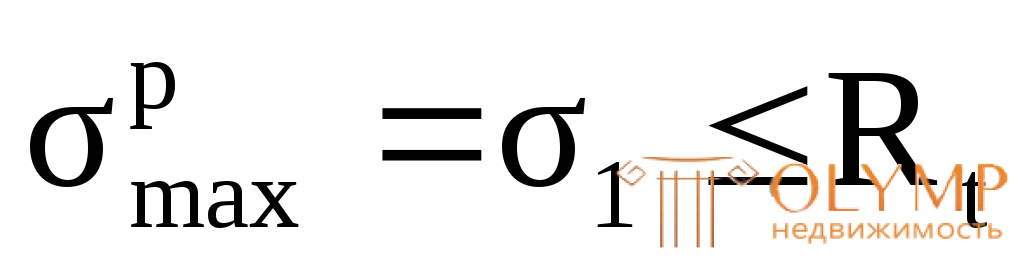или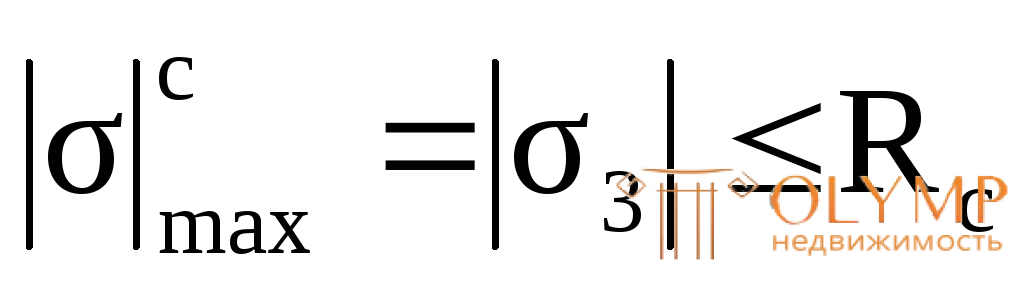, (4.34)

где R_tиR_с– расчетные сопротивления материала на растяжение и сжатие.

Для случаев плоского и объемного напряженного состояний данная теория экспериментально не подтверждается и имеет историческое значение.

2-я теория прочности – теория наибольших относительных удлинений. Согласно этой теории,опасное состояние наступает тогда, когда наибольшие относительные удлинения достигают опасного значения для данного материала.

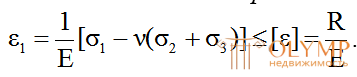. (4.35)

Если в равенствах (4.35) левую и правую части умножим на Е, то получим:

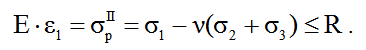. (4.36)

Преимуществом данной теории является то, что она учитывает все три главных напряжения и экспериментально подтверждается для хрупких материалов.

Недостаток данной теории – она не подтверждается экспериментально для пластичных материалов.

3-я теория прочности – теория наибольших касательных напряжений. Согласно этой теории,опасное состояние наступает тогда, когда наибольшие касательные напряжения в данной точке достигают опасного значения для данного материала, т.е. разрушение материала происходит в результате среза.

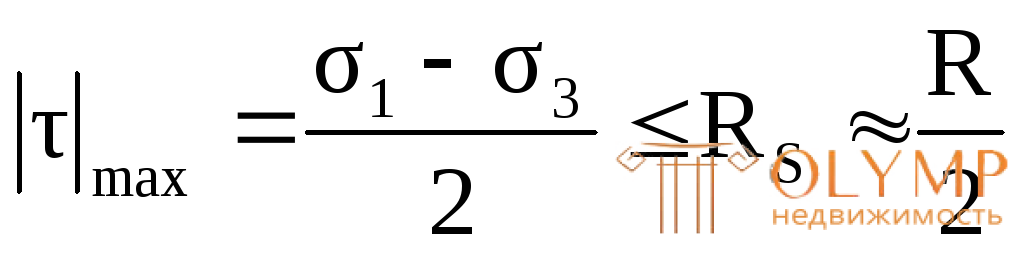. (4.37)

Если в равенствах (4.37) левую и правую части умножить на 2, то получим следующее условие прочности по 3-й теории прочности:

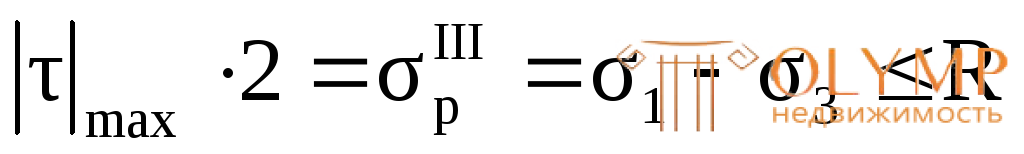. (4.38)

Преимущество данной теории – экспериментально подтверждается для пластичных материалов.

Недостатком теории наибольших касательных напряжений является то, что она не учитывает влияния промежуточного главного напряжения σ₂, а также то, что не объясняет причины разрушения материала при всестороннем равномерном растяжении. Для хрупких материалов эта теория неприменима.

4-я теория прочности – энергетическая. Согласно этой теории,опасное состояние наступает тогда, когда удельная потенциальная энергия изменения формы достигает опасного значения 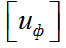для данного материала, определяемого опытным путем для одноосного напряженного состояния. Она широко применяется для пластичных материалов, для хрупких материалов неприменима.

Условие прочности по 4-й теории прочности запишется в следующем виде: 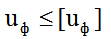или используя (4.33) для u_ф

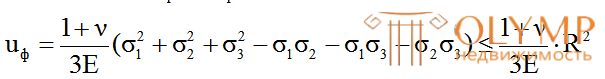(4.39)

откуда, после преобразования, имеем:

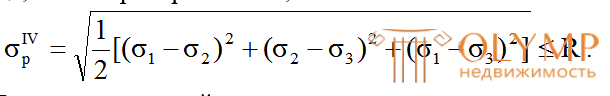. (4.40)

Достоинством этой теории является то, что она учитывает все три главные напряжения. Она, как и 3-я теория, объясняетвысокуюпрочностьматериалапри всестороннем равномерном сжатии,но не объясняетпричиныразрушенияматериала при всестороннем равномерном растяжении.

ПРИМЕР 4.1

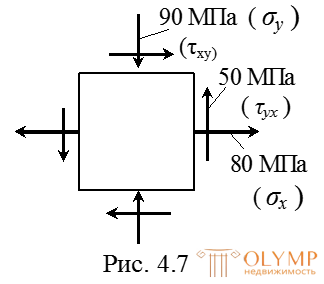
Даны напряжения на двух взаимно перпендикулярных площадках в окрестности некоторой точки (рис. 4.7).

Е = 2,06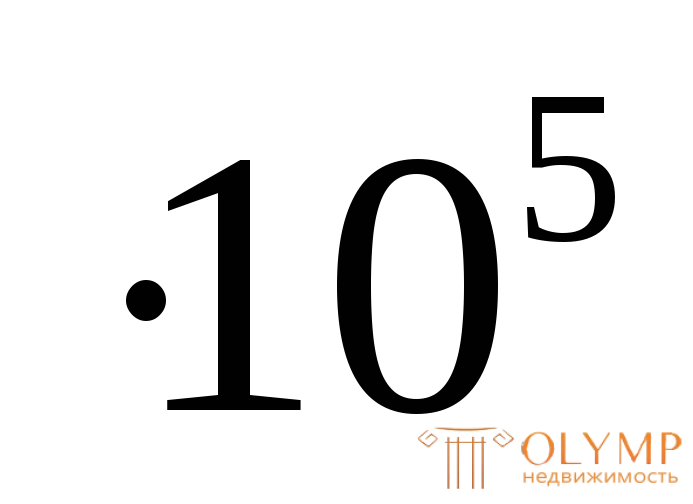МПа,= 0,28.

Требуется исследовать напряженно-деформированное состояние в данной точке.

1. Поставить знаки заданных напряжений в соответствии с их направлениями на рис. 4.7 согласно принятых правил знаков для напряжений.

2. Определить величины и направления главных напряжений, изобразить главные площадки на рисунке и показать на них главные напряжения

3. Вычислить максимальные и минимальные касательные напряжения, изобразить на рисунке площадки, на которых они действуют и показать направления напряжений. Вычислить и показать на чертеже действующие на этих площадках нормальные напряжения.

4. Определить нормальные и касательные напряжения на площадках, повернутых относительно заданных на угол = 30, показать эти площадки и напряжения на них. Определить полное напряжение на этой площадке и относительную деформацию по направлению σ_α .

5. Определить расчетные напряжения с использованием (14)-йтеорий прочности и сравнить их между собой, проанализировать применимость теорий прочности для конкретного материала.

6. Определить относительные деформации по направлениям главных напряжений (главные деформации).

РЕШЕНИЕ

1. Постановка знаков заданных нормальных и касательных напряжений:

σ_х= 80 МПа, ("плюс" – растяжение),

σ_у= –90 МПа ("минус" – сжатие),

σ_ух= –50 МПа ("минус" – против хода часовой стрелки).

2. Вычисление главных напряжений.

==

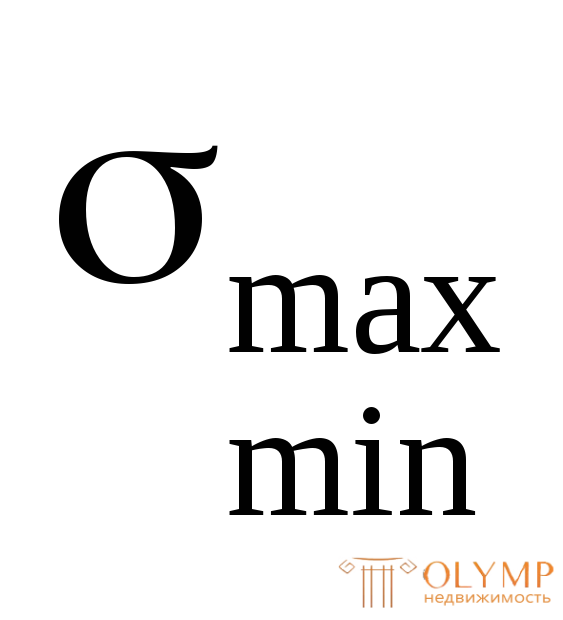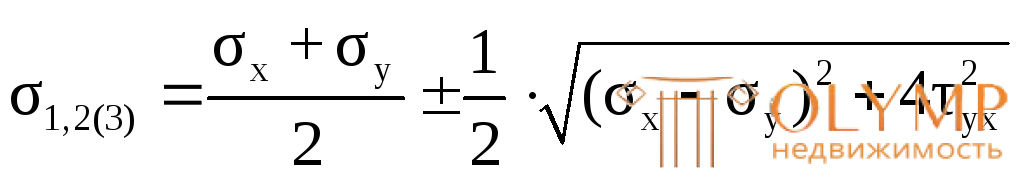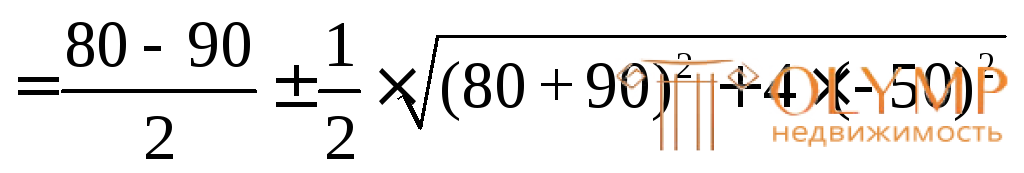= – 598,62.

Соблюдая условие σ₁≥ σ₂≥ σ₃, выпишем числовые значения главных напряжений:

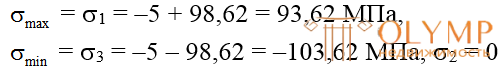(по условию задачи).

Проверка: 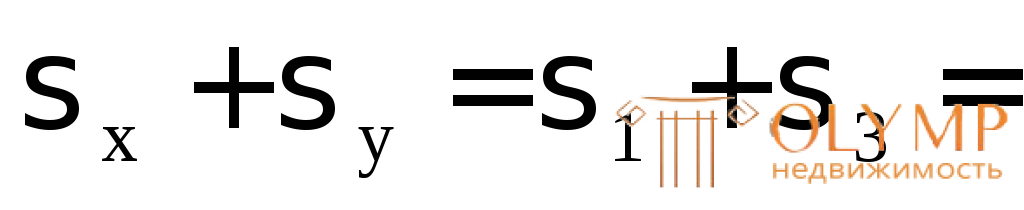80 – 90 = 93,62 – 103,62 = –10 МПа.

Определяем угол наклона главных площадок к заданным:

;

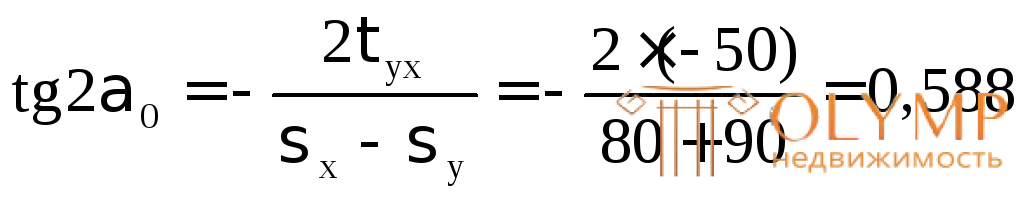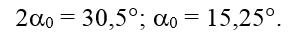
Угол положительный, поэтому заданные площадки должны быть повернутыпротив хода часовой стрелкии на полученных главных площадках показываем главные напряжения.

При этом максимальным напряжением будет то напряжение, которое проходит в четвертях, где сходятся стрелки касательных напряжений и оно будет находиться ближе напряжению _х, которое алгебраически больше, чем _у (рис. 4.8).

3. Определение максимального и минимального касательных напряжений на площадках сдвига по формуле (4.12):

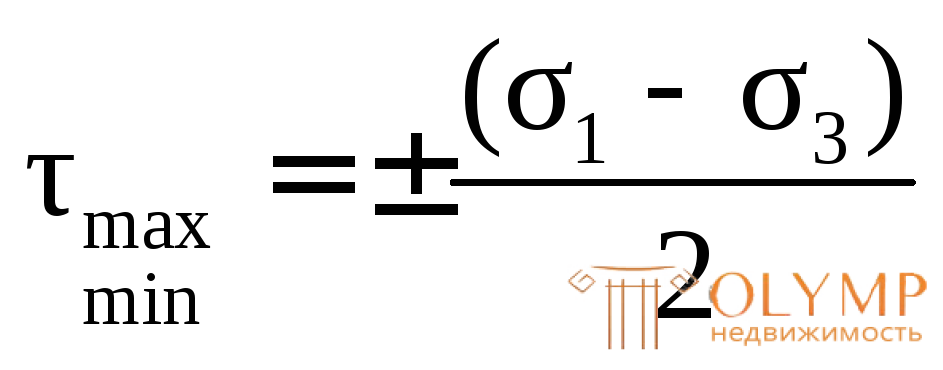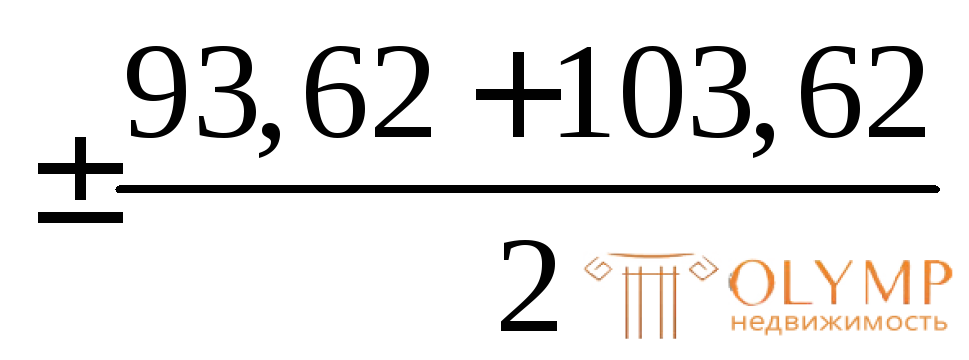==98,62 МПа.

Нормальные напряжения на этих же площадках в соответствии с соотношением (4.13) будут:

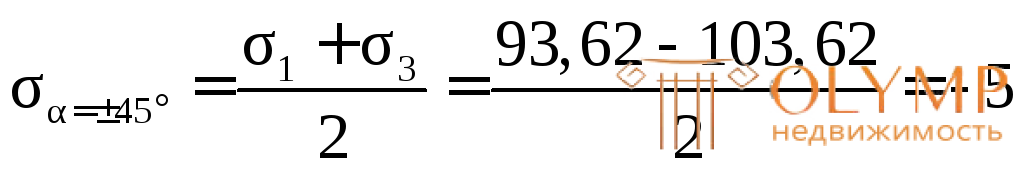МПа.

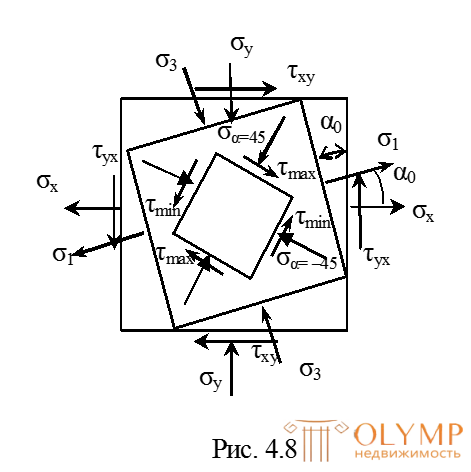
Покажем найденные напряжения на площадках сдвига, наклоненных к главным на 45^o(рис. 4.8).

При этом направления максимального и минимального касательных напряжений покажем так, чтобы они сходились у того ребра элемента, где проходит главное напряжение ₁.

4. Вычисление нормального и касательного напряжений на площадках, наклоненных к заданным на углы = 30и 30+ 90

sin 30^o = 0,5, cos 30^o = 0,866;

cos 60^o = 0,5, sin 60^o = 0,866.

Для этого используем формулы (4.2)–(4.4)

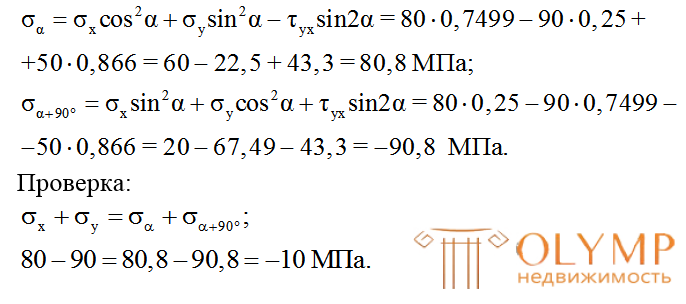
На рис. 4.9 показаны наклонные площадки и напряжения, действующие на этих площадках cучетом их знаков. Угол > 0, поэтому заданные площадки повернуты против хода часовой стрелки.

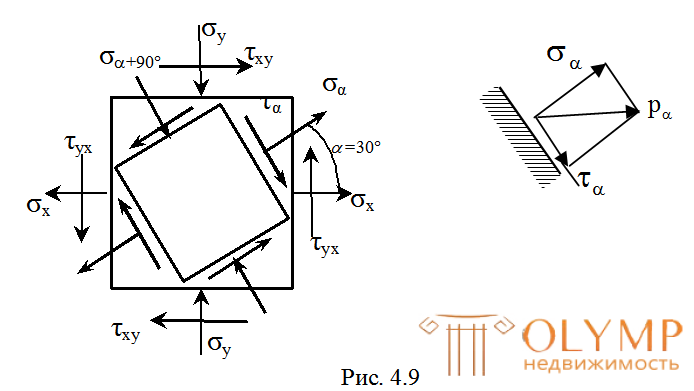
Определим полное напряжение на наклонной площадке:

=

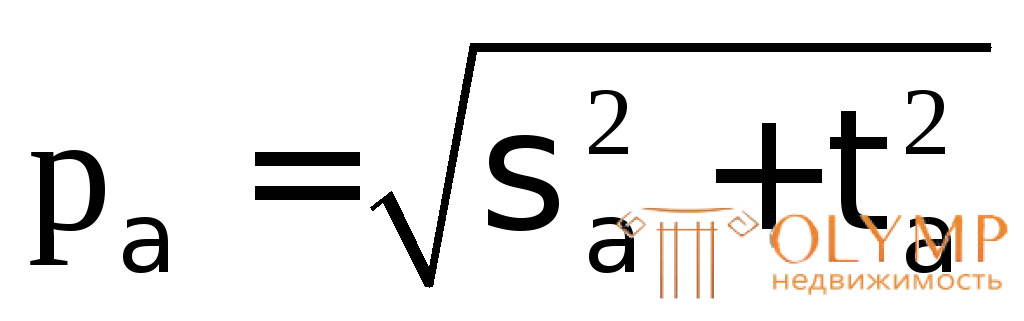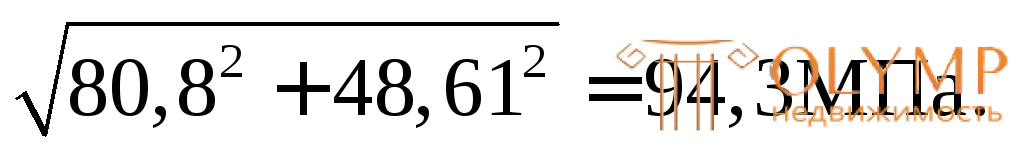
Относительную деформацию по направлению напряжения _определим по формуле

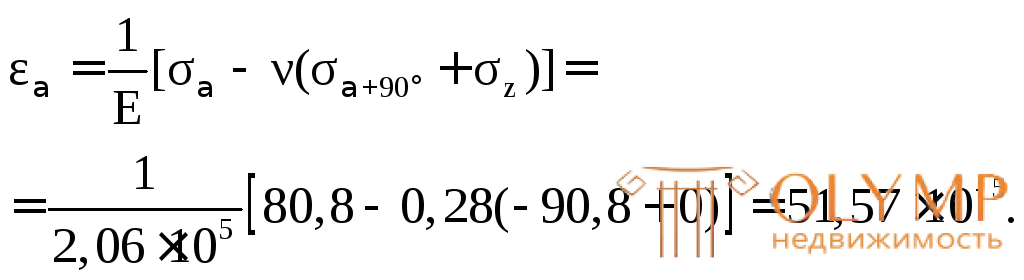
5. Определение расчетных напряжений по четырем теориям прочности и их сравнение:

1-я теория прочности – теория наибольших нормальных напряжений:

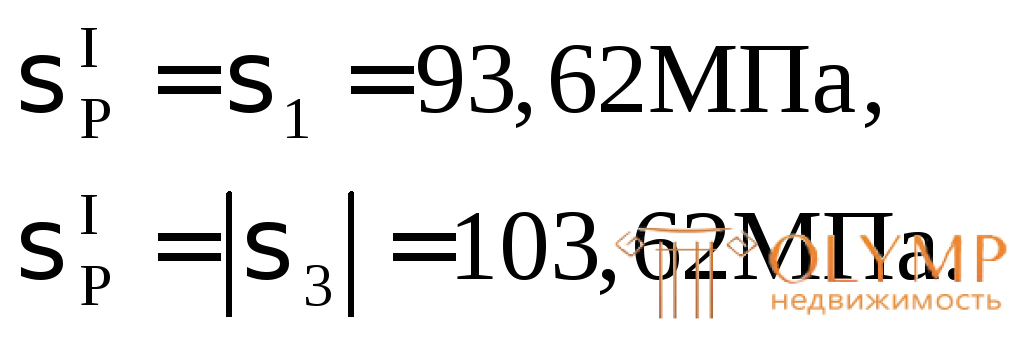
2-я теория прочности – теория наибольших относительных удлинений:

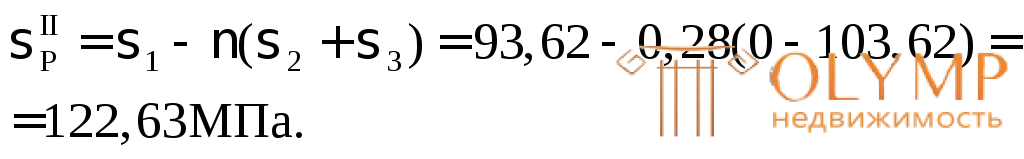
3-я теория прочности – теория наибольших касательных напряжений:

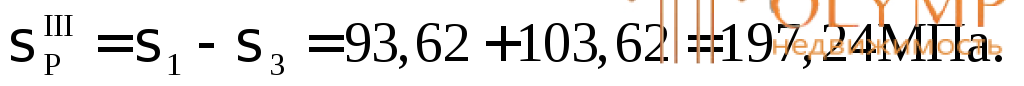
4-я, энергетическая теория прочности:

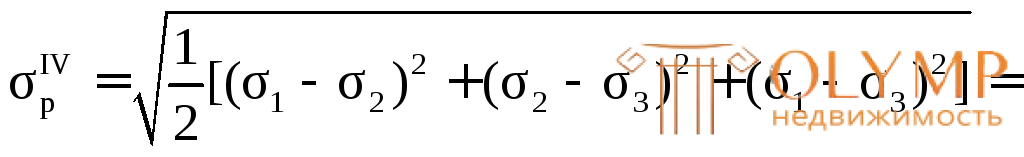
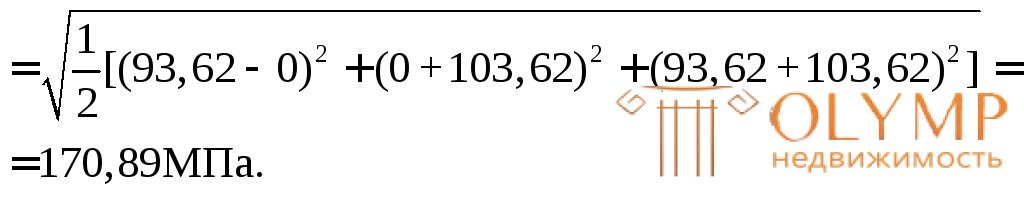
Сравнительный анализ расчетных напряжений 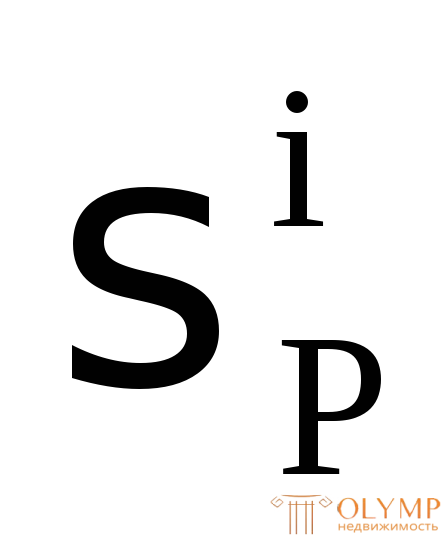показывает, что наибольшее по абсолютной величине расчетное напряжение получается по третьей теории прочности. Значит, если в данном случае использован пластичный материал, то за расчетное напряжение нужно брать это напряжение и условие прочности записать в виде:

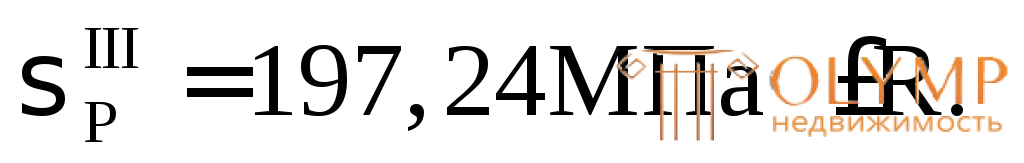
Если же предполагается, что материал хрупкий, то нужно использовать вторую теорию прочности и условие прочности должно быть записано в виде:

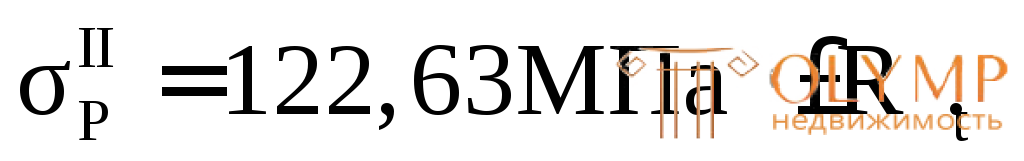
+6. Вычислим относительные деформации по направлениям главных напряжений (главные деформации), используя формулы обобщенного закона Гука (4.22):

Контрольные вопросы по теме

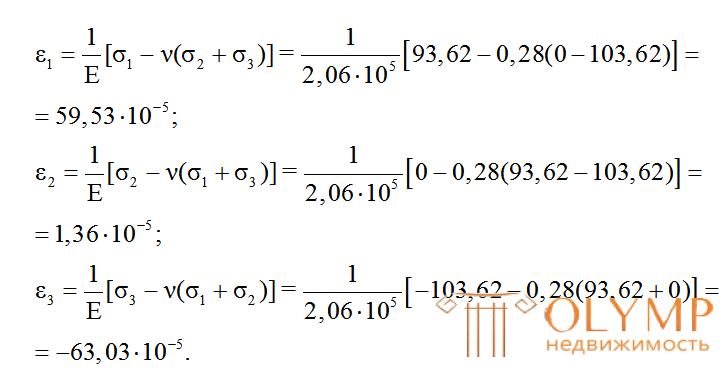
1. Что называется напряженным состоянием в точке? Назовите типы напряженных состояний.

2. Какие площадки называются главными?

3. Какие напряжения называются главными напряжениями?

4. Как определяется положение главных площадок в случае плоского напряженного состояния?

5. Как определяются величины главных напряжений в случае плоского напряженного состояния?

6. Как можно ориентировочно (без расчета) показать линию действия наибольшего главного напряжения, отличного от нуля, в случае плоского напряженного состояния?

7. Как определяются величины экстремальных касательных напряжений ? Как ориентированы эти площадки относительно главных?

8. Сформулируйте "Закон парности касательных напряжений".

9. Как определяются нормальные и касательные напряжения на наклонных площадках в случае плоского напряженного состояния?

10. В чем состоит смысл обобщенного закона Гука? Запишите соотношения, характеризующие этот закон.

11. Как определяется относительная деформация по заданному направлению?

12. Чем вызвано создание теорий прочности? Приведите формулировки и необходимые формулы для 14-й теорий прочности. Укажите преимущества и недостатки каждой теории.

13. Что называется тензором напряжений? Запишите тензор напряжений для объемного напряженного состояния.

14. Как понимаете деформационное и напряженное состояния в точке?

15. Назовите инварианты тензора напряжений в случае объемного напряженного состояния.

16. Как определяется коэффициент Пуассона?

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.