Понятие об объемной деформации. Потенциальная энергия деформации

Объемная деформация - это изменение объема материала под воздействием внешних сил или температурных изменений. Она может проявляться как увеличение или уменьшение объема материала в зависимости от приложенных воздействий. Например, при сжатии материала его объем уменьшается, а при растяжении - увеличивается. Это понятие широко используется в различных областях, таких как инженерия, строительство, материаловедение, стоматология, железнодорожный транспорт и другие.

Из формул (4.22) и (4.23) (см. предыдущую лекции) видно, что относительная деформация имеет место во всех направлениях не только в случае объемного напряженного состояния, но и линейного, и плоского.

Например, если главное напряжение σ₂равно нулю, то деформация в направлении нормали по площадке с нулевым напряжением будет равна:

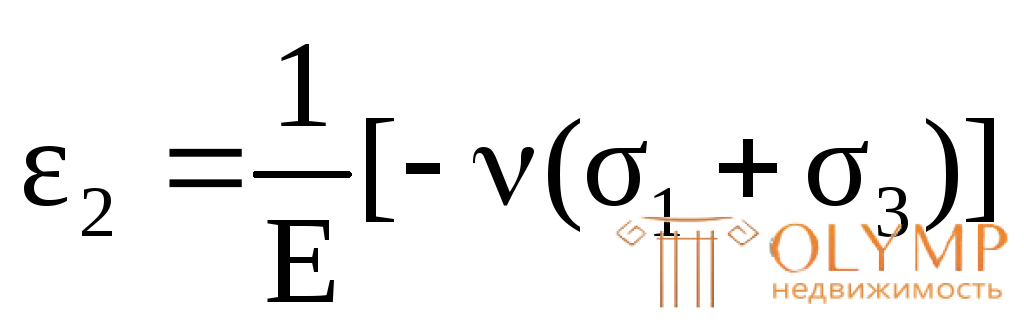. (4.24)

Под действием внешней нагрузки упругое тело деформируется, его объем изменяется и в нем накапливается потенциальная энергия. В процессе разгружения тела потенциальная энергия проявляется в виде работы, совершаемой внутренними силами. Для определения изменения объема тела и количества накопленной им потенциальной энергии необходимо знать изменение объема и количества энергии в каждой частице тела. Приведем соответствующие формулы без подробного вывода.

Относительное изменение объема определится по формуле:

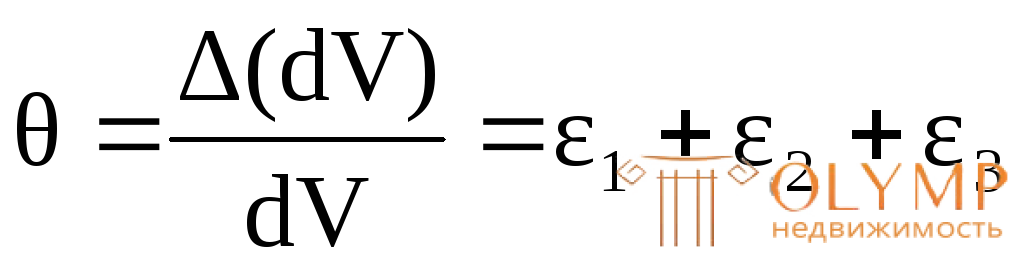. (4.25)

После подстановки в формулу (4.25) вместо ε₁, ε₂ и ε₃ их выражений из (4.22), получим:

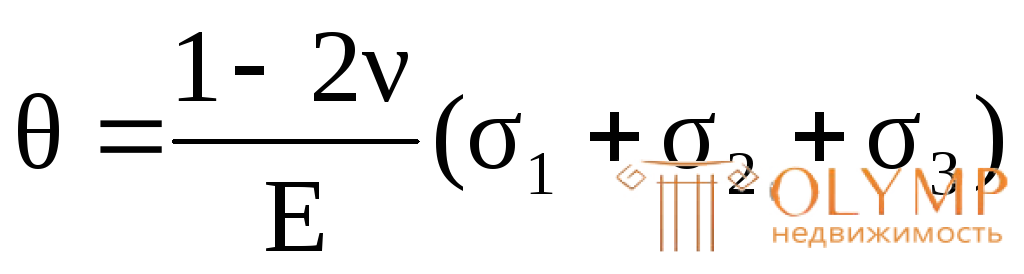. (4.26)

В формулу (4.26) входит сумма главных напряжений. Вместо нее можно подставить сумму (σ_х + σ_у + σ_z), так как они равны.

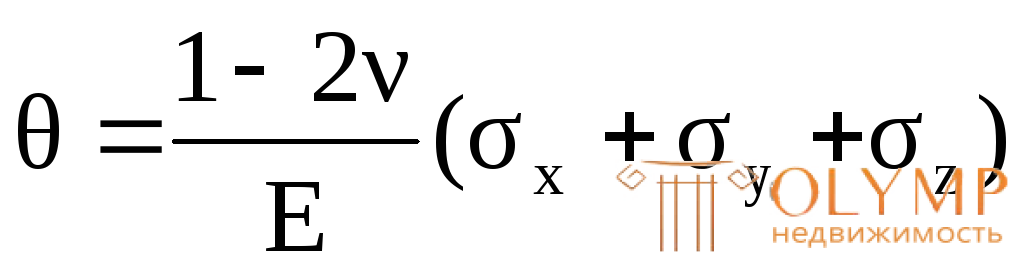. (4.27)

Формулы (4.26) и (4.27) выражают объемный закон Гука.

Если в случае пространственного напряженного состояния σ₁= σ₂= σ₃= σ > 0 (пространственное равномерное растяжение), то на основании формулы (4.26)относительное изменение объемаравно:

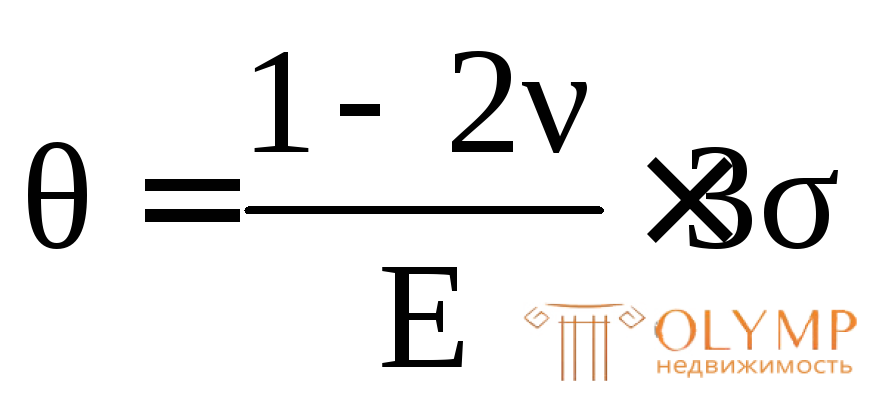. (4.28)

В соответствии с законом сохранения энергии потенциальная энергия деформации элементарного параллелепипеда равна работе внешних сил, приложенных к его граням. При вычислении этой работы будем предполагать, что все внешние силы одновременно постепенно нарастают от нуля до своего конечного значения, т.е. что эти силы действуют статически.

Полная удельная потенциальная энергия деформацииопределится по формуле:

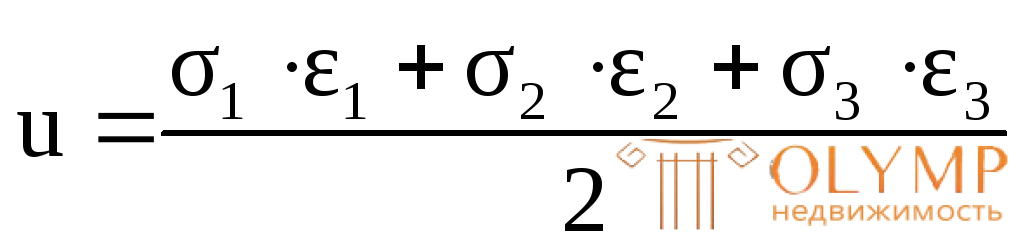. (4.29)

Заменим в этой формуле относительные деформации их выражениями через обобщенный закон Гука из (4.22):

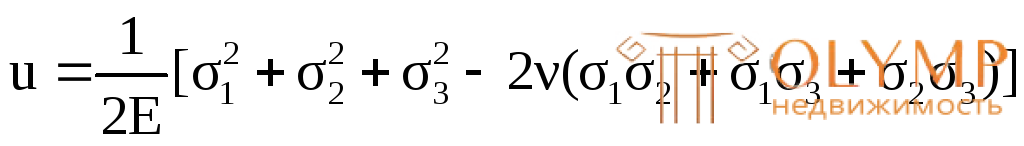. (4.30)

Удельная потенциальная энергия выражается в Дж/м³или Н·м/м³.

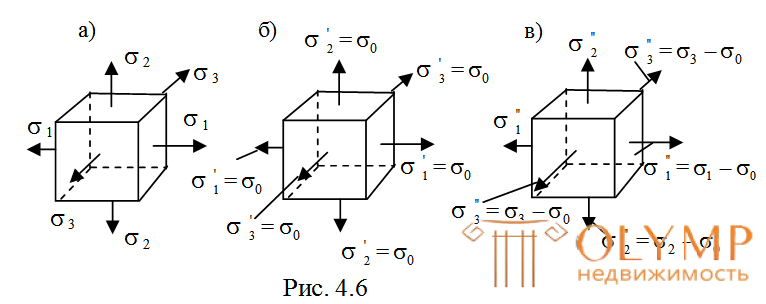
Объемное напряженное состояние можно расчленить на два напряженных состояния. В одном из них объемпараллелепипеда изменяется, а форма его остается неизменной(рис. 4.6б); потенциальная энергия, накопленная в этом состоянии, называетсяпотенциальной энергией изменения объема.

Во втором состоянии (рис. 4.6в) объем элемента не изменяется, аизменяется лишь его форма; потенциальная энергия, накопленная в этом состоянии, называетсяпотенциальной энергией изменения формы.

Для того, чтобы получить выражение удельной потенциальной энергии изменения объема, подставим в формулу (4.30) напряжения

.

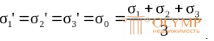После преобразований получим:

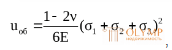, (4.31)

или 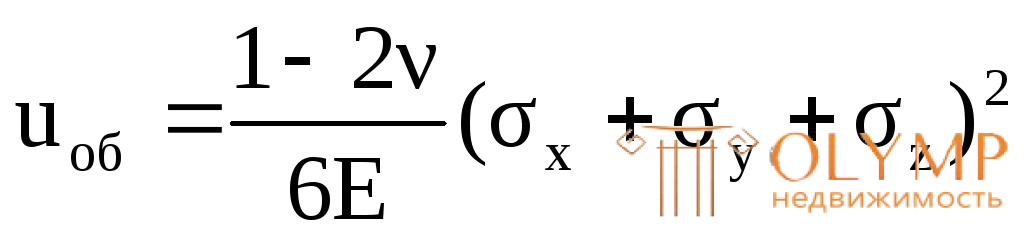. (4.32)

Для получения удельной потенциальной энергии изменения формы, подставим в правую часть формулы (4.30) напряжения (по рис. 4.6в)

– σ₁" = σ₁ – σ₀; σ₂" = σ₂ – σ₀; σ₃" = σ₃ – σ₀.

В результате получим:

.

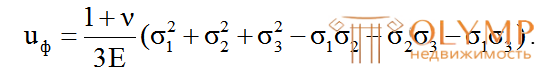После элементарных преобразований последнее соотношение перепишется:

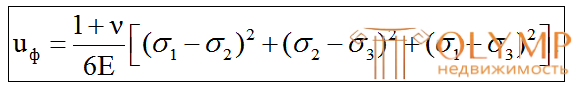(4.33)