3.1. Concrete elements are calculated based on the strength of the action of longitudinal compressive forces, bending moments and shear forces, as well as local compression
3.2. Concrete elements, depending on their working conditions and requirements for them, are calculated without taking into account or taking into account the concrete resistance of the stretched zone.
Without taking into account the resistance of concrete of the stretched zone, the calculation of eccentrically compressed elements specified in section 1.4, a, assuming that the achievement of the limit state is characterized by the destruction of compressed concrete.
Taking into account the resistance of the concrete of the stretched zone, the elements specified in section 1.4b are calculated, as well as elements that do not allow cracks on the operating conditions of the structures (elements subjected to water pressure, cornices, parapets, etc.). At the same time, it is assumed that the limiting state is characterized by the achievement of limiting efforts in the concrete of the stretched zone.
3.3. If forces (moment, lateral force or longitudinal force) F1 from constant and long-lasting loads exceed 0.9 forces from all loads, including short-term ones, you should calculate for the action of forces F1, taking the calculated resistances of concrete Rb and Rbt taking into account the coefficient γb1 = 0 ,9.
3.4. The calculation of the strength of concrete elements on the action of local compression produced in accordance with the instructions of PP.3.81 and 3.82.
3.5. In the concrete elements in the cases specified in paragraph 5.12, it is necessary to provide constructive reinforcement.
3.6. When calculating eccentrically compressed concrete elements, one should take into account the random eccentricity ea taken at least:
1/600 of the length of the element or the distance between its sections, fixed from displacement;
1/30 of the section height;
10 mm.
For elements of statically indefinable constructions (for example, pillars clamped at the ends), the value of the eccentricity of the longitudinal force relative to the center of gravity of the section eo is equal to the value of the eccentricity obtained from the static calculation, but not less than ea.
For elements of statically definable structures, the eccentricity eo is taken to be equal to the sum of eccentricities - from the static calculation of structures and random.
3.7. With the flexibility of lo / i elements> 14 (for a rectangular cross section with lo / h > 4), it is necessary to take into account the effect on their bearing capacity of deflections by multiplying the values of ео by the coefficient η , determined according to p.3.10.
3.8. The calculation of eccentrically compressed concrete elements at the location of the longitudinal force within the section of the element is carried out without taking into account the concrete resistance of the stretched zone as follows.
For elements of rectangular, T-shaped and I-beam sections under the action of a force in the plane of symmetry, the calculation is made from the condition
N £ RbAb , (3.1)
where Ai is the area of the compressed zone of concrete, determined from the condition that its center of gravity coincides with the point of application of the longitudinal force N (taking into account the deflection) (Fig. 3.1.).
For elements of rectangular cross section
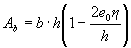(3.2)
where η - see p.3.10.
From condition (3.1), it is also possible to calculate symmetric trapezoidal and triangular sections, if the greatest compression falls on the larger side of the section.
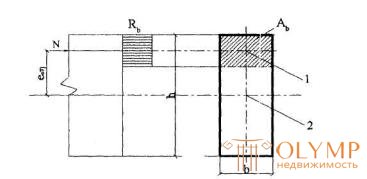
Figure 3.1. Diagram of stresses and stress diagram in cross section, normal to the longitudinal axis of an eccentrically compressed concrete element, calculated by strength without taking into account the concrete resistance of the stretched zone
1-center of gravity of the area of the compressed zone A, 2, the same, the area of the whole section
In other cases, the calculation is made on the basis of the nonlinear deformation model in accordance with PP.3.72 - 3.76, taking into account the calculated dependencies the area of the reinforcement is zero.
It is allowed for oblique eccentric compression of a rectangular section to be calculated from condition (3.1), determining Ау by the formula
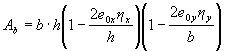(3.3)
where е0 x and в0у are eccentricities of the force N in the direction of the section size h and b, respectively .
η х and η у are coefficients η determined according to clause 3.10 separately for each direction.
3.9. The centrifugal concrete elements at the location of the longitudinal force outside the cross section of the element, as well as elements in which the appearance of cracks is not allowed, regardless of the calculation of condition (3.1), should be checked with regard to the concrete resistance of the stretched zone of the condition
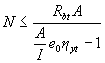, (3.4)
where yt is the distance from the center of gravity of the section of the element to the most stretched fiber;
η - see p.3.10.
For elements of rectangular section condition (3.4) has the form
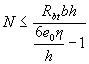(3.5)
It is allowed to calculate concrete elements taking into account the concrete of the stretched zone on the basis of a non-linear deformation model in accordance with PP.3.72 - 3.76, taking into account the calculated dependencies the area of the reinforcement is zero.
3.10. The value of the coefficient η, taking into account the effect of deflection on the value of the eccentricity of the longitudinal force e o, is determined by the formula
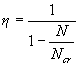(3.6)
where Ncr is the conditional critical force determined by the formula
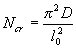(3.7)
where D is the stiffness of the element in the ultimate in strength stage, determined by the formula
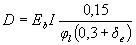(3.8)
Lo = is determined by table 3.1.
Table 3.1.
The nature of the bearing walls and pillars | Estimated length l о of eccentrically compressed concrete elements |
1. With supports at the top and bottom: | |
a) with hinges at two ends, regardless of the amount of displacement of the supports | H |
b) in case of pinching one of the ends and possible displacement of the building supports: | |
multi-span | 1.2 H |
single-span | 1.5 H |
c) with partial pinching of fixed supports | 0.8 H |
2. Free-standing | 2 H |
Note. H is the distance between the overlappings and other horizontal supports (for overlaps monolithically connected with the wall (column) minus the overlap thickness) or the height of a free-standing structure. | |
For rectangular elements, the formula (3.8) is
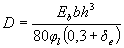(3.8a)
In formulas (3.8) and (3.8a):
j l - coefficient taking into account the effect of long-term load on the deflection of the element in the limit state, equal to
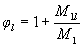(3.9)
but no more than 2;
M1 is the moment relative to the stretched or least compressed face of the section from the action of constant, long-term and short-term loads;
M1 l - the same, from constant and long loads;
d e is the coefficient taken to be equal to eo / h , but not less than 0.15.
For walls and pillars with elastically fixed supports, the indicated value of η is taken into account when calculating sections in the middle third of the height N. When calculating the reference sections, it is assumed η = 1.0, and in other sections by linear interpolation.
If the lower support is rigidly clamped, then with an elastic upper support, the value of η determined by the formula (3.6) is assumed for sections of the lower section with a height of 2/3 H.
3.11. The calculation taking into account the deflection of eccentrically compressed rectangular concrete elements of a class not exceeding B20 at lо £ 20 h is allowed to be made from the condition
N £ αnRbh, (3.10)
where αn is determined by the graph (Fig. 3.2) depending on the values of eo / h and λ = lо h .
3.12. Under the action of significant transverse forces, the condition
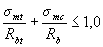(3.11)
where σmt and σts are the main tensile and main compressive stresses determined by the formula
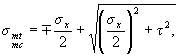(3.12)
σх and τ are the normal and shear stresses in the considered fiber of the section, defined as for an elastic material.
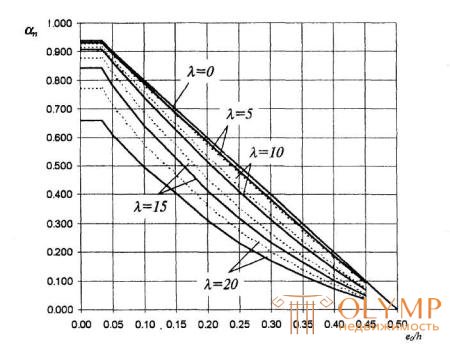
Figure 3.2. Graph of bearing capacity of eccentrically compressed concrete elements
For a rectangular section, the condition (3.11) is checked for fiber at the level of the center of gravity of the section, and for tee and I-sections at the level of junction of the compressed shelves to the wall of the section.
3.13. The calculation of bent concrete elements should be made from the condition
M £ RbtW , (3.13)
where W is the moment of resistance for the extreme stretched fiber; for rectangular section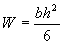 
.
In addition, for the elements of T-section and I-sections, the condition
τ ≤ Rbt (3.14)
where τ is the tangential stresses, defined as for an elastic material at the level of the center of gravity of the section.
Example 1 Given : interroom concrete panel with a thickness of h = 150 mm and height H = 2.7 m, made vertically (in a cassette); concrete class B15 ( E b = 24000 MPa, Rb = 8.5 MPa); full load per 1 m of wall N = 700 kN, including permanent and continuous load Nl = 650 kN.
Required to check the strength of the panel.
The calculation is made according to p.3.8. on the action of a longitudinal force applied with a random eccentricity ea , determined in accordance with clause 3.6.
Insofar as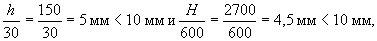 
take ea = e o = 10 mm. The fastening of the panel at the top and bottom is assumed to be hinged, therefore, the calculated length lо , according to Table 3.1, is equal to lо = Н = 2.7 m. Since the ratio lо / h = 2.7 / 0.15 = 18> 4, the calculation is made taking into account the effect of deflection according to p.3.10.
According to the formula (3.9) we determine the coefficient φ l, taking M 1 l / M1 = Nl / N = 650/700 = 0.93,
φ l = 1 + M 1 l / М1 = 1 + 0.93 = 1.93.
Since eo / h = 10/150 = 0.067 <0.15, we take δe = 0.15.
The stiffness D is determined by the formula (3.8a), taking the width of the cross section b = 1 m = 1000 mm
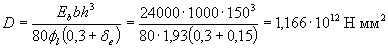
Then
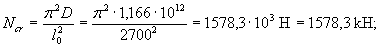
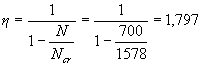
The design resistance of concrete Rb according to clause 2.8 is taken taking into account the coefficients γ b2 = 0.9 and γ b3 = 0.9, and taking into account the presence of short-term loads, we take γ b1 = 1.0. Then Rb = 8.5 · 0.9 · 0.9 = 6.89 MPa.
Check the condition (3.1) using the formula (3.2)
RbAb = Rbbh (1 - 2 · e0 · η / h ) = 6.89 · 1000 · 150 (1 - 2 · 0.067 · 4.797) = 784635 H = 784.6 kN> N = 700 kN, i.e. the strength of the panel on the effect of full load is provided.
Since Nl / N = 0.93> 0.9, according to p.3.3, we check the strength of the panel under the action of only constant and long-lasting loads, i.e. with N = 650 kN. In this case, φ l = 2, and then
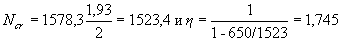
The calculated resistance Rb is taken with γ b1 = 0.9: Rb = 6.89 · 0.9 = 6.2 N.
RbAb = 6.2 · 1000 · 150 (1-2 · 10 · 1,745 / 150) = 713620H = 713.6 kN> N = 650 kN,
those. the strength of the panel is ensured at any combination of loads.
Что бы оставить комментарий войдите
Комментарии (0)