Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
To collect the load on the beam, you need to cut from it 1pm and load
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
When calculating bending rectangular elements with a single reinforcement, there are 3 types of tasks:
Предложить исправление Сохранить Отменить
Type 1
Предложить исправление Сохранить Отменить
Given
Предложить исправление Сохранить Отменить
The dimensions of the section b * h (see), a, M, Yвi, the class of concrete and the class of reinforcement. It is required to determine As and construct the section.
Предложить исправление Сохранить Отменить
Decision:
Предложить исправление Сохранить Отменить
1. According to Vol. 2.3 [Ts.] P. 63 we define Rb (MPa)
Предложить исправление Сохранить Отменить
2. According to V. 2.8 [C.] p. 73 we define Rs (MPa)
Предложить исправление Сохранить Отменить
3. Determine the working height of the section ho = h
Предложить исправление Сохранить Отменить
4. Calculate Ao; Ao = M / Rb ho2 b
Предложить исправление Сохранить Отменить
5. According to t. 3.2 [C.] p.90, taking into account the class of concrete, steel, we find Aomax
Предложить исправление Сохранить Отменить
6. Comparing the values of Ao and Ao max, if Ao £ Ao max, then we have a single reinforcement.
Предложить исправление Сохранить Отменить
7. According to the found value of Ao by m. 3.1 [C.], we find
Предложить исправление Сохранить Отменить
8. Determine the required cross-sectional area of reinforcement As: As = M /
Предложить исправление Сохранить Отменить
9. According to Appendix 2 [C.] p.431, we take the required number of rods and ¯ reinforcement, taking into account that the accepted area of reinforcement must be equal to, or somewhat larger than, the area of reinforcement obtained by calculation.
Предложить исправление Сохранить Отменить
10. Construct a section.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Type I task .
Предложить исправление Сохранить Отменить
Given:
Предложить исправление Сохранить Отменить
Sizes of section b * h = 20 * 40 (see),
Предложить исправление Сохранить Отменить
a = Zsm.
Предложить исправление Сохранить Отменить
M = 110 kNm
Предложить исправление Сохранить Отменить
Concrete class B20; Yi = 0.9
Предложить исправление Сохранить Отменить
steel grade A II.
Предложить исправление Сохранить Отменить
Determine the required amount of reinforcement and to construct the section.
Предложить исправление Сохранить Отменить
Decision:
Предложить исправление Сохранить Отменить
Rb = 11.5 0.9 = 10.35 mPa,
Предложить исправление Сохранить Отменить
Rs = 280mPa,
Предложить исправление Сохранить Отменить
ho = ha = 40-3 = 37 cm
Предложить исправление Сохранить Отменить
Ao = 110 • 105 / 10.35•20•372 (100) = 0.0388 <Ao max = 0.43
Предложить исправление Сохранить Отменить
Ao = 0.0388 =>
Предложить исправление Сохранить Отменить
As = 110 • 105 / 0.995 • 280 • 37 (100) = 14.4 cm2.
Предложить исправление Сохранить Отменить
Accept 3 ¯ 25 A II with Asfact = 14.43 cm2.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Type 2
Предложить исправление Сохранить Отменить
Given:
Предложить исправление Сохранить Отменить
The dimensions of the cross section b * h, the value of a, the coefficient of the working condition Ybi
Предложить исправление Сохранить Отменить
Bending moment M, class of concrete and reinforcement, area of tensile reinforcement As.
Предложить исправление Сохранить Отменить
Determine M £ Msech?
Предложить исправление Сохранить Отменить
Decision:
Предложить исправление Сохранить Отменить
1. According to the table. 13 SniP 2.03.01-84 or m. 2.3 [C.] we find the value of Rb (mPa)
Предложить исправление Сохранить Отменить
2. According to the table. 2.8 [C.] => Rs.
Предложить исправление Сохранить Отменить
3. Determine the working height of the section ho = h - a
Предложить исправление Сохранить Отменить
4. Determine the height of the compressed zone section: x = RsAs / Rbb
Предложить исправление Сохранить Отменить
5. Determine the relative height of the compressed zone of concrete.
Предложить исправление Сохранить Отменить
6. According to table. 3.2 [C.] p.90, taking into account the class of concrete and reinforcement, we find the value of the boundary height of the compressed zone of concrete |
Предложить исправление Сохранить Отменить
7. If
Предложить исправление Сохранить Отменить
M £ RsAs (ho - 0,5x)
Предложить исправление Сохранить Отменить
8. We conclude about the bearing capacity of the element. (This calculation is typical for major repairs)
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Problem number 2
Предложить исправление Сохранить Отменить
Given:
Предложить исправление Сохранить Отменить
Dimensions sech. b * h = 30 * 60 (see); a = 3 (see); Yi = 0.9; M = 160 kNm;
Предложить исправление Сохранить Отменить
concrete class B40. reinforcement class A II, reinforcement quantity 4 ¯ 22
Предложить исправление Сохранить Отменить
with As fact. = 15.2 cm2.
Предложить исправление Сохранить Отменить
Check: M £ Msech
Предложить исправление Сохранить Отменить
Decision:
Предложить исправление Сохранить Отменить
Rb = 22 * 0.9 = 19.8 MPa; Rs = 280 MPa;
Предложить исправление Сохранить Отменить
ho = h - a = 60 - 3 = 57 cm.
Предложить исправление Сохранить Отменить
x = RsAs / Rbb = 280 * 15.2 / 19.8 * 30 = 7.16 cm.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
= x / ho = 7.16 / 57.5 = 0.1245 <
Предложить исправление Сохранить Отменить
Msech = RsAs (ho - 0.5x) = 280 * 15.2 * (57.5 - 0.5 * 7.16) * (100) = 22948000 Ncm = 229.48 kNm
Предложить исправление Сохранить Отменить
M = 160 <MSt = 229.48 kNm - the cross section strength is ensured.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Problem number 3
Предложить исправление Сохранить Отменить
Given:
Предложить исправление Сохранить Отменить
Dimensions sech. b * h = 32 * 68 (cm), a = 3.8 cm, B20; Yi = 0.9; M = 205 kNm; reinforcement class A III, As = 10.05 cm2. Identify: M £ Msech
Предложить исправление Сохранить Отменить
Decision:
Предложить исправление Сохранить Отменить
Rb = 11.5 * 0.9 = 10.35 MPa, Rs = 365 MPa,
Предложить исправление Сохранить Отменить
ho = ha = 68-3.8 = 64.2 cm.
Предложить исправление Сохранить Отменить
x = Rs * As / Rb * b = 365 * 10.05 / 10.35 * 32 = 11.075 cm.
Предложить исправление Сохранить Отменить
Msech = RsAs (ho - 0.5x) = 365 (100) 10.05 (64.2 - 0.5 * 11.075) = 21518000 Ncm 215 kNm.
Предложить исправление Сохранить Отменить
M = 215> Msec = 205 KN m - cross section strength is not ensured, it is necessary to reinforce additionally => by
Предложить исправление Сохранить Отменить
As = 215 * 105 / 0.9052 * 365 * 64.2 * (100) = 10.4 cm2. We take 3 22 22 A III with As = 11.4 cm2.
Предложить исправление Сохранить Отменить
T ipa 3
Предложить исправление Сохранить Отменить
Task number 4
Предложить исправление Сохранить Отменить
This type of tasks is adopted in the calculation of new designs, or reconstruction, in the case of replacement of elements.
Предложить исправление Сохранить Отменить
Given:
Предложить исправление Сохранить Отменить
B 30, Yvi = 0.9; M = 90kNm, a = 3.2 cm., Rebar class AIII;
Предложить исправление Сохранить Отменить
Define: As; b; h.
Предложить исправление Сохранить Отменить
Decision:
Предложить исправление Сохранить Отменить
1. By tab. 2.3 => Rb = Rb * Yi = 17 * 0.9 = 15.3 MPa.
Предложить исправление Сохранить Отменить
2. According to tab. 2.8 => Rs = 365 mPa.
Предложить исправление Сохранить Отменить
3. Accept
Предложить исправление Сохранить Отменить
(for plates
Предложить исправление Сохранить Отменить
4. Accept b = 20 ... 40 cm
Предложить исправление Сохранить Отменить
5. According to the table. 3.1 => A0 = 0.219
Предложить исправление Сохранить Отменить
6. Find ho =
Предложить исправление Сохранить Отменить
7. We define h = h0 + a = 36.65 + 3.2 = 39.85 cm round up to 40 cm.
Предложить исправление Сохранить Отменить
8. Specify ho = h = 40-3.2 = 36.8 cm.
Предложить исправление Сохранить Отменить
9. Determine the actual Ao:
Предложить исправление Сохранить Отменить
Ao = M / b ho2 Rb = 90,105 / 20 * 36.82 15.3 = 0.212
Предложить исправление Сохранить Отменить
10. According to Table. 3.2 find Ao max = 0,39
Предложить исправление Сохранить Отменить
Ao = 0,217 <Ao max = 0,39 =>
Предложить исправление Сохранить Отменить
As = M / cm2.
Предложить исправление Сохранить Отменить
Accept 3 ¯ 20 AIII with Asfact = 9.41 cm2.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Calculation of flexible elements of rectangular cross section. (type 1)
Предложить исправление Сохранить Отменить
Find A s
Предложить исправление Сохранить Отменить
No. Var
Предложить исправление Сохранить Отменить
M (kNm)
Предложить исправление Сохранить Отменить
in (cm)
Предложить исправление Сохранить Отменить
h (cm)
Предложить исправление Сохранить Отменить
concrete
Предложить исправление Сохранить Отменить
armature
Предложить исправление Сохранить Отменить
Twi
Предложить исправление Сохранить Отменить
a (cm)
Предложить исправление Сохранить Отменить
l (m)
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
one
Предложить исправление Сохранить Отменить
120
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
8.2
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
2
Предложить исправление Сохранить Отменить
123
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
8.4
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
136
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
42
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
6.3
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
130
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
43
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
9.1
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
five
Предложить исправление Сохранить Отменить
124
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
44
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
7.2
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
132
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
45
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.6
Предложить исправление Сохранить Отменить
5.3
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
7
Предложить исправление Сохранить Отменить
118
Предложить исправление Сохранить Отменить
26
Предложить исправление Сохранить Отменить
46
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.7
Предложить исправление Сохранить Отменить
6.8
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
eight
Предложить исправление Сохранить Отменить
129
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
47
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.8
Предложить исправление Сохранить Отменить
5.9
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
9
Предложить исправление Сохранить Отменить
137
Предложить исправление Сохранить Отменить
27
Предложить исправление Сохранить Отменить
48
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.9
Предложить исправление Сохранить Отменить
7.3.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
119
Предложить исправление Сохранить Отменить
28
Предложить исправление Сохранить Отменить
49
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
4.0
Предложить исправление Сохранить Отменить
5.1
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
121
Предложить исправление Сохранить Отменить
29
Предложить исправление Сохранить Отменить
50
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
5.6
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
127
Предложить исправление Сохранить Отменить
thirty
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
9.4
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
13
Предложить исправление Сохранить Отменить
135
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
9.3
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
140
Предложить исправление Сохранить Отменить
sixteen
Предложить исправление Сохранить Отменить
42
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
10.1
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
141
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
43
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
6.4
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
sixteen
Предложить исправление Сохранить Отменить
142
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
44
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.6
Предложить исправление Сохранить Отменить
8.5
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
143
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
45
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.7
Предложить исправление Сохранить Отменить
9.0
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
144
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
46
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.8
Предложить исправление Сохранить Отменить
7.9
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
145
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
47
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.9
Предложить исправление Сохранить Отменить
4.9
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
149
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
48
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
4.0
Предложить исправление Сохранить Отменить
7.5
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
125
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
49
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
6.2
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
126
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
50
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
8.1
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
129
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
51
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
7.4
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
138
Предложить исправление Сохранить Отменить
26
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
5.3
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
140
Предложить исправление Сохранить Отменить
27
Предложить исправление Сохранить Отменить
52
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
6.0
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Calculation of flexible elements of rectangular cross section.
Предложить исправление Сохранить Отменить
Check M <Msech Type 2
Предложить исправление Сохранить Отменить
No. Var
Предложить исправление Сохранить Отменить
M (kNm)
Предложить исправление Сохранить Отменить
in (cm)
Предложить исправление Сохранить Отменить
h (cm)
Предложить исправление Сохранить Отменить
concrete
Предложить исправление Сохранить Отменить
armature
Предложить исправление Сохранить Отменить
Twi
Предложить исправление Сохранить Отменить
a (cm)
Предложить исправление Сохранить Отменить
l (m)
Предложить исправление Сохранить Отменить
As
Предложить исправление Сохранить Отменить
one
Предложить исправление Сохранить Отменить
120
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
6.0
Предложить исправление Сохранить Отменить
14.3
Предложить исправление Сохранить Отменить
2
Предложить исправление Сохранить Отменить
123
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
6.5
Предложить исправление Сохранить Отменить
11.5
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
136
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
42
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
6.6
Предложить исправление Сохранить Отменить
13.1
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
130
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
43
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
6.7
Предложить исправление Сохранить Отменить
15.4
Предложить исправление Сохранить Отменить
five
Предложить исправление Сохранить Отменить
124
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
44
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
6.8
Предложить исправление Сохранить Отменить
15.2
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
132
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
45
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.6
Предложить исправление Сохранить Отменить
6.9
Предложить исправление Сохранить Отменить
12.9
Предложить исправление Сохранить Отменить
7
Предложить исправление Сохранить Отменить
118
Предложить исправление Сохранить Отменить
26
Предложить исправление Сохранить Отменить
46
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.7
Предложить исправление Сохранить Отменить
7.0
Предложить исправление Сохранить Отменить
11.6
Предложить исправление Сохранить Отменить
eight
Предложить исправление Сохранить Отменить
129
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
47
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.8
Предложить исправление Сохранить Отменить
7.1
Предложить исправление Сохранить Отменить
16,1
Предложить исправление Сохранить Отменить
9
Предложить исправление Сохранить Отменить
137
Предложить исправление Сохранить Отменить
27
Предложить исправление Сохранить Отменить
48
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.9
Предложить исправление Сохранить Отменить
7.2
Предложить исправление Сохранить Отменить
15.3
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
119
Предложить исправление Сохранить Отменить
28
Предложить исправление Сохранить Отменить
49
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
4.0
Предложить исправление Сохранить Отменить
7.3
Предложить исправление Сохранить Отменить
17.2
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
121
Предложить исправление Сохранить Отменить
29
Предложить исправление Сохранить Отменить
50
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
7.4
Предложить исправление Сохранить Отменить
14.6
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
127
Предложить исправление Сохранить Отменить
thirty
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
7.5
Предложить исправление Сохранить Отменить
15.3
Предложить исправление Сохранить Отменить
13
Предложить исправление Сохранить Отменить
135
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
7.6
Предложить исправление Сохранить Отменить
16,1
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
140
Предложить исправление Сохранить Отменить
sixteen
Предложить исправление Сохранить Отменить
42
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
7.7
Предложить исправление Сохранить Отменить
12.8
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
141
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
43
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
7.8
Предложить исправление Сохранить Отменить
13.0
Предложить исправление Сохранить Отменить
sixteen
Предложить исправление Сохранить Отменить
142
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
44
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.6
Предложить исправление Сохранить Отменить
7.9
Предложить исправление Сохранить Отменить
17.0
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
143
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
45
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.7
Предложить исправление Сохранить Отменить
8.0
Предложить исправление Сохранить Отменить
10.9
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
144
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
46
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.8
Предложить исправление Сохранить Отменить
8.1
Предложить исправление Сохранить Отменить
15.1
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
145
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
47
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.9
Предложить исправление Сохранить Отменить
8.2
Предложить исправление Сохранить Отменить
16.3
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
149
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
48
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
4.0
Предложить исправление Сохранить Отменить
8.3
Предложить исправление Сохранить Отменить
14.6
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
125
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
49
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
8.4
Предложить исправление Сохранить Отменить
15.7
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
126
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
50
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
8.5
Предложить исправление Сохранить Отменить
18.2
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
129
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
51
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
8.6
Предложить исправление Сохранить Отменить
18.6
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
138
Предложить исправление Сохранить Отменить
26
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
8.7
Предложить исправление Сохранить Отменить
11.3
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
140
Предложить исправление Сохранить Отменить
27
Предложить исправление Сохранить Отменить
52
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
8.8
Предложить исправление Сохранить Отменить
15.0
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Questions for self-test.
Предложить исправление Сохранить Отменить
1. Estimated concrete compressive strength.
Предложить исправление Сохранить Отменить
2. Estimated resistance of reinforcement tensile.
Предложить исправление Сохранить Отменить
3. Standard concrete resistance to stretching.
Предложить исправление Сохранить Отменить
4. Estimated resistance of concrete to stretching.
Предложить исправление Сохранить Отменить
5. in-
Предложить исправление Сохранить Отменить
6. h-
Предложить исправление Сохранить Отменить
7. h0 =
Предложить исправление Сохранить Отменить
8. a
Предложить исправление Сохранить Отменить
9. As
Предложить исправление Сохранить Отменить
10. Avs
Предложить исправление Сохранить Отменить
11. x =
Предложить исправление Сохранить Отменить
12. Zb =
Предложить исправление Сохранить Отменить
13.
Предложить исправление Сохранить Отменить
14.
Предложить исправление Сохранить Отменить
15. m
Предложить исправление Сохранить Отменить
16. Formula 3
Предложить исправление Сохранить Отменить
17. Formula 4
Предложить исправление Сохранить Отменить
18. Ns =
Предложить исправление Сохранить Отменить
19. Nb =
Предложить исправление Сохранить Отменить
20. What is the basis for the calculation of the 1st, 2nd, 3rd stages of work of the bent elements?
Предложить исправление Сохранить Отменить
Questions for self-monitoring on the topic:
Предложить исправление Сохранить Отменить
"Flexable reinforced concrete elements of rectangular section".
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
1. Types of reinforcement according to the nature of work in bending elements.
Предложить исправление Сохранить Отменить
2. Types of reinforcement by type of surface in bending elements.
Предложить исправление Сохранить Отменить
3. Principles of reinforcement of bent elements of rectangular cross-section.
Предложить исправление Сохранить Отменить
4. What is the percentage of reinforcement bent elements?
Предложить исправление Сохранить Отменить
5. What is the minimum percentage of reinforcement of bent elements?
Предложить исправление Сохранить Отменить
6. At what stage are bent reinforced concrete elements of rectangular cross section calculated?
Предложить исправление Сохранить Отменить
7. What is: c , h, h0 = ha, as, abc, x, z?
Предложить исправление Сохранить Отменить
8. What is equal to the distance a?
Предложить исправление Сохранить Отменить
9. What are the cases of exhaustion of bearing capacity of bent elements?
Предложить исправление Сохранить Отменить
10. Boundary condition between the 1st and 2nd cases of calculation?
Предложить исправление Сохранить Отменить
11. What are the internal forces equal in the limit state?
Предложить исправление Сохранить Отменить
12. What static conditions are used in the calculation of bent elements?
Предложить исправление Сохранить Отменить
13. Formulas for the calculation of bending reinforced concrete elements of rectangular cross section: A0, As ,?
Предложить исправление Сохранить Отменить
14. What are the three types of problems of calculating bent reinforced concrete elements of rectangular section?
Предложить исправление Сохранить Отменить
15. How is the diameter and spacing of transverse reinforcement in a bent reinforced concrete elements of rectangular cross section?
Предложить исправление Сохранить Отменить
16. Types of reinforcement according to the nature of work in bending elements.
Предложить исправление Сохранить Отменить
17. Types of reinforcement by type of surface in bent elements.
Предложить исправление Сохранить Отменить
18. Principles of reinforcement of bent elements of rectangular cross-section.
Предложить исправление Сохранить Отменить
19. What is the percentage of reinforcement of bent elements?
Предложить исправление Сохранить Отменить
20. What is the minimum percentage of reinforcement of bent elements?
Предложить исправление Сохранить Отменить
21. At what stage are bent reinforced concrete elements of rectangular cross section calculated?
Предложить исправление Сохранить Отменить
22. What is: c , h, h0 = ha, as, abc, x, z?
Предложить исправление Сохранить Отменить
23. What is equal to the distance a?
Предложить исправление Сохранить Отменить
24. What are the cases of exhaustion of bearing capacity of bent elements?
Предложить исправление Сохранить Отменить
25. The boundary condition between the 1st and 2nd cases of calculation?
Предложить исправление Сохранить Отменить
26. What are internal forces equal in the limit state?
Предложить исправление Сохранить Отменить
27. What are the static conditions used in the calculation of bent elements?
Предложить исправление Сохранить Отменить
28. Formulas for the calculation of bending reinforced concrete elements of rectangular section: A0, As ,?
Предложить исправление Сохранить Отменить
29. What are the three types of problems of calculating bent reinforced concrete elements of rectangular section?
Предложить исправление Сохранить Отменить
30. How is the diameter and spacing of transverse reinforcement in a bent reinforced concrete elements of rectangular cross section?
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Technical dictation number 1
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
1. Limit - this is the condition of the building structure -
Предложить исправление Сохранить Отменить
2. Calculation for the first group of limit states -
Предложить исправление Сохранить Отменить
3. Calculation for the second group of limit states -
Предложить исправление Сохранить Отменить
four.
Предложить исправление Сохранить Отменить
five.
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
7
Предложить исправление Сохранить Отменить
8. Constant loads -
Предложить исправление Сохранить Отменить
9. Temporary loads -
Предложить исправление Сохранить Отменить
10. Short-term loads -
Предложить исправление Сохранить Отменить
11. Special loads -
Предложить исправление Сохранить Отменить
12. Regulatory loads -
Предложить исправление Сохранить Отменить
13. Design load -
Предложить исправление Сохранить Отменить
14. Rb
Предложить исправление Сохранить Отменить
15. Rs
Предложить исправление Сохранить Отменить
16. Rsp
Предложить исправление Сохранить Отменить
17. RBP
Предложить исправление Сохранить Отменить
18. Rb
Предложить исправление Сохранить Отменить
19. Rbt
Предложить исправление Сохранить Отменить
Technical dictation number 2
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
1. Estimated concrete compressive strength.
Предложить исправление Сохранить Отменить
2. Estimated resistance of reinforcement tensile.
Предложить исправление Сохранить Отменить
3. Standard concrete resistance to stretching.
Предложить исправление Сохранить Отменить
4. Estimated resistance of concrete to stretching.
Предложить исправление Сохранить Отменить
5. in-
Предложить исправление Сохранить Отменить
6. h-
Предложить исправление Сохранить Отменить
7. h0 =
Предложить исправление Сохранить Отменить
8. a
Предложить исправление Сохранить Отменить
9. As
Предложить исправление Сохранить Отменить
10. Avs
Предложить исправление Сохранить Отменить
11. x =
Предложить исправление Сохранить Отменить
12. Zb =
Предложить исправление Сохранить Отменить
13.
Предложить исправление Сохранить Отменить
14.
Предложить исправление Сохранить Отменить
15. m
Предложить исправление Сохранить Отменить
16. Formula 3
Предложить исправление Сохранить Отменить
17. Formula 4
Предложить исправление Сохранить Отменить
18. Ns =
Предложить исправление Сохранить Отменить
19. Nb =
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
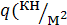
 ) multiply by distance beams, and then calculate the bending moment.
) multiply by distance beams, and then calculate the bending moment. 
 .
.  Rs ho
Rs ho 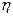 = 0.995
= 0.995 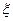 = x / h0.
= x / h0. 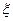 R.
R. 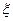 £
£ 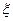 y, then check the strength of the section from the condition:
y, then check the strength of the section from the condition: 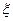 y = 0.52 according to t. 3.2. [P] p.90
y = 0.52 according to t. 3.2. [P] p.90 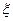 = x / ho = 7.16 / 57.5 = 0.1245 <
= x / ho = 7.16 / 57.5 = 0.1245 < 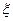 y = 0.52 => single reinforcement.
y = 0.52 => single reinforcement. 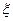 = x / ho = 11.075 / 64.2 = 0.173 <|
= x / ho = 11.075 / 64.2 = 0.173 <| 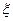 y = 0.59 => single reinforcement.
y = 0.59 => single reinforcement. 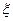 = 0.173 =>
= 0.173 => 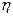 = 0.9052
= 0.9052 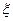 = 0.25 (for beams 0.2 ... 0.4)
= 0.25 (for beams 0.2 ... 0.4) 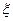 = 0.1 ... 0.15)
= 0.1 ... 0.15) 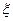 = 0.25
= 0.25 

 M / A 0 * Rb * b =
M / A 0 * Rb * b = 
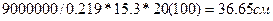
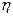 = 0.8775
= 0.8775 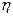 Rs ho = 90 105 /0.8875*365*36,8* (100) = 7.64 cm2.
Rs ho = 90 105 /0.8875*365*36,8* (100) = 7.64 cm2. 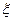 =
= 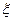 y =
y =  f -
f -  P -
P -  b and
b and  s -
s -  bi and
bi and  si -
si - 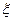 =
= 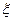 y =
y =
Что бы оставить комментарий войдите
Комментарии (0)