Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Расчет изгибаемых элементов на поперечную силу
Предложить исправление Сохранить Отменить
Расчет прочности изгибаемых элементов по наклонным сечениям.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
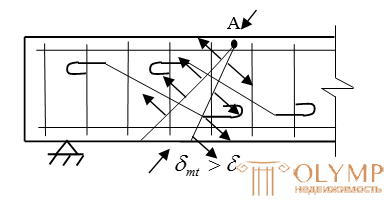
Опыты показывают, что наклонные трещины могут возникать вблизи опор в результате совместного действия изгибающего момента и поперечной силы. Из курса сопротивления материалов известно, что изгибающий момент М вызывает в сечении балки нормальные напряжения
Предложить исправление Сохранить Отменить
При дальнейшем возрастании нагрузки происходят разрушение элемента по наклонному сечению (стадия III).
Предложить исправление Сохранить Отменить
Расчет на действие наклонных сжимающих напряжений.
Предложить исправление Сохранить Отменить
При образовании наклонных трещин бетон между ними испытывает действие главных сжимающих напряжений и одновременно растягивающих усилий от поперечной арматуры.
Предложить исправление Сохранить Отменить
Для обеспечения прочности бетона на сжатие в полосе между наклонными трещинами должно соблюдаться условие:
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
где
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Danger dungeon quest
Game: Perform tasks and rest cool.7 people play!
Play game
Если условие (1) не выполняется, необходимо увеличить размеры сечения, или повысить класс бетона.
Предложить исправление Сохранить Отменить
Наклонная трещина в сечении не образуется, если
Предложить исправление Сохранить Отменить
Этому условию соответствует приближенная опытная зависимость:
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
где
Предложить исправление Сохранить Отменить
Danger dungeon quest
Game: Perform tasks and rest cool.7 people play!
Play game
При соблюдении условия (2) расчет наклонных сечений поперечной силе не требуется, и арматура может быть назначена по конструктивным соображениям. Если же условие (2) не выполняется, то прочность сечения нужно обеспечить постановкой поперечной арматуры в соответствии с расчетом (см. блок-схему).
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Конструктивные требования
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
В соответствии со СНиП расстояние между поперечными стержнями в элементах, определяемое по конструктивным соображениям, принимают:
Предложить исправление Сохранить Отменить
а) На приопорных участках, равных 1/4
Предложить исправление Сохранить Отменить
для балок при h
Предложить исправление Сохранить Отменить
б) Для балок при h >450мм =>
Предложить исправление Сохранить Отменить
в) На остальной части пролета при любой высоте h
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Диаметр поперечных стержней принимается по таблице “Соотношения стержней” из условия технологии сварки.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Эпюра материалов.
Предложить исправление Сохранить Отменить
В целях экономии металла часть продольной арматуры может не доводиться до опоры и отбрасываться в пролете там, где она не требуется по расчету. В этом случае раст. степени должно заводиться за точку теоретического обрыва ( т.е. за сеч. 1-1, в котором эти степени не требуются по расчету), на длину не < 20d (где d-диаметр обрываемого стержня).
Предложить исправление Сохранить Отменить
Места теоретического обрыва стержней устанавливают графо-аналитическим способом. С этой целью на эпюру изгибающих моментов от внешней нагрузки наносят в том же масштабе эпюру моментов, воспринимаемых сечением элемента с фактически имеющейся растянутой арматурой. Пусть, например, в балке по наибольшему моменту подобрана арматура из 4-х стержней 1,2,3,4
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Два из них. 1 и 2 доводят до опоры, а стержней 3 и4 обрывают в пролете. Для определения места их теоретического обрыва на графике в принятом масштабе откладывают момент, воспринимаемый сечением, армированными стержнями 1 и 2 с площадью
Предложить исправление Сохранить Отменить
Пример № 1
Предложить исправление Сохранить Отменить
Danger dungeon quest
Game: Perform tasks and rest cool.7 people play!
Play game
Дано : Q=25кН
Предложить исправление Сохранить Отменить
b=20см
Предложить исправление Сохранить Отменить
h=45см
Предложить исправление Сохранить Отменить
a=3см
Предложить исправление Сохранить Отменить
B20 ; γbi=1
Предложить исправление Сохранить Отменить
продольная арматура
Предложить исправление Сохранить Отменить
Danger dungeon quest
Game: Perform tasks and rest cool.7 people play!
Play game
2
20 AIII
Предложить исправление Сохранить Отменить
Rb=11,5мПа
Предложить исправление Сохранить Отменить
Rbt=0,9мПа
Предложить исправление Сохранить Отменить
Rsw=175мПа
Предложить исправление Сохранить Отменить
Q=25кН
Предложить исправление Сохранить Отменить
Es=2,0
Предложить исправление Сохранить Отменить
Eb=27
Предложить исправление Сохранить Отменить
Проверить прочность сечения
Предложить исправление Сохранить Отменить
Решение:
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Определяем по конструктивным требованиям
Предложить исправление Сохранить Отменить
1) n=2; dsw=6 AI, т.к. h=45, => Sw=
Предложить исправление Сохранить Отменить
2)
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
3) вычисляем
Предложить исправление Сохранить Отменить
4) вычисляем
Предложить исправление Сохранить Отменить
5)
Предложить исправление Сохранить Отменить
6) проверяем условие
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Вывод: наклонные трещины не образуются и прочность наклонного сечения на действие поперечной силы обеспечена.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Пример№2
Предложить исправление Сохранить Отменить
Дано: Q= 100кН
Предложить исправление Сохранить Отменить
Проверяем условие
Предложить исправление Сохранить Отменить
Danger dungeon quest
Game: Perform tasks and rest cool.7 people play!
Play game
100Н>45.4кН – условие не выполняется, переходим к следующему этапу:
Предложить исправление Сохранить Отменить
7) вычисляем
Предложить исправление Сохранить Отменить
8) вычисляем
Предложить исправление Сохранить Отменить
Danger dungeon quest
Game: Perform tasks and rest cool.7 people play!
Play game
9) проверяем условие:
Предложить исправление Сохранить Отменить
Вывод: прочность наклонного сечения на действие поперечной силы обеспечена.
Предложить исправление Сохранить Отменить
Пример№3
Предложить исправление Сохранить Отменить
Поперечная сила Q=150кН
Предложить исправление Сохранить Отменить
9) проверяем условие:
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
150>110 => условие не выполняется, поэтому уменьшаем шаг поперечных стержней Sw=100мм
Предложить исправление Сохранить Отменить
3) вычисляем:
Предложить исправление Сохранить Отменить
4)
Предложить исправление Сохранить Отменить
5) Проверяем:
Предложить исправление Сохранить Отменить
150<363 => наклонные трещины не образуются.
Предложить исправление Сохранить Отменить
6) Условие пункта 6 не выполняется
Предложить исправление Сохранить Отменить
150>45.4
Предложить исправление Сохранить Отменить
7) Вычисляем :
Предложить исправление Сохранить Отменить
8) Вычисляем:
Предложить исправление Сохранить Отменить
Danger dungeon quest
Game: Perform tasks and rest cool.7 people play!
Play game
9) Проверяем условие:
150>124.7 – условие не выполняется, необходимо увеличить диаметр поперечной арматуры до 8мм и снова сделать проверку
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Варианты заданий для расчета по поперечной силе.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
вариант
Предложить исправление Сохранить Отменить
b
Предложить исправление Сохранить Отменить
h
Предложить исправление Сохранить Отменить
a
Предложить исправление Сохранить Отменить
B
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Арматура
Предложить исправление Сохранить Отменить
Q
Предложить исправление Сохранить Отменить
задание
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
1
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3¯22IIА
Предложить исправление Сохранить Отменить
50
Предложить исправление Сохранить Отменить
Проверить прочность сечения Q≤Q
Предложить исправление Сохранить Отменить
2
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
3.1
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
2¯18IIIА
Предложить исправление Сохранить Отменить
55
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
42
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
2¯25АII
Предложить исправление Сохранить Отменить
65
Предложить исправление Сохранить Отменить
4
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
43
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3¯18АIII
Предложить исправление Сохранить Отменить
60
Предложить исправление Сохранить Отменить
5
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
44
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
2¯22АII
Предложить исправление Сохранить Отменить
70
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
45
Предложить исправление Сохранить Отменить
3.6
Предложить исправление Сохранить Отменить
12.5
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3¯20АIII
Предложить исправление Сохранить Отменить
75
Предложить исправление Сохранить Отменить
7
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
46
Предложить исправление Сохранить Отменить
3.7
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
2¯25АII
Предложить исправление Сохранить Отменить
80
Предложить исправление Сохранить Отменить
8
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
47
Предложить исправление Сохранить Отменить
4.0
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
2¯18АIII
Предложить исправление Сохранить Отменить
85
Предложить исправление Сохранить Отменить
9
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
48
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3¯25АII
Предложить исправление Сохранить Отменить
65
Предложить исправление Сохранить Отменить
10
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
49
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
30
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
2¯20АIII
Предложить исправление Сохранить Отменить
58
Предложить исправление Сохранить Отменить
11
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
50
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
12.5
Предложить исправление Сохранить Отменить
0.95
Предложить исправление Сохранить Отменить
3¯18АII
Предложить исправление Сохранить Отменить
70
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
3.1
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
2¯22АIII
Предложить исправление Сохранить Отменить
65
Предложить исправление Сохранить Отменить
13
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
3.7
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3¯20АII
Предложить исправление Сохранить Отменить
85
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
42
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
2¯18АIII
Предложить исправление Сохранить Отменить
70
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
43
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
30
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3¯25АII
Предложить исправление Сохранить Отменить
75
Предложить исправление Сохранить Отменить
16
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
44
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
2¯20АIII
Предложить исправление Сохранить Отменить
60
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
45
Предложить исправление Сохранить Отменить
3.8
Предложить исправление Сохранить Отменить
12.5
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3¯20АII
Предложить исправление Сохранить Отменить
87
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
46
Предложить исправление Сохранить Отменить
3.9
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
2¯18АIII
Предложить исправление Сохранить Отменить
78
Предложить исправление Сохранить Отменить
19
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
3.8
Предложить исправление Сохранить Отменить
30
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
2¯25АII
Предложить исправление Сохранить Отменить
59
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
4.0
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
0.95
Предложить исправление Сохранить Отменить
3¯18АIII
Предложить исправление Сохранить Отменить
65
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
43
Предложить исправление Сохранить Отменить
3.7
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
2¯20АII
Предложить исправление Сохранить Отменить
64
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
44
Предложить исправление Сохранить Отменить
3.8
Предложить исправление Сохранить Отменить
30
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3¯22АIII
Предложить исправление Сохранить Отменить
60
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
42
Предложить исправление Сохранить Отменить
3.1
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
2¯18АII
Предложить исправление Сохранить Отменить
85
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
50
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
0.95
Предложить исправление Сохранить Отменить
3¯25АII
Предложить исправление Сохранить Отменить
75
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
48
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
12.5
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
2¯20АIII
Предложить исправление Сохранить Отменить
70
Предложить исправление Сохранить Отменить
Danger dungeon quest
Game: Perform tasks and rest cool.7 people play!
Play game
Danger dungeon quest
Game: Perform tasks and rest cool.7 people play!
Play game
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить

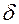 , а поперечная сила Q – касательные напряжения
, а поперечная сила Q – касательные напряжения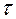 . По наклонным сечениям балки будут действовать главные растягивающие
. По наклонным сечениям балки будут действовать главные растягивающие 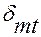 и главные сжимающие напряжения
и главные сжимающие напряжения 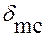 . Когда главные растягивающие напряжения превысят предельные сопротивления бетона растяжению Rbt , в нем появляются наклонные трещины (стадия Ia). Части элемента, находящиеся справа и слева от наклонной трещины, стремятся взаимно повернуться вокруг точки А, расположенной в сжатой зоне сечения над трещиной. Такому повороту препятствует продольная арматура, пересеченная трещиной и работающая на растяжение, поперечная арматура (хомуты) и отгибы.
. Когда главные растягивающие напряжения превысят предельные сопротивления бетона растяжению Rbt , в нем появляются наклонные трещины (стадия Ia). Части элемента, находящиеся справа и слева от наклонной трещины, стремятся взаимно повернуться вокруг точки А, расположенной в сжатой зоне сечения над трещиной. Такому повороту препятствует продольная арматура, пересеченная трещиной и работающая на растяжение, поперечная арматура (хомуты) и отгибы.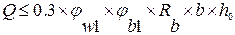 ,(1)
,(1)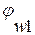 - коэфицент, учитывающий влияние поперечной арматуры
- коэфицент, учитывающий влияние поперечной арматуры  , где
, где 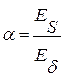 ;
;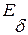 - модуль упругости бетона;
- модуль упругости бетона;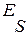 - модуль упругости арматурной стали;
- модуль упругости арматурной стали; ;
;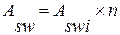 , где
, где 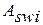 - площадь сечения одного хомута в сечении балки; n- число хомутов в сечении элемента (число стержней арматуры, полученного в результате расчета нормального сечения)
- площадь сечения одного хомута в сечении балки; n- число хомутов в сечении элемента (число стержней арматуры, полученного в результате расчета нормального сечения)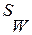 - расстояние между хомутами.
- расстояние между хомутами.
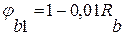 - для тяжелого бетона.
- для тяжелого бетона.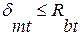 .
.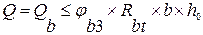 ,(2)
,(2)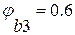 ;
; 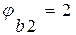 - для тяжелого бетона.
- для тяжелого бетона.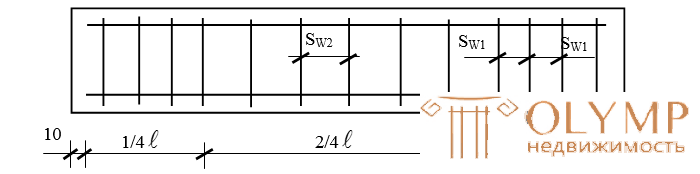
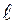 (3)
(3)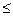 450мм =>
450мм =>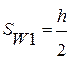 и не >150мм
и не >150мм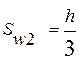 и не > 500мм (4)
и не > 500мм (4)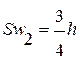 и не >500мм (5)
и не >500мм (5)
 и проводят горизонтальную линию, параллельную оси. Место пересечения этой линии с эпюрой изгибающих моментов (сеч. 1-1) и будет местом теоретического отрыва 2-х стержней.
и проводят горизонтальную линию, параллельную оси. Место пересечения этой линии с эпюрой изгибающих моментов (сеч. 1-1) и будет местом теоретического отрыва 2-х стержней.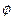 20 AIII
20 AIII
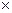 105мПа
105мПа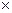 103мПа
103мПа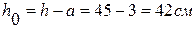
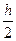 =
=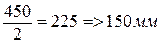
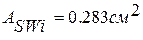
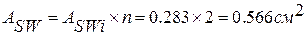
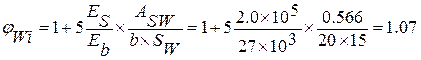
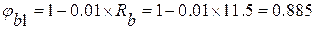 , проверяем условие
, проверяем условие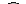
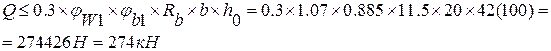 тт.е. наклонные трещины не образуются.
тт.е. наклонные трещины не образуются.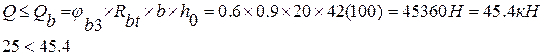
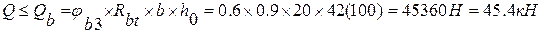
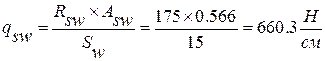
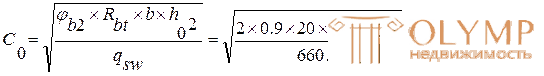
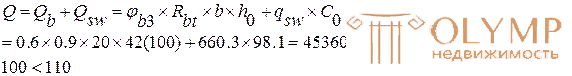
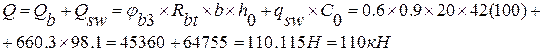
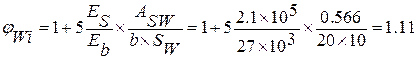
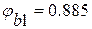
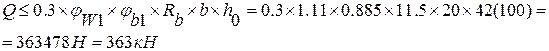
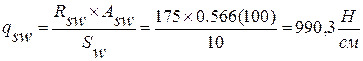
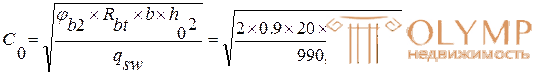
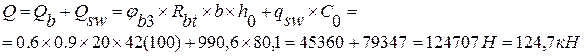 150>124.7 – условие не выполняется, необходимо увеличить диаметр поперечной арматуры до 8мм и снова сделать проверку
150>124.7 – условие не выполняется, необходимо увеличить диаметр поперечной арматуры до 8мм и снова сделать проверку
Что бы оставить комментарий войдите
Комментарии (0)