2.4. The relationship between the directional angles of the previous and subsequent lines

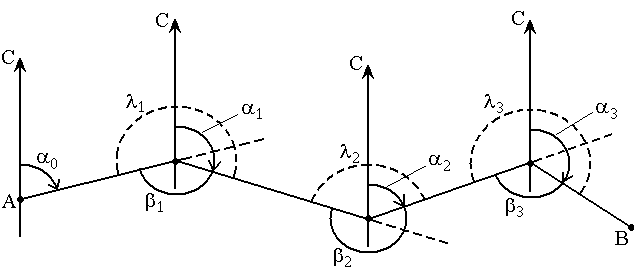
In fig. 25 shows the scheme for determining the directional angles of the sides of the trapline AB . The directional angle of the source side α0 is known and the angles β1, β2, β3 , measured by a theodolite by a geodetic instrument, are angles β1, β2, β3 , which lie to the right from A to B.

Fig. 25. The scheme for determining the directional angles of the sides of the traverse

Find the directional angles α1, α2, α3 of the other sides of the stroke.

Based on the relationship between forward and reverse directional angles, we can write:

α1 + β1 = α0 + 180 ° from this expression, it follows that α1 = α0 + 180 ° - β1 (1) .

The directional angles of the subsequent sides of the traverse are calculated in the same way:

α2 + β2 = α1 + 180 ° → α2 = α1 + 180 ° - β2 (2)

α3 + β3 = α2 + 180 ° → α3 = α2 + 180 ° - β3 (3)

.................................................. .............................

αn + βn = αn-1 + 180 ° → αn = αn-1 + 180 ° - βn (n)

That is, the directional angle of the subsequent side is equal to the directional angle of the previous side plus 180 ° and minus the angle lying to the right along the course.

To obtain the control formula in the expression (2) we substitute the value α1 , from the expression (1)

α2 = α0 + 2 ∙ 180 ° - (β1 + β2) .

If we continue the similar actions for the subsequent parties of the theodolite course, we get

αn = α0 + n ∙ 180 ° - (β1 + β2 + β3 + ... + βn) .

or

αn - α0 = n ∙ 180 ° - ∑β .

or

α0 - αn = ∑β - n ∙ 180 ° .

This formula can serve as a control when calculating the direction angles for the associated angles β .

If instead of the sum of the corrected angles, we substitute the sum of the measured angles ∑β , then the same formula will allow us to determine the discrepancy fβ of the measured angles of the theodolite stroke if the directional angles α0 and αn of the initial and final sides of the stroke

fβ = ∑β - n ∙ 180 ° - (α0 - αn) .

Sometimes the directional angles are calculated from the angles lying to the left along the direction from A to B ( λ1, λ2, ..., λn ).

β1 = 360 ° - λ1

β2 = 360 ° - λ2

........................

βn = 360 ° - λn

Substitute these values ​​into expressions (1) , (2) , ..., (n) we get

α1 = α0 - 180 ° + λ1

α2 = α1 - 180 ° + λ2

.................................

αn = αn-1 - 180 ° + λn   .

To verify the correctness of the calculation of the directional angles of the angles λ , lying to the left along the course, use

αn - α0 = ∑λ - n ∙ 180 °

or

αn - α0 = ∑λ + n ∙ 180 ° .

Then the residual f β is determined by the formula

fβ = ∑λ + n ∙ 180 ° - (αn - α0) .

2.5. Questions for self-control

1. What is terrain orientation?

2. What is the direction angle of the line, and in what limits is it measured?

3. What is the rumba line, and to what extent is it measured?

4. What is called true and magnetic azimuths?

5. What is the relationship between the direction angle and the true azimuth and between the true azimuth and magnetic azimuth?

6. What is called the convergence of the meridians?

7. What is the declination of the magnetic needle?