Главные центральные моменты инерции сложных сечений произвольной формы кратко

При отсутствии у заданного сечения оси симметрии задача решается в следующей порядке последовательности:

1. Сечение разбиваем на простые фигуры и проводим их вертикальные и горизонтальные центральные оси.

2. Проводим произвольные оси Z' и Y', параллельные центральным осям простых фигур.

3. Определяем координаты центра тяжести заданного сечения z_Сиy_Сотносительно осейZ' и Y' по формулам (5.3).

4. Откладываем расстояния z_Сиy_Сс учетом знаков от осейZ' и Y' и проводим центральные оси всего сеченияZиY, параллельные осямZ' и Y'.

5. Определяем осевые и центробежные моменты инерции всего сечения относительно осей ZиYпо формулам (5.9).

6. Определяем величины главных центральных (экстремальных) моментов инерции всего сечения по формуле:

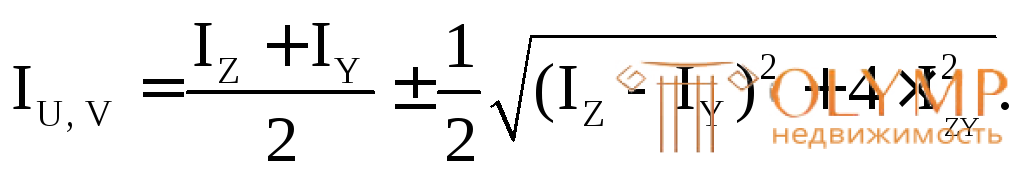(5.21)

7. Определяем положение главных центральных осей:

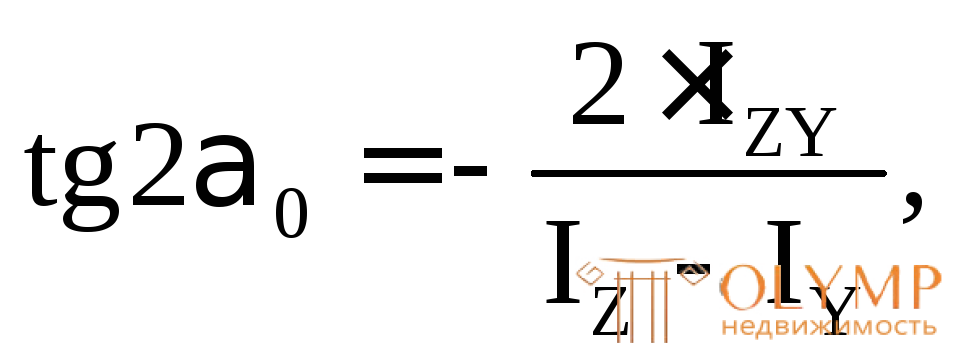(5.22)

где 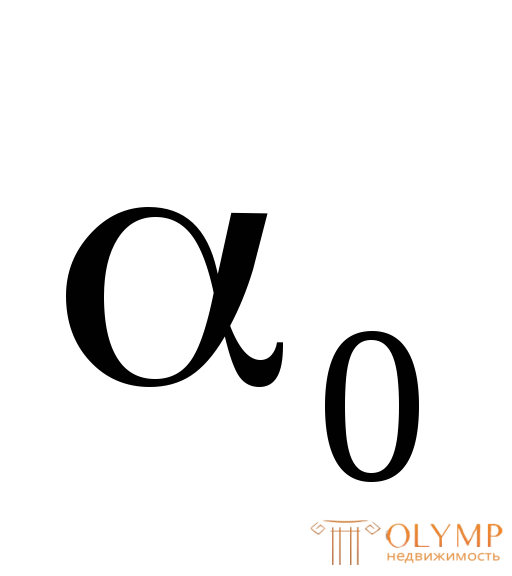– угол, на который нужно повернуть осиZиY, чтобы они стали главными.

Угол 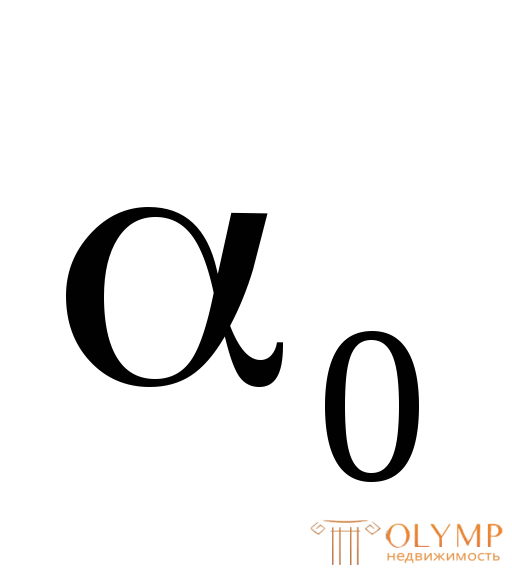нужно отложить против хода часовой стрелки, если он имеет знак "плюс" и по ходу часовой стрелки – если знак "минус".

ПРИМЕР 5.4

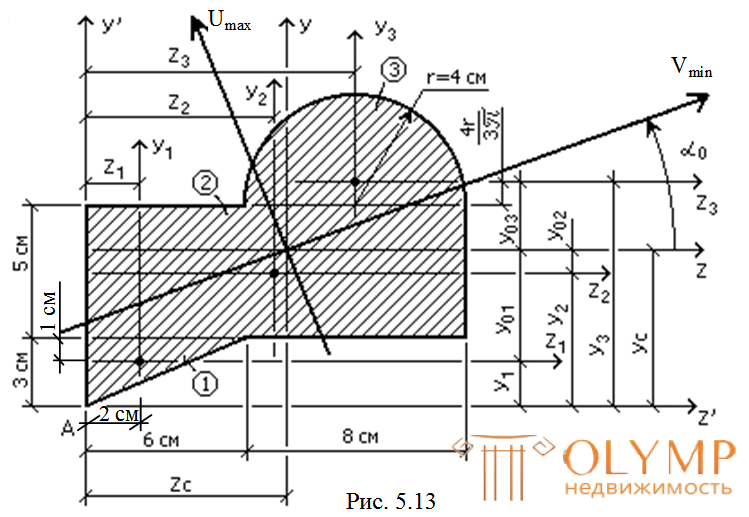
Требуется определить величины главных центральных моментов инерции и положение главных центральных осей инерции для сечения, изображенного на рис. 5.13.

РЕШЕНИЕ

1. Разбиваем сложное сечение на простые фигуры: 1 (треугольник), 2 (прямоугольник), 3 (полукруг).

2. Изобразим вертикальные и горизонтальные центральные оси для этих фигур.

3. Определяем площади и моменты инерции простых фигур относительно их центральных осей (собственные моменты инерции):

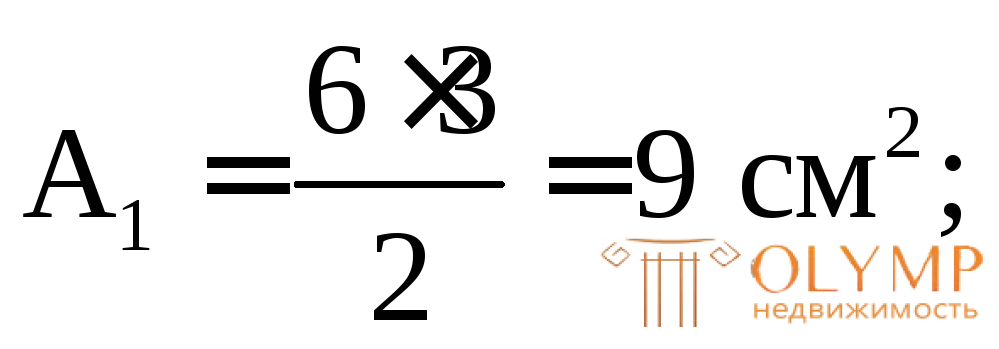
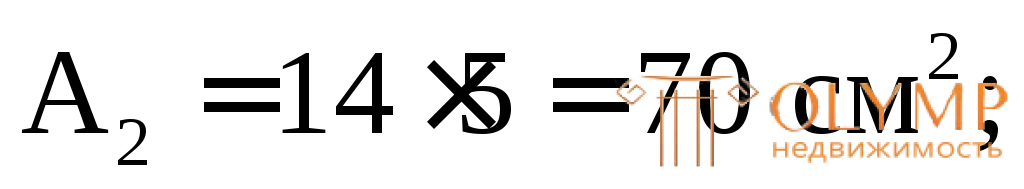
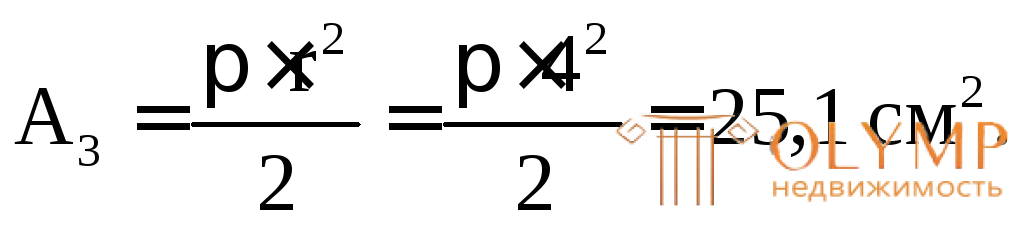
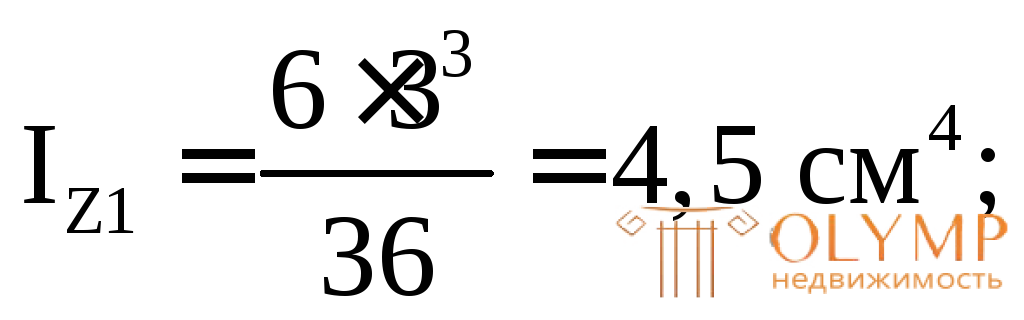
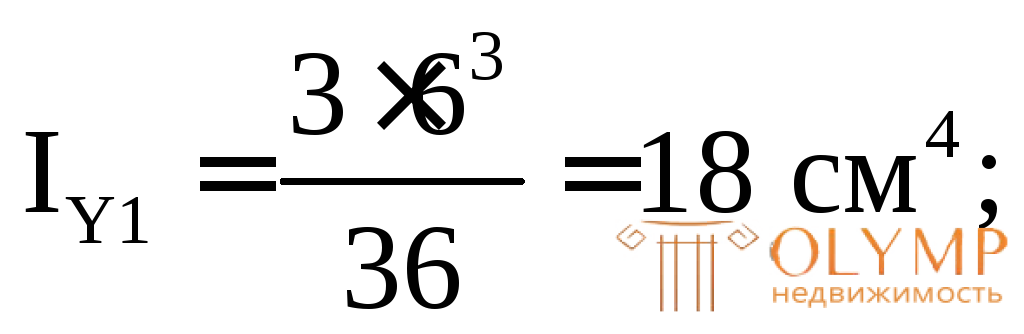
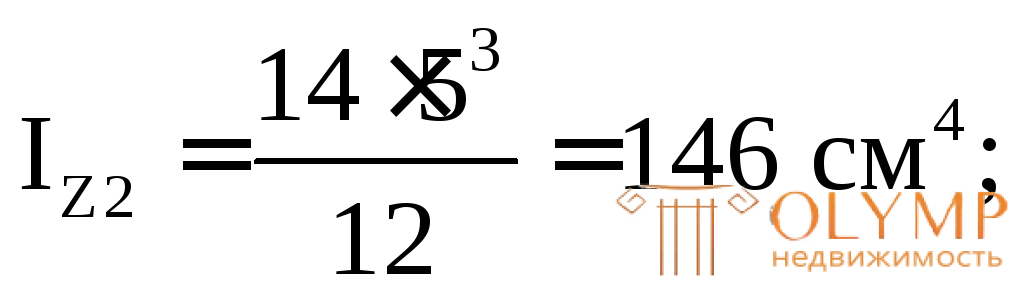
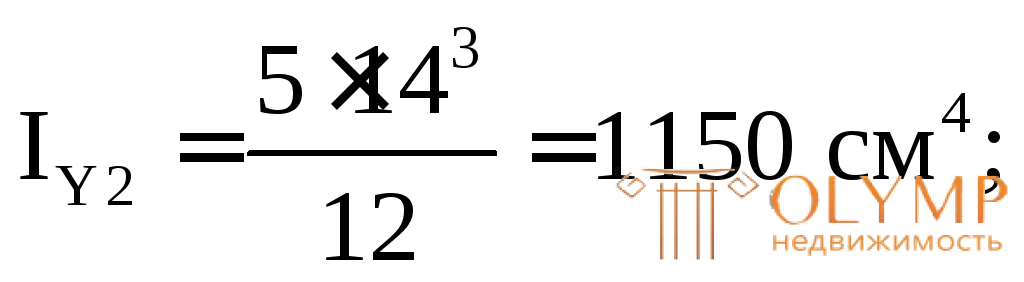
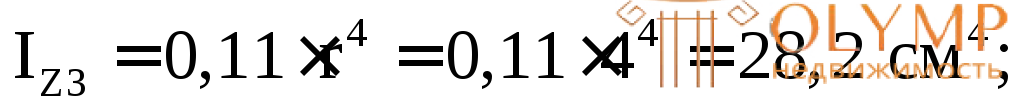
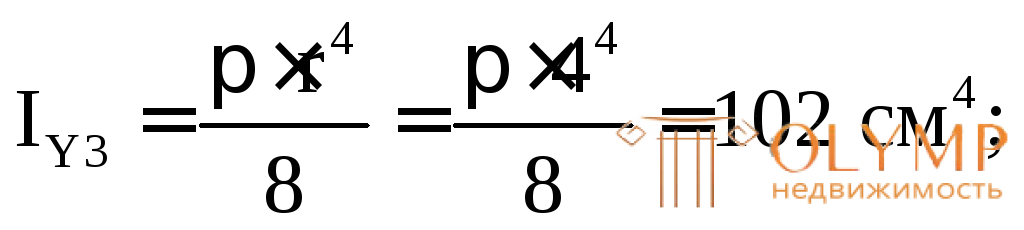
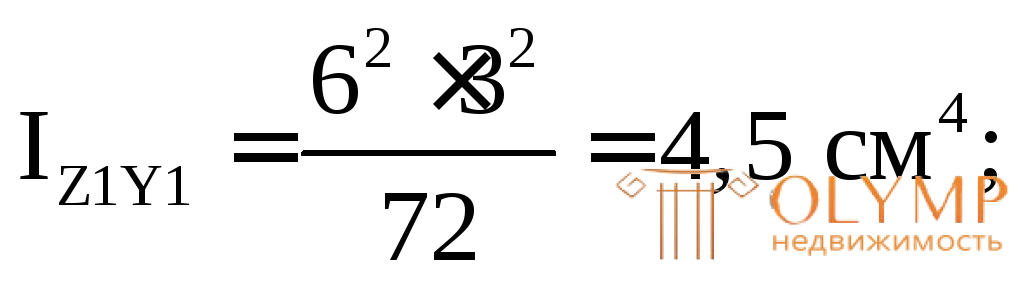
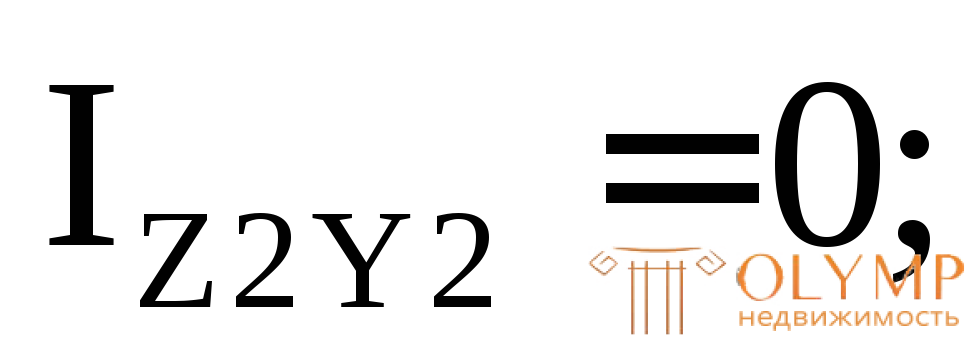
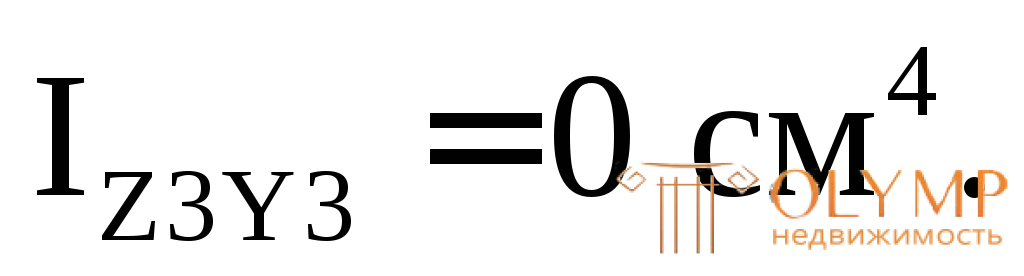
4. Проводим через точку А оси для всего сечения Z' и Y', параллельные центральным осям простых фигур (в данном случае они являются касательными к фигуре снизу и слева).

5. Определяем координаты центра тяжести всего сечения z_Си у_Сотносительно произвольных осейZ' и Y':

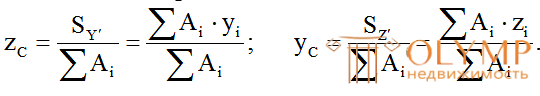
Расстояния 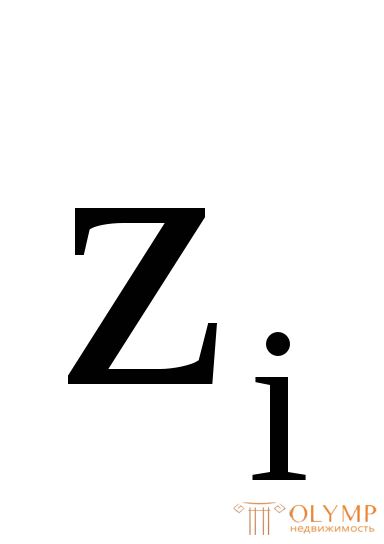и– от произвольно взятых осей Z' и Y' до центральных осей простых фигур показаны на рис. 5.13.

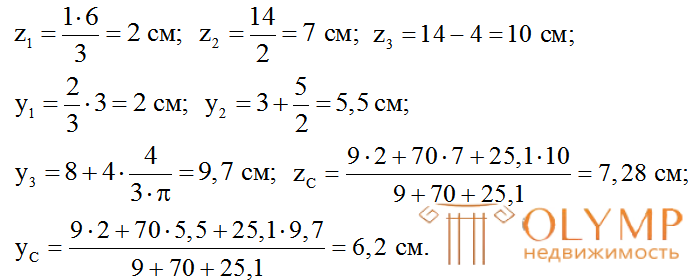
Отложим эти расстояния от осей Z' и Y' и проведем центральные оси для всей фигуры – осиZиY.

6. Расстояния z_0iиy_0iот центральных осей всего сеченияZиYдо центральных осей простых фигурZ_iиY_i:

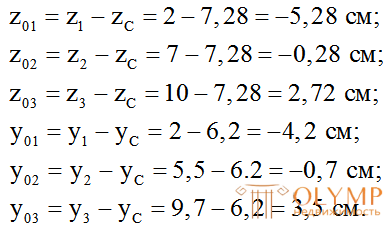
7. Осевые и центробежные моменты инерции сечения относительно общих центральных осей ZиYопределяем по формулам (3.9):

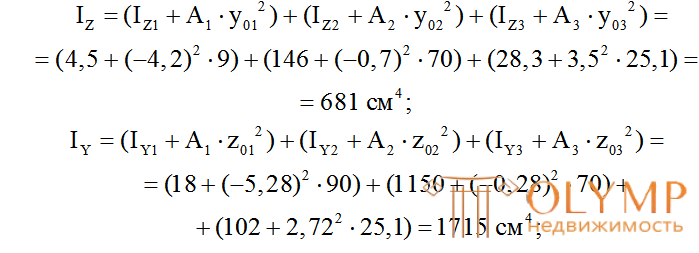
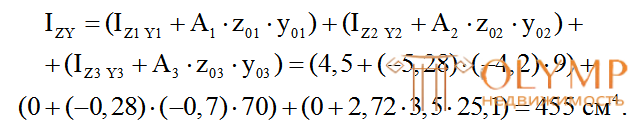
8. Главные центральные моменты инерции сечения:

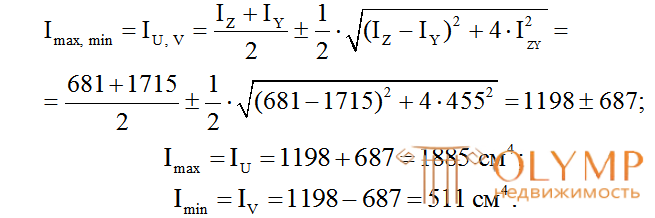
Проверка:

I_Z + I_Y = I_max + I_min

681 + 1715 = 1885 + 511 = 2396 см⁴.

9. Положение главных центральных осей инерции определим по формуле (5.22):

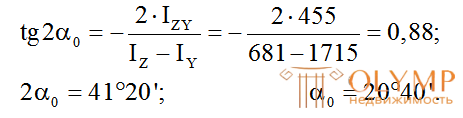
Если 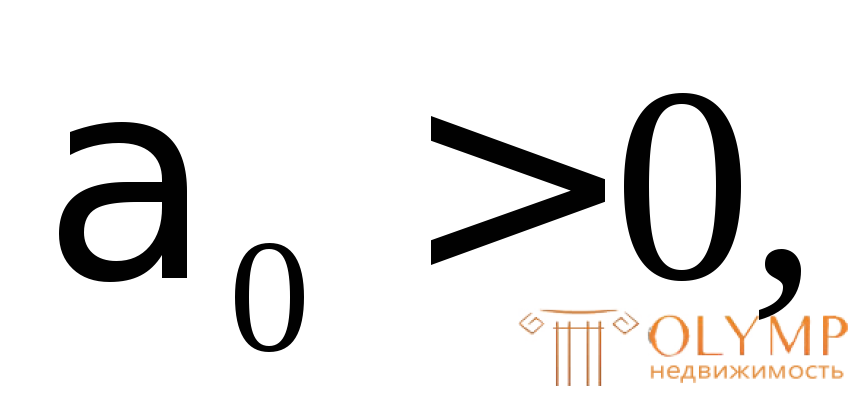значит осиZиYнужно повернуть на угол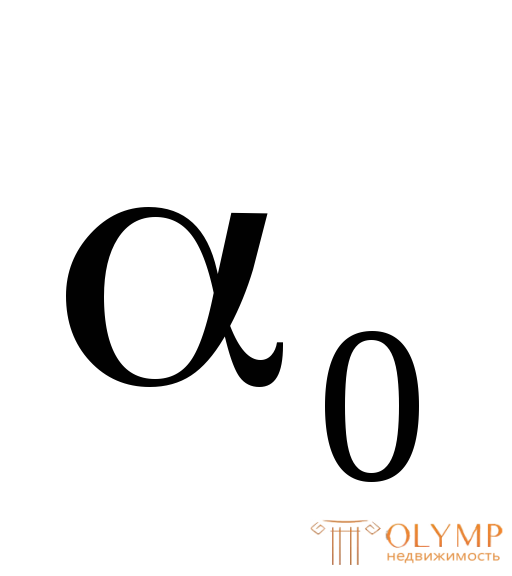против хода часовой стрелки для получения главных центральных осейUиV.

Положение главных центральных осей U_maxиV_minпроверяется по двум, взаимно дополняющим друг друга правилам:

1. Если центробежный момент инерции всей фигуры 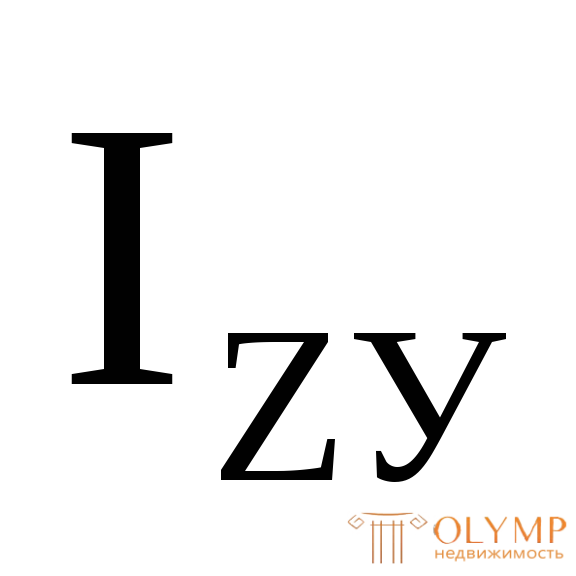положительный, то ось V_min проходит через 1-ю и 3-ю координатные четверти.

2. Ось V_min всегда ближе к той из двух центральных осей ZиY, осевой момент инерции которой меньше.

ПРИМЕР 5.5

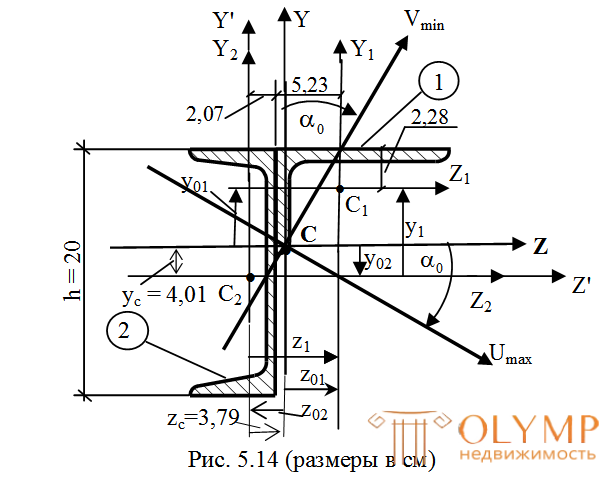
Для составного сечения, изображенного на (рис. 5.14), состоящего из швеллера № 20 и неравнополочного уголка № 16⁄10 (t= 10 мм),требуетсяопределить:

1. Положение центра тяжести сечения.

2. Положение главных центральных осей инерции.

3. Величины главных центральных моментов инерции.

4. Величины главных радиусов инерции сечения.

РЕШЕНИЕ

1. Разбиваем сложное сечение на простые фигуры: 1 (уголок), 2 (швеллер).

2. Проводим центральные оси для этих простых фигур.

3. Выписываем из таблиц сортаментов для неравнополочных уголков (ГОСТ 8510-86) и швеллеров (ГОСТ 8240-89) площади и моменты инерции простых фигур относительно их центральных осей (собственные моменты инерции).

1-я фигура – неравнополочный уголок № 16/10 (t = 10 мм):

Примечания:

1. В зависимости от ориентации уголка по отношению осей Z и Y (рис. 5.15) его центробежный момент инерции может быть положительным или отрицательным. Если минимальная ось инерции уголка проходит через положительные четверти (1- и 3-ю), то собственный центробежный момент инерции уголка будет положительным, а если она проходит через отрицательные четверти (2- и 4-ю) то центробежный момент инерции уголка будет отрицательным (рис 5.15). В данном случае он положительный, так как ось min проходит в положительных четвертях.

2. Расположение большего размера уголка на заданном чертеже не совпадает с его положением на рисунке в таблице сортаментов, поэтому осевые моменты инерции приведены с двойным обозначением.

2-я фигура – швеллер № 20:

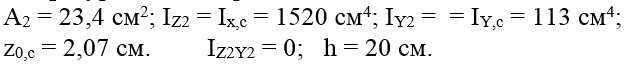
Здесь буквы "с" и "х" в индексах – ссылка на обозначения осей в сортаменте.

4. Проводим через произвольную точку С₂– центр тяжести 2-й фигуры произвольные оси для всего сеченияZ' и Y', совпадающие с осямиZ₂иY₂.

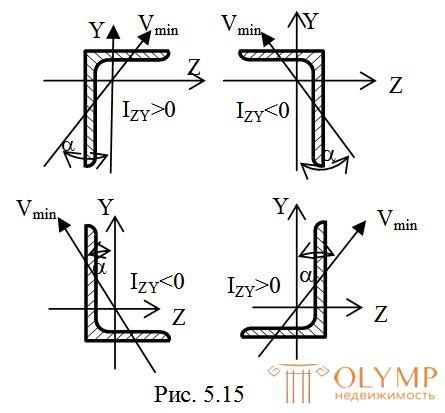
5. Определяем координаты центра тяжести всего сеченияzи уотносительно произвольных осейZ' и Y':

Расстояния и– от произвольно взятых осей Z' и Y' до центральных осей простых фигур показаны на рис. 5.14.

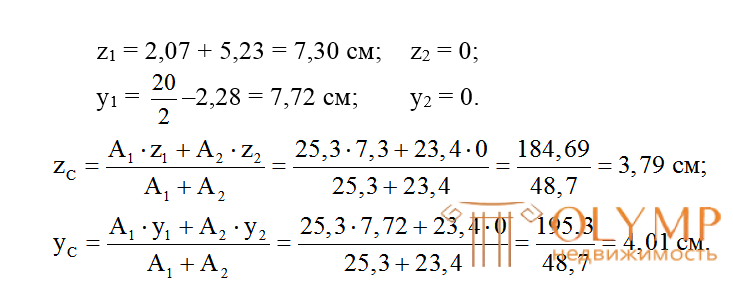
Отложим эти расстояния от осей Z' и Y' и проведем центральные оси для всей фигуры –ZиY. На пересечении этих осей находится точка С – центр тяжести всей площади.

6. Определяем расстоянияz_0i,y_0iот центральных осей всего сеченияZиYдо центральных осей простых фигур:

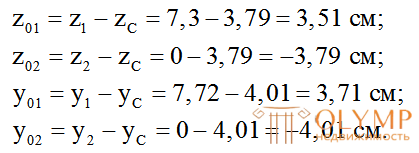
7. Вычисляем осевые и центробежные моменты инерции сечения относительно общих центральных осей ZиYпо формулам (3.9):

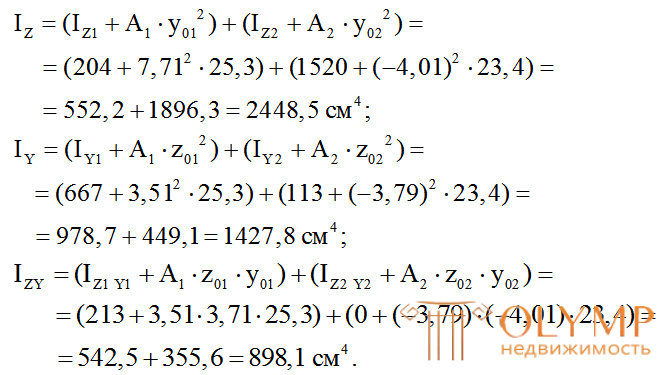
8. Величины главных центральных моментов инерции сечения вычислим по формуле (5.21):

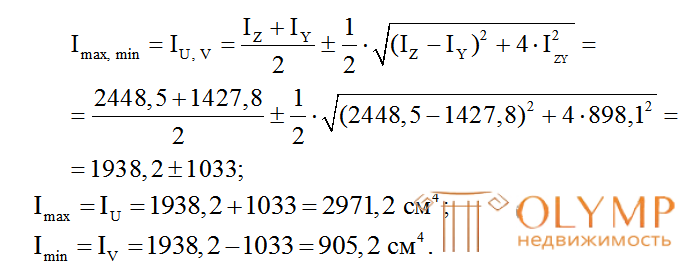
9. Определим положение главных центральных осей инерции по формуле (5.22):

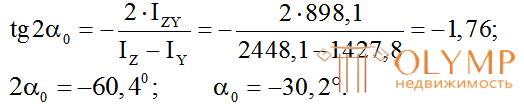
Если α₀< 0, значит, для получения главных центральных осейUиVосиZиYнужно повернуть на угол₀ по ходу часовой стрелки

Выполним проверку: I_Z+I_Y=I_max+I_min;

2448,5 + 1427,8 = 2971 + 905,2 = 3876,2 см⁴.

10. Определим значения главных центральных радиусов инерции сечения.

Радиусом инерции сечения относительно какой-либо оси называется квадратный корень от отношения осевого момента инерции относительно этой оси к площади сечения.

Контрольные вопросы по теме

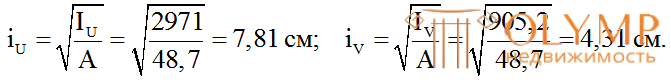
1. Что называется статическим моментом площади относительно оси?

2. Относительно каких осей статический момент площади равен нулю?

3. Как определяется статический момент площади сложной формы относительно оси?

4. Напишите формулы для определения координат центра тяжести сечения сложной формы.

5. Что называется осевым, центробежным и полярным моментами инерции сечения?

6. Относительно каких осей центробежный момент инерции сечения равен нулю?

7. Какие оси называются главными?

8. Приведите формулы для определения моментов инерции наиболее распространенных простых фигур относительно их центральных осей.

9. По каким формулам определяются моменты инерции площадей при параллельном переносе осей?

10. По каким формулам определяются осевые и центробежный моменты инерции сечения сложной формы?

11. Как определяются величины главных центральных моментов инерции для сечений, не имеющих оси симметрии?

12. Как определяется положение главных центральных осей инерции для сечений, не имеющих осей симметрии?

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.