Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
In the first period of the use of reinforced concrete, the overlapping of structures was carried out in the form of solid plates. However, such constructions are not rational, since the height of the compressed zone is 1/10 ... 1/15 of their height, and the stretched zone of the cross-section of concrete is not taken into account in the calculation of strength and serves to accommodate the reinforcement.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
If part of the concrete is removed from the stretched zone, leaving it only near the reinforcing bars, then a ribbed plate will be obtained. The plate carrying capacity will not change, and the consumption of concrete and the weight of the structure will be significantly reduced. Such elements, called Tauri, are widely used in the form of beams, decking, as a part of monolithic ribbed floors.
Предложить исправление Сохранить Отменить
Experience shows that in areas remote from the edge of the voltage will be less. This is taken into account by the conditional decrease in the width of the overhangs entered into the calculation.
Предложить исправление Сохранить Отменить
1) b'f = b + 12h'f npu h'f
Предложить исправление Сохранить Отменить
2) b'f = b + 6h'f at 0.05 h
Предложить исправление Сохранить Отменить
3) b'f = b with h'f <0.05h
Предложить исправление Сохранить Отменить
When calculating T-shaped beams, two cases are distinguished: 1. A compressed section area is within a shelf, or below the shelf
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
CASE 1 (x h f ')
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Case 1 occurs in sections with a developed shelf, when the external bending moment is less than or equal to the internal moment perceived by the compressed section shelf relative to the center of gravity of the reinforcement.
Предложить исправление Сохранить Отменить
T-shaped section of this type is calculated as rectangular with dimensions b'f and h, since the area of the stretched concrete does not affect the bearing capacity. For the calculation, the formulas obtained for rectangular section with single reinforcement are used, in which "b" is replaced with "b'f".
Предложить исправление Сохранить Отменить
l. Rb • b'f • x = Rs • As (1)
Предложить исправление Сохранить Отменить
2. M
Предложить исправление Сохранить Отменить
3. M
Предложить исправление Сохранить Отменить
Selection of a T-section can be made, as for a rectangular section according to tabular data using the formulas:
Предложить исправление Сохранить Отменить
4. A0 = M / Rb • b'f • ho2
Предложить исправление Сохранить Отменить
5. As = M /
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
CASE 2 (x> h'f)
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
The neutral axis extends beyond the shelf and intersects the edge, (x> h'f), i.e. the external design moment will be greater than the internal moment perceived only by the compressed shelf. Tavrovye sections of this type are found in the calculation of beam structures with a small width of the overhangs of the shelf.
Предложить исправление Сохранить Отменить
To obtain the calculated formulas, the bending moment perceived by the section is divided into two points:
Предложить исправление Сохранить Отменить
but). Mfl - perceived by the shelf overhangs and the corresponding Asfl reinforcement.
Предложить исправление Сохранить Отменить
b). Mrib - perceived by the compressed concrete edges and the corresponding reinforcement As.rib.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
The concrete of the overhangs of the flange works for compression, and the tension is the corresponding part of the entire reinforcement As.rib. This section takes the moment:
Предложить исправление Сохранить Отменить
6). Mfl = Nb, fl • z = Rb • (b'f-b) • h'f • (ho - h'f / 2) (6)
Предложить исправление Сохранить Отменить
From the condition of equality "0" the sum of the projections of all forces on the element axis:
Предложить исправление Сохранить Отменить
Nb, fl = Nsfl
Предложить исправление Сохранить Отменить
Rb • (b'f-b) • h'f = Rs • As fl, from where
Предложить исправление Сохранить Отменить
7). As fl = Rb • (b'f-b) • h'f / Rs (7)
Предложить исправление Сохранить Отменить
This reinforcement constitutes only a part of the complete reinforcement As, now we will find the rest of the reinforcement corresponding to the reinforcement of the rib As.rib.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
The rib concrete is working in compression at the height of the compressed zone x, and in tension the rest of the entire tensile reinforcement As.rib.
Предложить исправление Сохранить Отменить
The stress state of this scheme is fully consistent with the stress state of a rectangular section with a height of "h" and a width of "b" with a single reinforcement, which perceives the moment:
Предложить исправление Сохранить Отменить
eight). Mrib = M- Mfl (8)
Предложить исправление Сохранить Отменить
The area of the As.rib reinforcement is defined as for a rectangular section with a single reinforcement width “b”:
Предложить исправление Сохранить Отменить
9). A0 = Mrib / Rb • b • ho2
Предложить исправление Сохранить Отменить
10. As rib = Mrib /
Предложить исправление Сохранить Отменить
The total cross section of tensile reinforcement is determined by the formula:
Предложить исправление Сохранить Отменить
eleven). As = As fl + As.rib (11)
Предложить исправление Сохранить Отменить
Further, according to table 7 of the application, we find the diameter and the number of longitudinal bars required for the reinforcement of the beam.
Предложить исправление Сохранить Отменить
When calculating T-sections, determine which design case (x
Предложить исправление Сохранить Отменить
find the boundary moment MX = h'f = Rb • b'f • h'f • (ho - h'f / 2) (12)
Предложить исправление Сохранить Отменить
If the current moment from external forces M
Предложить исправление Сохранить Отменить
When calculating T-sections, it is most often necessary to solve the problem of determining the cross-sectional area of As reinforcement for given section sizes, material classes and the calculated bending moment "M"
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Decision plan.
Предложить исправление Сохранить Отменить
1. Set the estimated width of the shelf b'f.
Предложить исправление Сохранить Отменить
2. According to the formula (12), calculate Мh = h'f and determine which calculation case the section relates to;
Предложить исправление Сохранить Отменить
3. Find the cross-sectional area of the armature As:
Предложить исправление Сохранить Отменить
3.1 at (x
Предложить исправление Сохранить Отменить
3.2 when (x> h'f) - first determine Mfl by the formula (6) and As fl
Предложить исправление Сохранить Отменить
according to the formula (7). Then Mrib is determined by the formula (8) and As rib by the formula (10), as for a rectangular beam with the width "b". The total cross section of tensile reinforcement is found by the formula (11).
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Type 2 Task
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
If you want to establish the carrying capacity of a given section of the formula (1) determine the height of the compressed zone:
Предложить исправление Сохранить Отменить
X = Rs • As / Rb • b'f
Предложить исправление Сохранить Отменить
If (x
Предложить исправление Сохранить Отменить
according to formula 2:
Предложить исправление Сохранить Отменить
M
Предложить исправление Сохранить Отменить
If x> h'f, then the calculation procedure is as follows:
Предложить исправление Сохранить Отменить
1. Determine As, fl no by the formula (7) and Mfl by the formula 6.
Предложить исправление Сохранить Отменить
2. Find As, rib from formula 11
Предложить исправление Сохранить Отменить
3. Count Mrib, as for a rectangular section with
Предложить исправление Сохранить Отменить
single valve:
Предложить исправление Сохранить Отменить
first determine:
Предложить исправление Сохранить Отменить
x = Rs • As, rib / Rb • b, and then:
Предложить исправление Сохранить Отменить
4. Mrib = Rs • As, rib (ho - x / 2)
Предложить исправление Сохранить Отменить
5. Determine the total moment perceived by the section (its carrying capacity):
Предложить исправление Сохранить Отменить
M = Mfl + Mrib
Предложить исправление Сохранить Отменить
EXAMPLE N1
Предложить исправление Сохранить Отменить
Determine the area of As reinforcement in the element of the T-section according to the following data:
Предложить исправление Сохранить Отменить
M = 42 kNm;
Предложить исправление Сохранить Отменить
Armature class A111
Предложить исправление Сохранить Отменить
Concrete B15;
Предложить исправление Сохранить Отменить
b'f = 80cm; Yi = 1
Предложить исправление Сохранить Отменить
h = 40 cm; h'f = 4 cm;
Предложить исправление Сохранить Отменить
b = 14 cm
Предложить исправление Сохранить Отменить
a = 3cm
Предложить исправление Сохранить Отменить
Decision.
Предложить исправление Сохранить Отменить
According to the tables of the application, we determine the calculated characteristics:
Предложить исправление Сохранить Отменить
Rb = 8.5 • 1 = 8.5mPa; Rs = 365mPa
Предложить исправление Сохранить Отменить
To determine the estimated width of the flange, we find the ratio h'f / h = 4/40 = 0.1– taken b'f = b + 12h'f = 14 + 12 • 4 = 62cm
Предложить исправление Сохранить Отменить
1). Find the useful (working) section height ho = h-a = 40-3 = 37cm
Предложить исправление Сохранить Отменить
2). We calculate the boundary moment Мх = h'f = Rb • b'f • h'f • (ho - h'f / 2) (100) =
Предложить исправление Сохранить Отменить
8.5 • 62 • 4 • (37-4 / 2) • (100) = 7378000nsm = 73.8kNm> 42 kNm, therefore, we have the 1st calculation case.
Предложить исправление Сохранить Отменить
We define As as for a rectangular section of width b'f
Предложить исправление Сохранить Отменить
3) .A0 = M / Rb • b'f • ho2
Предложить исправление Сохранить Отменить
A0 = 42 • 105 / 8.5 • 62 • 372 • (100) = 0.058 <Aomax = 0.42 (tab.5 of the appendix)
Предложить исправление Сохранить Отменить
By A0 we define
Предложить исправление Сохранить Отменить
4). Find As = M /
Предложить исправление Сохранить Отменить
According to table 7 of the application we take 3¯12АIII with As, fact = 3.39 cm2
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
EXAMPLE N2
Предложить исправление Сохранить Отменить
According to the previous example, determine As if M = 86 kNm.
Предложить исправление Сохранить Отменить
Decision.
Предложить исправление Сохранить Отменить
Set the settlement case:
Предложить исправление Сохранить Отменить
Since M> MX = h'f (86> 73.8), we have 2 cases (x> h'f)
Предложить исправление Сохранить Отменить
1). Determine:
Предложить исправление Сохранить Отменить
Mfl = Rb • (b'f-b) • h'f • (ho-h'f / 2) = 8.5 • (62-14) • 4 • (37-4 / 2) (100) = 5712000Nsm = 57.1kNm
Предложить исправление Сохранить Отменить
2). We determine As fl = Rb • (b'f-b) • h'f / Rs = 57.1 • 105/365 • (37-4 / 2) (100) = 4.46 cm2
Предложить исправление Сохранить Отменить
3). We calculate Mrib = M- Mfl = 86-57.1 = 29 kNm
Предложить исправление Сохранить Отменить
4). We calculate A0 = Mrib / Rb • b • ho2
Предложить исправление Сохранить Отменить
A0 = 29 • 105 / 8.5 • 14 • 372 (100) = 0.172 <Aomax;
Предложить исправление Сохранить Отменить
5) .As rib = Mrib /
Предложить исправление Сохранить Отменить
6). We calculate As = As fl + As.rib = 4.46 + 2.39 = 6.85 cm2
Предложить исправление Сохранить Отменить
According to table 7 of the application we take 4¯16АIII with As, fact = 8.04 cm2
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
T-section reinforcement
Предложить исправление Сохранить Отменить
Given: 2¯ 22 ASH L = 7.8m
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Product brand
Предложить исправление Сохранить Отменить
Item Position
Предложить исправление Сохранить Отменить
Name
Предложить исправление Сохранить Отменить
Qty
Предложить исправление Сохранить Отменить
Mass 1det. (kg.)
Предложить исправление Сохранить Отменить
Product weight
Предложить исправление Сохранить Отменить
CR2
Предложить исправление Сохранить Отменить
one
Предложить исправление Сохранить Отменить
¯10АIII L = 1940
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
1.2
Предложить исправление Сохранить Отменить
5.88
Предложить исправление Сохранить Отменить
2
Предложить исправление Сохранить Отменить
¯3ВР1 L = 980
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
0.054
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Product brand
Предложить исправление Сохранить Отменить
Item Position
Предложить исправление Сохранить Отменить
Name
Предложить исправление Сохранить Отменить
Qty
Предложить исправление Сохранить Отменить
Mass 1det. (kg.)
Предложить исправление Сохранить Отменить
Product weight
Предложить исправление Сохранить Отменить
KP1
Предложить исправление Сохранить Отменить
one
Предложить исправление Сохранить Отменить
0 22 AIII / = 7780
Предложить исправление Сохранить Отменить
one
Предложить исправление Сохранить Отменить
23.2
Предложить исправление Сохранить Отменить
34.15
Предложить исправление Сохранить Отменить
2
Предложить исправление Сохранить Отменить
0 10A1 / = 7780
Предложить исправление Сохранить Отменить
one
Предложить исправление Сохранить Отменить
4.8
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
08A1 / = 38O
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
0.15
Предложить исправление Сохранить Отменить
Position
Предложить исправление Сохранить Отменить
Designation
Предложить исправление Сохранить Отменить
Name
Предложить исправление Сохранить Отменить
Count
Предложить исправление Сохранить Отменить
Note
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Assembly units
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
one
Предложить исправление Сохранить Отменить
KPSK 2902 C-32 OSI KR-1
Предложить исправление Сохранить Отменить
skeleton flat KR-1
Предложить исправление Сохранить Отменить
2
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
2
Предложить исправление Сохранить Отменить
KR-2
Предложить исправление Сохранить Отменить
skeleton flat KR-2
Предложить исправление Сохранить Отменить
2
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Details
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
0UA1 / = 18O
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
0.111
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Materials
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Concrete B20
Предложить исправление Сохранить Отменить
m3
Предложить исправление Сохранить Отменить
1.17
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Steel consumption statement
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Brand of elements.
Предложить исправление Сохранить Отменить
Reinforcement products
Предложить исправление Сохранить Отменить
Total
Предложить исправление Сохранить Отменить
Armature class
Предложить исправление Сохранить Отменить
Armature class
Предложить исправление Сохранить Отменить
Armature class
Предложить исправление Сохранить Отменить
82,84
Предложить исправление Сохранить Отменить
B1
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
AI
Предложить исправление Сохранить Отменить
BP1
Предложить исправление Сохранить Отменить
GOST 5781-82
Предложить исправление Сохранить Отменить
GOST 5781-82
Предложить исправление Сохранить Отменить
GOST 5781-82
Предложить исправление Сохранить Отменить
022
Предложить исправление Сохранить Отменить
010
Предложить исправление Сохранить Отменить
Total
Предложить исправление Сохранить Отменить
010
Предложить исправление Сохранить Отменить
08
Предложить исправление Сохранить Отменить
Total
Предложить исправление Сохранить Отменить
03
Предложить исправление Сохранить Отменить
Total
Предложить исправление Сохранить Отменить
46.4
Предложить исправление Сохранить Отменить
9.6
Предложить исправление Сохранить Отменить
56
Предложить исправление Сохранить Отменить
12.38
Предложить исправление Сохранить Отменить
12.3
Предложить исправление Сохранить Отменить
24.68
Предложить исправление Сохранить Отменить
2.16
Предложить исправление Сохранить Отменить
2.16
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Questions for self-monitoring on the topic :
Предложить исправление Сохранить Отменить
"The calculation of the bent elements of the T-section"
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
1. What is the advantage of T-shaped sections over rectangular?
Предложить исправление Сохранить Отменить
2. How many cases are there for calculating T-sections?
Предложить исправление Сохранить Отменить
3. How to determine the case of calculating the T-section?
Предложить исправление Сохранить Отменить
4. What is the boundary moment?
Предложить исправление Сохранить Отменить
5. What is the difference between reinforcing a T-section and a rectangular section?
Предложить исправление Сохранить Отменить
6. What are the KR-2 frameworks for in beams of T-section?
Предложить исправление Сохранить Отменить
7. How to determine the diameter and spacing of transverse reinforcement in the frame of the beam?
Предложить исправление Сохранить Отменить
8. Name the types of reinforcement according to the nature of work in the frame of the beam.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Table 1
Предложить исправление Сохранить Отменить
Design concrete resistance for limiting states of the first group of Rb and Rbt MPa depending on the class of concrete in compressive strength
Предложить исправление Сохранить Отменить
Kind of resistance
Предложить исправление Сохранить Отменить
Concrete
Предложить исправление Сохранить Отменить
Concrete compressive strength class
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
B12.5
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
B 25
Предложить исправление Сохранить Отменить
VZO
Предложить исправление Сохранить Отменить
B 35
Предложить исправление Сохранить Отменить
B40
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Compression oseeoe (prismatic strength) Rb
Предложить исправление Сохранить Отменить
Heavy had a grained
Предложить исправление Сохранить Отменить
7.5
Предложить исправление Сохранить Отменить
8.5
Предложить исправление Сохранить Отменить
11.5
Предложить исправление Сохранить Отменить
14.5
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
19.5
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Axial stretch Rbt
Предложить исправление Сохранить Отменить
Heavy
Предложить исправление Сохранить Отменить
0.6
Предложить исправление Сохранить Отменить
0.75
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
1.05
Предложить исправление Сохранить Отменить
1.2
Предложить исправление Сохранить Отменить
1.3
Предложить исправление Сохранить Отменить
1.4
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
table 2
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Calculated resistance fittings for group I of limit states Rs, MPa
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Stretched
Предложить исправление Сохранить Отменить
Compressed rsc
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Type and grade of steel;
Предложить исправление Сохранить Отменить
longitudinal, transverse (clamps and limb) for bending on an inclined section. Rs
Предложить исправление Сохранить Отменить
transverse (clamps and bends) in the calculation of the transverse force
Предложить исправление Сохранить Отменить
Rsw
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Hot rolled round grade A- I
Предложить исправление Сохранить Отменить
225
Предложить исправление Сохранить Отменить
175
Предложить исправление Сохранить Отменить
225
Предложить исправление Сохранить Отменить
: '
Предложить исправление Сохранить Отменить
Hot rolled periodic
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
class profile:
Предложить исправление Сохранить Отменить
A-ll
Предложить исправление Сохранить Отменить
280
Предложить исправление Сохранить Отменить
225
Предложить исправление Сохранить Отменить
280
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
A-III d-8 mm
Предложить исправление Сохранить Отменить
355
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
285
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
355
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
A-III d- 10. ..40 mm |
Предложить исправление Сохранить Отменить
365
Предложить исправление Сохранить Отменить
290
Предложить исправление Сохранить Отменить
365
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Wire reinforcing periodic profile
Предложить исправление Сохранить Отменить
class bp-i
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
.
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
d, mm:
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
375
Предложить исправление Сохранить Отменить
270
Предложить исправление Сохранить Отменить
375
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
370
Предложить исправление Сохранить Отменить
265
Предложить исправление Сохранить Отменить
365
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
five
Предложить исправление Сохранить Отменить
360
Предложить исправление Сохранить Отменить
260
Предложить исправление Сохранить Отменить
360
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
table 3
Предложить исправление Сохранить Отменить
The ratio between the diameters of the welded rods
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
The diameters of the rods in one direction d1 (mm)
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
five
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
eight
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
sixteen
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
28
Предложить исправление Сохранить Отменить
32
Предложить исправление Сохранить Отменить
36
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
The smallest allowable diameters of rods in a different direction d2 (mm)
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
five
Предложить исправление Сохранить Отменить
five
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
eight
Предложить исправление Сохранить Отменить
eight
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
table 4
Предложить исправление Сохранить Отменить
The modulus of elasticity of reinforcing steel Es
Предложить исправление Сохранить Отменить
Type and grade of steel
Предложить исправление Сохранить Отменить
The modulus of elasticity of reinforcement Es.MPa
Предложить исправление Сохранить Отменить
Core steel AI and A-II
Предложить исправление Сохранить Отменить
210,000
Предложить исправление Сохранить Отменить
A-IIIb
Предложить исправление Сохранить Отменить
200,000
Предложить исправление Сохранить Отменить
A-IV, A-VI, AT-IIIC
Предложить исправление Сохранить Отменить
190,000
Предложить исправление Сохранить Отменить
Reinforcing Wire
Предложить исправление Сохранить Отменить
B-II, BP-II,
Предложить исправление Сохранить Отменить
BP-I
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
200,000
Предложить исправление Сохранить Отменить
170,000
Предложить исправление Сохранить Отменить
Reinforcement ropes
Предложить исправление Сохранить Отменить
K-7, K-19
Предложить исправление Сохранить Отменить
180,000
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
table 5
Предложить исправление Сохранить Отменить
Table: Values
Предложить исправление Сохранить Отменить
Reinforcement class
Предложить исправление Сохранить Отменить
Coefficient
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
VZO
Предложить исправление Сохранить Отменить
B40
Предложить исправление Сохранить Отменить
B50
Предложить исправление Сохранить Отменить
B60
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
AI
Предложить исправление Сохранить Отменить
at
Предложить исправление Сохранить Отменить
0.65
Предложить исправление Сохранить Отменить
0.59
Предложить исправление Сохранить Отменить
0.55
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
AOmax
Предложить исправление Сохранить Отменить
0.48
Предложить исправление Сохранить Отменить
0.42
Предложить исправление Сохранить Отменить
0.4
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
AP
Предложить исправление Сохранить Отменить
at
Предложить исправление Сохранить Отменить
0.62
Предложить исправление Сохранить Отменить
0.57
Предложить исправление Сохранить Отменить
0.52
Предложить исправление Сохранить Отменить
0.47
Предложить исправление Сохранить Отменить
0.44
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
AOmax
Предложить исправление Сохранить Отменить
0.43
Предложить исправление Сохранить Отменить
0.41
Предложить исправление Сохранить Отменить
0.38
Предложить исправление Сохранить Отменить
0.36
Предложить исправление Сохранить Отменить
0.34
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
A-III with ¯
Предложить исправление Сохранить Отменить
6-8 mm
Предложить исправление Сохранить Отменить
at
Предложить исправление Сохранить Отменить
0.59
Предложить исправление Сохранить Отменить
0.54
Предложить исправление Сохранить Отменить
0.5
Предложить исправление Сохранить Отменить
0.44
Предложить исправление Сохранить Отменить
0.41
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
AOmax
Предложить исправление Сохранить Отменить
0.42
Предложить исправление Сохранить Отменить
0.39
Предложить исправление Сохранить Отменить
0.37
Предложить исправление Сохранить Отменить
0.34
Предложить исправление Сохранить Отменить
0.33
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
table 6
Предложить исправление Сохранить Отменить
Coefficient values
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
AO
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
AO
Предложить исправление Сохранить Отменить
0.41
Предложить исправление Сохранить Отменить
0.795
Предложить исправление Сохранить Отменить
0.326
Предложить исправление Сохранить Отменить
0.57
Предложить исправление Сохранить Отменить
0.715
Предложить исправление Сохранить Отменить
0.408
Предложить исправление Сохранить Отменить
0.42
Предложить исправление Сохранить Отменить
0.79
Предложить исправление Сохранить Отменить
0.332
Предложить исправление Сохранить Отменить
0.58
Предложить исправление Сохранить Отменить
0.71
Предложить исправление Сохранить Отменить
0.412
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
0.59
Предложить исправление Сохранить Отменить
0.705
Предложить исправление Сохранить Отменить
0.416
Предложить исправление Сохранить Отменить
0.43
Предложить исправление Сохранить Отменить
0.785
Предложить исправление Сохранить Отменить
0.337
Предложить исправление Сохранить Отменить
0.6
Предложить исправление Сохранить Отменить
0.7
Предложить исправление Сохранить Отменить
0.42
Предложить исправление Сохранить Отменить
0.44
Предложить исправление Сохранить Отменить
0.78
Предложить исправление Сохранить Отменить
0.343
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
0.45
Предложить исправление Сохранить Отменить
0.775
Предложить исправление Сохранить Отменить
0.349
Предложить исправление Сохранить Отменить
0.61
Предложить исправление Сохранить Отменить
0.695
Предложить исправление Сохранить Отменить
0.424
Предложить исправление Сохранить Отменить
0.46
Предложить исправление Сохранить Отменить
0.77
Предложить исправление Сохранить Отменить
0.354
Предложить исправление Сохранить Отменить
0.62
Предложить исправление Сохранить Отменить
0,69
Предложить исправление Сохранить Отменить
0.428
Предложить исправление Сохранить Отменить
0.47
Предложить исправление Сохранить Отменить
0.765
Предложить исправление Сохранить Отменить
0.359
Предложить исправление Сохранить Отменить
0.63
Предложить исправление Сохранить Отменить
0.685
Предложить исправление Сохранить Отменить
0.432
Предложить исправление Сохранить Отменить
0.48
Предложить исправление Сохранить Отменить
0.76
Предложить исправление Сохранить Отменить
0.365
Предложить исправление Сохранить Отменить
0.64
Предложить исправление Сохранить Отменить
0.68
Предложить исправление Сохранить Отменить
0.435
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
0.65
Предложить исправление Сохранить Отменить
0.675
Предложить исправление Сохранить Отменить
0.439
Предложить исправление Сохранить Отменить
0.49
Предложить исправление Сохранить Отменить
0.755
Предложить исправление Сохранить Отменить
0.37
Предложить исправление Сохранить Отменить
0.66
Предложить исправление Сохранить Отменить
0.672
Предложить исправление Сохранить Отменить
0.442
Предложить исправление Сохранить Отменить
0.5
Предложить исправление Сохранить Отменить
0.75
Предложить исправление Сохранить Отменить
0.375
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
0.51
Предложить исправление Сохранить Отменить
0.745
Предложить исправление Сохранить Отменить
0.38
Предложить исправление Сохранить Отменить
0.67
Предложить исправление Сохранить Отменить
0.665
Предложить исправление Сохранить Отменить
0.446
Предложить исправление Сохранить Отменить
0.52
Предложить исправление Сохранить Отменить
0.74
Предложить исправление Сохранить Отменить
0.385
Предложить исправление Сохранить Отменить
0.68
Предложить исправление Сохранить Отменить
0.66
Предложить исправление Сохранить Отменить
0.449
Предложить исправление Сохранить Отменить
0.53
Предложить исправление Сохранить Отменить
0.735
Предложить исправление Сохранить Отменить
0.39
Предложить исправление Сохранить Отменить
0,69
Предложить исправление Сохранить Отменить
0.655
Предложить исправление Сохранить Отменить
0.452
Предложить исправление Сохранить Отменить
0.54
Предложить исправление Сохранить Отменить
0.73
Предложить исправление Сохранить Отменить
0.394
Предложить исправление Сохранить Отменить
0.7
Предложить исправление Сохранить Отменить
0.65
Предложить исправление Сохранить Отменить
0.455
Предложить исправление Сохранить Отменить
0.55
Предложить исправление Сохранить Отменить
0.725
Предложить исправление Сохранить Отменить
0.399
Предложить исправление Сохранить Отменить
_
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
0.56
Предложить исправление Сохранить Отменить
0.72
Предложить исправление Сохранить Отменить
0.403
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
0.01
Предложить исправление Сохранить Отменить
0.995
Предложить исправление Сохранить Отменить
0.01
Предложить исправление Сохранить Отменить
0.21
Предложить исправление Сохранить Отменить
0.895
Предложить исправление Сохранить Отменить
0.188
Предложить исправление Сохранить Отменить
0.02
Предложить исправление Сохранить Отменить
0.99
Предложить исправление Сохранить Отменить
0.02
Предложить исправление Сохранить Отменить
0.22
Предложить исправление Сохранить Отменить
0.89
Предложить исправление Сохранить Отменить
0.196
Предложить исправление Сохранить Отменить
0.03
Предложить исправление Сохранить Отменить
0.985
Предложить исправление Сохранить Отменить
0.03
Предложить исправление Сохранить Отменить
0.23
Предложить исправление Сохранить Отменить
0.885
Предложить исправление Сохранить Отменить
0.203
Предложить исправление Сохранить Отменить
0.04
Предложить исправление Сохранить Отменить
0.98
Предложить исправление Сохранить Отменить
0.039
Предложить исправление Сохранить Отменить
0.24
Предложить исправление Сохранить Отменить
0.88
Предложить исправление Сохранить Отменить
0.211
Предложить исправление Сохранить Отменить
0.05
Предложить исправление Сохранить Отменить
0.975
Предложить исправление Сохранить Отменить
0.048
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
0.06
Предложить исправление Сохранить Отменить
0.97
Предложить исправление Сохранить Отменить
0.058
Предложить исправление Сохранить Отменить
0.25
Предложить исправление Сохранить Отменить
0.875
Предложить исправление Сохранить Отменить
0.219
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
0.26
Предложить исправление Сохранить Отменить
0.87
Предложить исправление Сохранить Отменить
0,226
Предложить исправление Сохранить Отменить
0.07
Предложить исправление Сохранить Отменить
0.965
Предложить исправление Сохранить Отменить
0.067
Предложить исправление Сохранить Отменить
0.27
Предложить исправление Сохранить Отменить
0.865
Предложить исправление Сохранить Отменить
0.236
Предложить исправление Сохранить Отменить
0.08
Предложить исправление Сохранить Отменить
0.96
Предложить исправление Сохранить Отменить
0.077
Предложить исправление Сохранить Отменить
0.28
Предложить исправление Сохранить Отменить
0.86
Предложить исправление Сохранить Отменить
0.241
Предложить исправление Сохранить Отменить
0.09
Предложить исправление Сохранить Отменить
0.955
Предложить исправление Сохранить Отменить
0.085
Предложить исправление Сохранить Отменить
0.29
Предложить исправление Сохранить Отменить
0.855
Предложить исправление Сохранить Отменить
0.248
Предложить исправление Сохранить Отменить
0.1
Предложить исправление Сохранить Отменить
0.95
Предложить исправление Сохранить Отменить
0.095
Предложить исправление Сохранить Отменить
0.3
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
0.255
Предложить исправление Сохранить Отменить
0.11
Предложить исправление Сохранить Отменить
0.945
Предложить исправление Сохранить Отменить
0,104
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
0.12
Предложить исправление Сохранить Отменить
0.94
Предложить исправление Сохранить Отменить
0.113
Предложить исправление Сохранить Отменить
0.31
Предложить исправление Сохранить Отменить
0.845
Предложить исправление Сохранить Отменить
0,262
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
0.32
Предложить исправление Сохранить Отменить
0.84
Предложить исправление Сохранить Отменить
0.269
Предложить исправление Сохранить Отменить
0.13
Предложить исправление Сохранить Отменить
0.935
Предложить исправление Сохранить Отменить
0.121
Предложить исправление Сохранить Отменить
0.33
Предложить исправление Сохранить Отменить
0.835
Предложить исправление Сохранить Отменить
0.275
Предложить исправление Сохранить Отменить
0.14
Предложить исправление Сохранить Отменить
0.93
Предложить исправление Сохранить Отменить
0.13
Предложить исправление Сохранить Отменить
0.34
Предложить исправление Сохранить Отменить
0.83
Предложить исправление Сохранить Отменить
0.282
Предложить исправление Сохранить Отменить
0.15
Предложить исправление Сохранить Отменить
0.925
Предложить исправление Сохранить Отменить
0.13
Предложить исправление Сохранить Отменить
0.35
Предложить исправление Сохранить Отменить
0.825
Предложить исправление Сохранить Отменить
0,289
Предложить исправление Сохранить Отменить
0.16
Предложить исправление Сохранить Отменить
0.92
Предложить исправление Сохранить Отменить
0.147
Предложить исправление Сохранить Отменить
0.36
Предложить исправление Сохранить Отменить
0.82
Предложить исправление Сохранить Отменить
0,295
Предложить исправление Сохранить Отменить
0.17
Предложить исправление Сохранить Отменить
0.915
Предложить исправление Сохранить Отменить
0.155
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
-
Предложить исправление Сохранить Отменить
0.18
Предложить исправление Сохранить Отменить
0.91
Предложить исправление Сохранить Отменить
0.164
Предложить исправление Сохранить Отменить
0.37
Предложить исправление Сохранить Отменить
0.815
Предложить исправление Сохранить Отменить
0.301
Предложить исправление Сохранить Отменить
0.19
Предложить исправление Сохранить Отменить
0.905
Предложить исправление Сохранить Отменить
0.172
Предложить исправление Сохранить Отменить
0.39
Предложить исправление Сохранить Отменить
0.805
Предложить исправление Сохранить Отменить
0.314
Предложить исправление Сохранить Отменить
0.2
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
0.18
Предложить исправление Сохранить Отменить
0.4
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
0.32
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
table 7
Предложить исправление Сохранить Отменить
Cross-sectional areas and mass of reinforcement bars
Предложить исправление Сохранить Отменить
d
Предложить исправление Сохранить Отменить
cross-sectional area (cm.kv.) when the number of rods
Предложить исправление Сохранить Отменить
mass1 m
Предложить исправление Сохранить Отменить
d
Предложить исправление Сохранить Отменить
mm
Предложить исправление Сохранить Отменить
one
Предложить исправление Сохранить Отменить
2
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
five
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
7
Предложить исправление Сохранить Отменить
eight
Предложить исправление Сохранить Отменить
9
Предложить исправление Сохранить Отменить
kg
Предложить исправление Сохранить Отменить
mm
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
0.071
Предложить исправление Сохранить Отменить
0.14
Предложить исправление Сохранить Отменить
0.21
Предложить исправление Сохранить Отменить
0.28
Предложить исправление Сохранить Отменить
0.35
Предложить исправление Сохранить Отменить
0.42
Предложить исправление Сохранить Отменить
0.49
Предложить исправление Сохранить Отменить
0.57
Предложить исправление Сохранить Отменить
0.64
Предложить исправление Сохранить Отменить
0.055
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
0.126
Предложить исправление Сохранить Отменить
0.25
Предложить исправление Сохранить Отменить
0.38
Предложить исправление Сохранить Отменить
0.50
Предложить исправление Сохранить Отменить
0.63
Предложить исправление Сохранить Отменить
0.76
Предложить исправление Сохранить Отменить
0.88
Предложить исправление Сохранить Отменить
1.01
Предложить исправление Сохранить Отменить
1.13
Предложить исправление Сохранить Отменить
0.098
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
five
Предложить исправление Сохранить Отменить
0.196
Предложить исправление Сохранить Отменить
0.39
Предложить исправление Сохранить Отменить
0.59
Предложить исправление Сохранить Отменить
0.79
Предложить исправление Сохранить Отменить
0.98
Предложить исправление Сохранить Отменить
1.18
Предложить исправление Сохранить Отменить
1.37
Предложить исправление Сохранить Отменить
1.57
Предложить исправление Сохранить Отменить
1.77
Предложить исправление Сохранить Отменить
0.154
Предложить исправление Сохранить Отменить
five
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
0.283
Предложить исправление Сохранить Отменить
0.57
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
1.13
Предложить исправление Сохранить Отменить
1.42
Предложить исправление Сохранить Отменить
1.70
Предложить исправление Сохранить Отменить
1.98
Предложить исправление Сохранить Отменить
2.26
Предложить исправление Сохранить Отменить
2.55
Предложить исправление Сохранить Отменить
0.222
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
7
Предложить исправление Сохранить Отменить
0.385
Предложить исправление Сохранить Отменить
0.77
Предложить исправление Сохранить Отменить
1.15
Предложить исправление Сохранить Отменить
1.54
Предложить исправление Сохранить Отменить
1.92
Предложить исправление Сохранить Отменить
2.31
Предложить исправление Сохранить Отменить
2.69
Предложить исправление Сохранить Отменить
3.08
Предложить исправление Сохранить Отменить
3.46
Предложить исправление Сохранить Отменить
0.302
Предложить исправление Сохранить Отменить
7
Предложить исправление Сохранить Отменить
eight
Предложить исправление Сохранить Отменить
0.503
Предложить исправление Сохранить Отменить
1.01
Предложить исправление Сохранить Отменить
1.51
Предложить исправление Сохранить Отменить
2.01
Предложить исправление Сохранить Отменить
2.51
Предложить исправление Сохранить Отменить
3.02
Предложить исправление Сохранить Отменить
3.52
Предложить исправление Сохранить Отменить
4.02
Предложить исправление Сохранить Отменить
4.53
Предложить исправление Сохранить Отменить
0.395
Предложить исправление Сохранить Отменить
eight
Предложить исправление Сохранить Отменить
9
Предложить исправление Сохранить Отменить
0.636
Предложить исправление Сохранить Отменить
1.27
Предложить исправление Сохранить Отменить
1.91
Предложить исправление Сохранить Отменить
2.54
Предложить исправление Сохранить Отменить
3.18
Предложить исправление Сохранить Отменить
3.82
Предложить исправление Сохранить Отменить
4.45
Предложить исправление Сохранить Отменить
5.09
Предложить исправление Сохранить Отменить
5.72
Предложить исправление Сохранить Отменить
0.499
Предложить исправление Сохранить Отменить
9
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
0.785
Предложить исправление Сохранить Отменить
1.57
Предложить исправление Сохранить Отменить
2.36
Предложить исправление Сохранить Отменить
3.14
Предложить исправление Сохранить Отменить
3.93
Предложить исправление Сохранить Отменить
4.71
Предложить исправление Сохранить Отменить
5.50
Предложить исправление Сохранить Отменить
6.28
Предложить исправление Сохранить Отменить
7.07
Предложить исправление Сохранить Отменить
0.617
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
1,510
Предложить исправление Сохранить Отменить
2.26
Предложить исправление Сохранить Отменить
3.39
Предложить исправление Сохранить Отменить
4.52
Предложить исправление Сохранить Отменить
5.65
Предложить исправление Сохранить Отменить
6.79
Предложить исправление Сохранить Отменить
7.92
Предложить исправление Сохранить Отменить
9.05
Предложить исправление Сохранить Отменить
10.18
Предложить исправление Сохранить Отменить
0.888
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
1.539
Предложить исправление Сохранить Отменить
3.08
Предложить исправление Сохранить Отменить
4.62
Предложить исправление Сохранить Отменить
6.16
Предложить исправление Сохранить Отменить
7,69
Предложить исправление Сохранить Отменить
9.23
Предложить исправление Сохранить Отменить
10.77
Предложить исправление Сохранить Отменить
12.31
Предложить исправление Сохранить Отменить
13.85
Предложить исправление Сохранить Отменить
1,208
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
sixteen
Предложить исправление Сохранить Отменить
2,011
Предложить исправление Сохранить Отменить
4.02
Предложить исправление Сохранить Отменить
6.03
Предложить исправление Сохранить Отменить
8.04
Предложить исправление Сохранить Отменить
10.05
Предложить исправление Сохранить Отменить
12.06
Предложить исправление Сохранить Отменить
14.07
Предложить исправление Сохранить Отменить
16.08
Предложить исправление Сохранить Отменить
18.10
Предложить исправление Сохранить Отменить
1.578
Предложить исправление Сохранить Отменить
sixteen
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
2.545
Предложить исправление Сохранить Отменить
5.09
Предложить исправление Сохранить Отменить
7.63
Предложить исправление Сохранить Отменить
10.18
Предложить исправление Сохранить Отменить
12.72
Предложить исправление Сохранить Отменить
15.27
Предложить исправление Сохранить Отменить
17.81
Предложить исправление Сохранить Отменить
20.36
Предложить исправление Сохранить Отменить
22.90
Предложить исправление Сохранить Отменить
1,993
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
3.142
Предложить исправление Сохранить Отменить
6.28
Предложить исправление Сохранить Отменить
9.41
Предложить исправление Сохранить Отменить
12.56
Предложить исправление Сохранить Отменить
15.71
Предложить исправление Сохранить Отменить
18.85
Предложить исправление Сохранить Отменить
21.99
Предложить исправление Сохранить Отменить
25.14
Предложить исправление Сохранить Отменить
28.28
Предложить исправление Сохранить Отменить
2.466
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
3,801
Предложить исправление Сохранить Отменить
7.60
Предложить исправление Сохранить Отменить
11.40
Предложить исправление Сохранить Отменить
15.20
Предложить исправление Сохранить Отменить
19.00
Предложить исправление Сохранить Отменить
22.81
Предложить исправление Сохранить Отменить
26.61
Предложить исправление Сохранить Отменить
30.41
Предложить исправление Сохранить Отменить
34.21
Предложить исправление Сохранить Отменить
2,994
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
4,909
Предложить исправление Сохранить Отменить
9.82
Предложить исправление Сохранить Отменить
14.73
Предложить исправление Сохранить Отменить
19.63
Предложить исправление Сохранить Отменить
24.54
Предложить исправление Сохранить Отменить
29.45
Предложить исправление Сохранить Отменить
34.36
Предложить исправление Сохранить Отменить
39.27
Предложить исправление Сохранить Отменить
44.18
Предложить исправление Сохранить Отменить
3,853
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
28
Предложить исправление Сохранить Отменить
6.158
Предложить исправление Сохранить Отменить
12.32
Предложить исправление Сохранить Отменить
18.47
Предложить исправление Сохранить Отменить
24.63
Предложить исправление Сохранить Отменить
30.79
Предложить исправление Сохранить Отменить
36.95
Предложить исправление Сохранить Отменить
43.10
Предложить исправление Сохранить Отменить
49.26
Предложить исправление Сохранить Отменить
55.42
Предложить исправление Сохранить Отменить
4.83
Предложить исправление Сохранить Отменить
28
Предложить исправление Сохранить Отменить
32
Предложить исправление Сохранить Отменить
8,043
Предложить исправление Сохранить Отменить
16.08
Предложить исправление Сохранить Отменить
24.13
Предложить исправление Сохранить Отменить
32.17
Предложить исправление Сохранить Отменить
40.21
Предложить исправление Сохранить Отменить
48.25
Предложить исправление Сохранить Отменить
56.30
Предложить исправление Сохранить Отменить
64.34
Предложить исправление Сохранить Отменить
72.38
Предложить исправление Сохранить Отменить
6.313
Предложить исправление Сохранить Отменить
32
Предложить исправление Сохранить Отменить
36
Предложить исправление Сохранить Отменить
10.18
Предложить исправление Сохранить Отменить
20.36
Предложить исправление Сохранить Отменить
30,54
Предложить исправление Сохранить Отменить
40.72
Предложить исправление Сохранить Отменить
50.9
Предложить исправление Сохранить Отменить
61.08
Предложить исправление Сохранить Отменить
71.26
Предложить исправление Сохранить Отменить
81.44
Предложить исправление Сохранить Отменить
91.62
Предложить исправление Сохранить Отменить
7.99
Предложить исправление Сохранить Отменить
36
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
12.56
Предложить исправление Сохранить Отменить
25.12
Предложить исправление Сохранить Отменить
37.68
Предложить исправление Сохранить Отменить
50.24
Предложить исправление Сохранить Отменить
62,8
Предложить исправление Сохранить Отменить
75.36
Предложить исправление Сохранить Отменить
87.92
Предложить исправление Сохранить Отменить
100.48
Предложить исправление Сохранить Отменить
113.04
Предложить исправление Сохранить Отменить
9.87
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
CALCULATION OF TARPSETS (TYPE 2) A s =?
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
No. Var
Предложить исправление Сохранить Отменить
M (kNm)
Предложить исправление Сохранить Отменить
in (cm)
Предложить исправление Сохранить Отменить
′ f
Предложить исправление Сохранить Отменить
h′f
Предложить исправление Сохранить Отменить
concrete
Предложить исправление Сохранить Отменить
armature
Предложить исправление Сохранить Отменить
Twi
Предложить исправление Сохранить Отменить
a (cm)
Предложить исправление Сохранить Отменить
h (cm)
Предложить исправление Сохранить Отменить
l (m)
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
one
Предложить исправление Сохранить Отменить
120
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
60
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
6.0
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
2
Предложить исправление Сохранить Отменить
123
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
61
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
6.5
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
136
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
62
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
42
Предложить исправление Сохранить Отменить
6.6
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
130
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
63
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
43
Предложить исправление Сохранить Отменить
6.7
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
five
Предложить исправление Сохранить Отменить
124
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
64
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
44
Предложить исправление Сохранить Отменить
6.8
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
132
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
65
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.6
Предложить исправление Сохранить Отменить
45
Предложить исправление Сохранить Отменить
6.9
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
7
Предложить исправление Сохранить Отменить
118
Предложить исправление Сохранить Отменить
26
Предложить исправление Сохранить Отменить
66
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.7
Предложить исправление Сохранить Отменить
46
Предложить исправление Сохранить Отменить
7.0
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
eight
Предложить исправление Сохранить Отменить
129
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
67
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.8
Предложить исправление Сохранить Отменить
47
Предложить исправление Сохранить Отменить
7.1
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
9
Предложить исправление Сохранить Отменить
137
Предложить исправление Сохранить Отменить
27
Предложить исправление Сохранить Отменить
68
Предложить исправление Сохранить Отменить
13
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.9
Предложить исправление Сохранить Отменить
48
Предложить исправление Сохранить Отменить
7.2
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
119
Предложить исправление Сохранить Отменить
28
Предложить исправление Сохранить Отменить
69
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
4.0
Предложить исправление Сохранить Отменить
49
Предложить исправление Сохранить Отменить
7.3
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
121
Предложить исправление Сохранить Отменить
29
Предложить исправление Сохранить Отменить
70
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
50
Предложить исправление Сохранить Отменить
7.4
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
127
Предложить исправление Сохранить Отменить
thirty
Предложить исправление Сохранить Отменить
71
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
7.5
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
13
Предложить исправление Сохранить Отменить
135
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
72
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
7.6
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
140
Предложить исправление Сохранить Отменить
sixteen
Предложить исправление Сохранить Отменить
73
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
42
Предложить исправление Сохранить Отменить
7.7
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
141
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
60
Предложить исправление Сохранить Отменить
13
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
43
Предложить исправление Сохранить Отменить
7.8
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
sixteen
Предложить исправление Сохранить Отменить
142
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
61
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.6
Предложить исправление Сохранить Отменить
44
Предложить исправление Сохранить Отменить
7.9
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
143
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
62
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.7
Предложить исправление Сохранить Отменить
45
Предложить исправление Сохранить Отменить
8.0
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
144
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
63
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.8
Предложить исправление Сохранить Отменить
46
Предложить исправление Сохранить Отменить
8.1
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
145
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
64
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.9
Предложить исправление Сохранить Отменить
47
Предложить исправление Сохранить Отменить
8.2
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
149
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
65
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
4.0
Предложить исправление Сохранить Отменить
48
Предложить исправление Сохранить Отменить
8.3
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
125
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
66
Предложить исправление Сохранить Отменить
13
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
49
Предложить исправление Сохранить Отменить
8.4
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
126
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
67
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
50
Предложить исправление Сохранить Отменить
8.5
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
129
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
68
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
51
Предложить исправление Сохранить Отменить
8.6
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
138
Предложить исправление Сохранить Отменить
26
Предложить исправление Сохранить Отменить
69
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
8.7
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
140
Предложить исправление Сохранить Отменить
27
Предложить исправление Сохранить Отменить
70
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
52
Предложить исправление Сохранить Отменить
8.8
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
CALCULATION OF TARED SECTIONS. Check M <Msech
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
No. Var
Предложить исправление Сохранить Отменить
M (kNm)
Предложить исправление Сохранить Отменить
in (cm)
Предложить исправление Сохранить Отменить
′ f
Предложить исправление Сохранить Отменить
h′f
Предложить исправление Сохранить Отменить
concrete
Предложить исправление Сохранить Отменить
armature
Предложить исправление Сохранить Отменить
Twi
Предложить исправление Сохранить Отменить
a (cm)
Предложить исправление Сохранить Отменить
h (cm)
Предложить исправление Сохранить Отменить
l (m)
Предложить исправление Сохранить Отменить
As
Предложить исправление Сохранить Отменить
one
Предложить исправление Сохранить Отменить
120
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
60
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
6.0
Предложить исправление Сохранить Отменить
14.3
Предложить исправление Сохранить Отменить
2
Предложить исправление Сохранить Отменить
123
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
61
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
6.5
Предложить исправление Сохранить Отменить
11.5
Предложить исправление Сохранить Отменить
3
Предложить исправление Сохранить Отменить
136
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
62
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
42
Предложить исправление Сохранить Отменить
6.6
Предложить исправление Сохранить Отменить
13.1
Предложить исправление Сохранить Отменить
four
Предложить исправление Сохранить Отменить
130
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
63
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
43
Предложить исправление Сохранить Отменить
6.7
Предложить исправление Сохранить Отменить
15.4
Предложить исправление Сохранить Отменить
five
Предложить исправление Сохранить Отменить
124
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
64
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
44
Предложить исправление Сохранить Отменить
6.8
Предложить исправление Сохранить Отменить
15.2
Предложить исправление Сохранить Отменить
6
Предложить исправление Сохранить Отменить
132
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
65
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.6
Предложить исправление Сохранить Отменить
45
Предложить исправление Сохранить Отменить
6.9
Предложить исправление Сохранить Отменить
12.9
Предложить исправление Сохранить Отменить
7
Предложить исправление Сохранить Отменить
118
Предложить исправление Сохранить Отменить
26
Предложить исправление Сохранить Отменить
66
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.7
Предложить исправление Сохранить Отменить
46
Предложить исправление Сохранить Отменить
7.0
Предложить исправление Сохранить Отменить
11.6
Предложить исправление Сохранить Отменить
eight
Предложить исправление Сохранить Отменить
129
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
67
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.8
Предложить исправление Сохранить Отменить
47
Предложить исправление Сохранить Отменить
7.1
Предложить исправление Сохранить Отменить
16,1
Предложить исправление Сохранить Отменить
9
Предложить исправление Сохранить Отменить
137
Предложить исправление Сохранить Отменить
27
Предложить исправление Сохранить Отменить
68
Предложить исправление Сохранить Отменить
13
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.9
Предложить исправление Сохранить Отменить
48
Предложить исправление Сохранить Отменить
7.2
Предложить исправление Сохранить Отменить
15.3
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
119
Предложить исправление Сохранить Отменить
28
Предложить исправление Сохранить Отменить
69
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
4.0
Предложить исправление Сохранить Отменить
49
Предложить исправление Сохранить Отменить
7.3
Предложить исправление Сохранить Отменить
17.2
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
121
Предложить исправление Сохранить Отменить
29
Предложить исправление Сохранить Отменить
70
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
50
Предложить исправление Сохранить Отменить
7.4
Предложить исправление Сохранить Отменить
14.6
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
127
Предложить исправление Сохранить Отменить
thirty
Предложить исправление Сохранить Отменить
71
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
7.5
Предложить исправление Сохранить Отменить
15.3
Предложить исправление Сохранить Отменить
13
Предложить исправление Сохранить Отменить
135
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
72
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.85
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
41
Предложить исправление Сохранить Отменить
7.6
Предложить исправление Сохранить Отменить
16,1
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
140
Предложить исправление Сохранить Отменить
sixteen
Предложить исправление Сохранить Отменить
73
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
0.9
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
42
Предложить исправление Сохранить Отменить
7.7
Предложить исправление Сохранить Отменить
12.8
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
141
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
60
Предложить исправление Сохранить Отменить
13
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
0.8
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
43
Предложить исправление Сохранить Отменить
7.8
Предложить исправление Сохранить Отменить
13.0
Предложить исправление Сохранить Отменить
sixteen
Предложить исправление Сохранить Отменить
142
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
61
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.6
Предложить исправление Сохранить Отменить
44
Предложить исправление Сохранить Отменить
7.9
Предложить исправление Сохранить Отменить
17.0
Предложить исправление Сохранить Отменить
17
Предложить исправление Сохранить Отменить
143
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
62
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.7
Предложить исправление Сохранить Отменить
45
Предложить исправление Сохранить Отменить
8.0
Предложить исправление Сохранить Отменить
10.9
Предложить исправление Сохранить Отменить
18
Предложить исправление Сохранить Отменить
144
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
63
Предложить исправление Сохранить Отменить
ten
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.8
Предложить исправление Сохранить Отменить
46
Предложить исправление Сохранить Отменить
8.1
Предложить исправление Сохранить Отменить
15.1
Предложить исправление Сохранить Отменить
nineteen
Предложить исправление Сохранить Отменить
145
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
64
Предложить исправление Сохранить Отменить
eleven
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.9
Предложить исправление Сохранить Отменить
47
Предложить исправление Сохранить Отменить
8.2
Предложить исправление Сохранить Отменить
16.3
Предложить исправление Сохранить Отменить
20
Предложить исправление Сохранить Отменить
149
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
65
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
4.0
Предложить исправление Сохранить Отменить
48
Предложить исправление Сохранить Отменить
8.3
Предложить исправление Сохранить Отменить
14.6
Предложить исправление Сохранить Отменить
21
Предложить исправление Сохранить Отменить
125
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
66
Предложить исправление Сохранить Отменить
13
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.0
Предложить исправление Сохранить Отменить
49
Предложить исправление Сохранить Отменить
8.4
Предложить исправление Сохранить Отменить
15.7
Предложить исправление Сохранить Отменить
22
Предложить исправление Сохранить Отменить
126
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
67
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
B25
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.2
Предложить исправление Сохранить Отменить
50
Предложить исправление Сохранить Отменить
8.5
Предложить исправление Сохранить Отменить
18.2
Предложить исправление Сохранить Отменить
23
Предложить исправление Сохранить Отменить
129
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
68
Предложить исправление Сохранить Отменить
15
Предложить исправление Сохранить Отменить
B30
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.3
Предложить исправление Сохранить Отменить
51
Предложить исправление Сохранить Отменить
8.6
Предложить исправление Сохранить Отменить
18.6
Предложить исправление Сохранить Отменить
24
Предложить исправление Сохранить Отменить
138
Предложить исправление Сохранить Отменить
26
Предложить исправление Сохранить Отменить
69
Предложить исправление Сохранить Отменить
12
Предложить исправление Сохранить Отменить
B15
Предложить исправление Сохранить Отменить
AIII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.4
Предложить исправление Сохранить Отменить
40
Предложить исправление Сохранить Отменить
8.7
Предложить исправление Сохранить Отменить
11.3
Предложить исправление Сохранить Отменить
25
Предложить исправление Сохранить Отменить
140
Предложить исправление Сохранить Отменить
27
Предложить исправление Сохранить Отменить
70
Предложить исправление Сохранить Отменить
14
Предложить исправление Сохранить Отменить
IN 20
Предложить исправление Сохранить Отменить
AII
Предложить исправление Сохранить Отменить
1.0
Предложить исправление Сохранить Отменить
3.5
Предложить исправление Сохранить Отменить
52
Предложить исправление Сохранить Отменить
8.8
Предложить исправление Сохранить Отменить
15.0
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
Предложить исправление Сохранить Отменить
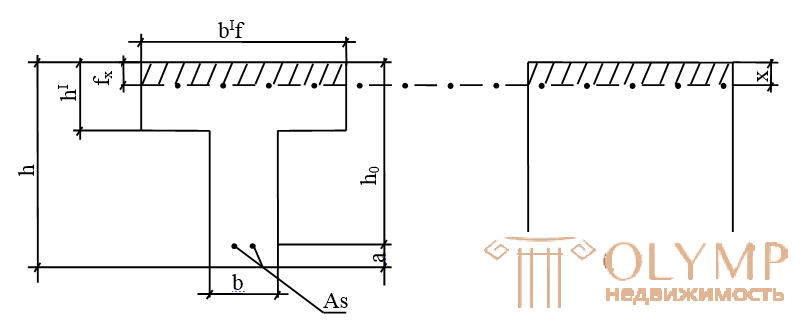

 0, lh
0, lh  h'f <0.1h
h'f <0.1h  h f ')
h f ') 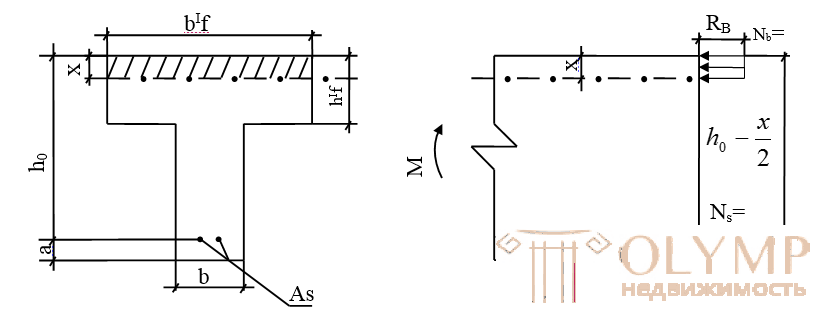
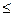 Rb • b'f • x • (ho - x / 2)
Rb • b'f • x • (ho - x / 2)  Rs • As • (ho - x / 2)
Rs • As • (ho - x / 2)  Aomax.
Aomax. 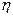 • ho • Rs
• ho • Rs 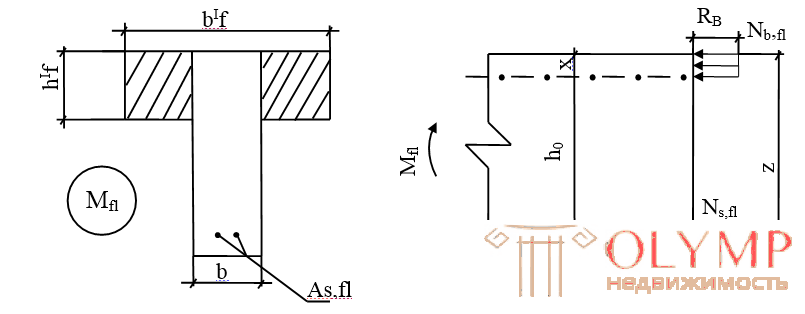
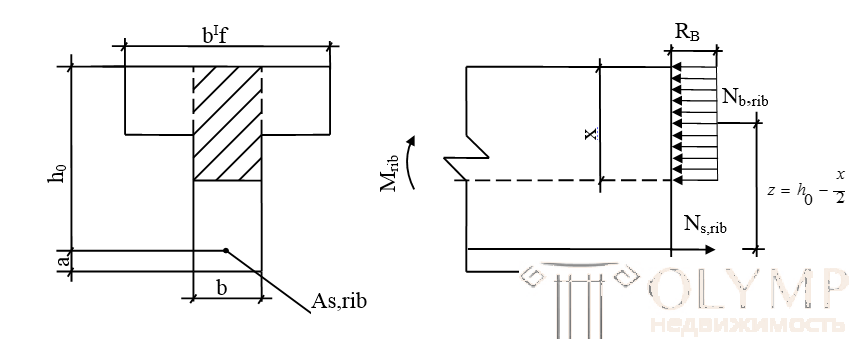
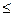 Aomax. (9)
Aomax. (9) 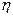 • ho • Rs (100)
• ho • Rs (100) 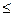 h f ') or (x> h'f) we have, can be as follows:
h f ') or (x> h'f) we have, can be as follows: 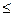 Mh = h'f, then we have the 1st case, if M> Mx = h'f, we have the 2nd case.
Mh = h'f, then we have the 1st case, if M> Mx = h'f, we have the 2nd case. 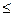 h f ') - as for a rectangular section of width b'f according to formulas (4) and (5)
h f ') - as for a rectangular section of width b'f according to formulas (4) and (5) 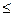 hf '), my moment perceived by the section, is determined
hf '), my moment perceived by the section, is determined 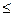 Rb • b'f • x • (ho - x / 2)
Rb • b'f • x • (ho - x / 2) 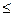 Aomax
Aomax 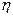 = 0.976 (tab.6 of the application)
= 0.976 (tab.6 of the application) 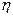 • ho • Rs (100) = 42 • 105 / 0.976 • 37 • 365 (100) = 3.26 cm2
• ho • Rs (100) = 42 • 105 / 0.976 • 37 • 365 (100) = 3.26 cm2 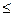 Aomax
Aomax 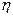 = 0.9
= 0.9 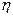 • ho • Rs (100) = 29 • 105 / 0.9 • 37 • 365 (100) = 2.39 cm2
• ho • Rs (100) = 29 • 105 / 0.9 • 37 • 365 (100) = 2.39 cm2 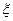 iAoMAh
iAoMAh 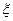 AO,
AO, 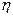
Что бы оставить комментарий войдите
Комментарии (0)