
One of the most important methods of constructing an expressive and integral architectural form is proportioning.
Proportion (lat. Proportio ) - proportionality, a certain ratio of parts between themselves. In modern literature, the concept of proportion is used in three basic meanings:
1. Closest to the notion of proportionality. Indicates the ratio of the basic shape parameters (length, width, height). This is what they mean when they talk about the proportions of any building or structure. The proportion here characterizes an object as a whole, forms the basis of its image.
2. The proportion in architecture (as well as mathematics) is understood as the equality of the relations of quantitative measure of the same objective properties in compared forms or their parts. In mathematical form, recorded as a / b = c / d. This meaning of the concept of "proportion" is used in most of the works on proportioning in architecture. From the mathematical record of such an understanding, it follows that the principle of geometric similarity lies at the basis of the formation of the integral form. The most common example in architecture of applying proportions as equality of mathematical relationships is the formation of a shape based on similar rectangles, the diagonals of which are either parallel (direct proportion) or perpendicular (inverse proportion) (Fig. 33).

Figure 33 - Kinds of proportions based on similar rectangles
The proportion whose average members are equal to each other is called continuous. An example of a continuous proportion is a series of similar rectangles, in which the length of the previous rectangle is equal to the width of the next one.
3. Under the proportion in the architecture understand any pattern in the ratios of quantities that binds the individual parts and form parameters into a coherent whole (the most correct definition). Thus, the proportion in architecture is a concept reflecting the homogeneity (regularity) of changes in a quantitative measure during transitions from one part of a form to another and to a form as a whole.
The first and second definitions of proportion are special cases of the last definition.
In theory and practice of architecture, such types of regular (homogeneous) changes in magnitudes as the arithmetic, harmonic, and geometric progression are well known.
An arithmetic progression is expressed by a series of numbers in which each successive number is greater than the previous one by the same amount. The simplest example of an arithmetic progression is the series of natural numbers 0, 1, 2, 3, 4, 5, etc.
A harmonic progression is a series of numbers that are inverse to a series of numbers of an arithmetic progression, for example: 1/2 , 1/3, 1/4, 1/5, 1/6, 1/7. Relations between neighboring members of the harmonic series as it grows, as well as in the arithmetic progression, change from contrast to nuance.
A geometric progression is a series of numbers in which each successive number is more (or less) than the previous one and the same number of times. For example: 1, 2, 4, 8, 16, ...: 1, 1/2, 1/4, 1/8, 1/16.
Additive series based on summation of numbers are widely used in architecture. For example, in the series of numbers 1, 2, 3, 5, 8, 13, 21, 34, ... (Fibonacci series), each successive member, starting from the 3rd, is equal to the sum of the two previous ones. The relationship between adjacent members of this series, starting from the 5th member, is almost constant and equal to 1.62.
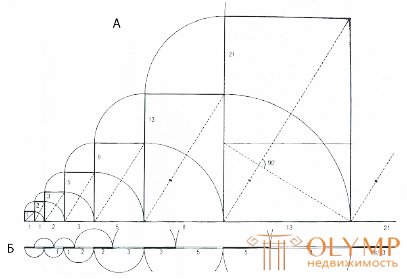
Figure 34 - Linear and two-dimensional interpretation of the Fibonacci series:
a - two-dimensional - rectangles, starting from 8:13, 13:21, acquire proportions of the "golden section" and mutual similarity - their diagonals are parallel and mutually perpendicular; b - linear - stabilization of the proportions of the "golden section", ranging from 3: 5: 8;
5: 8: 13 ...
The term “golden section” was introduced by Leonardo da Vinci for the well-known division of a segment in the so-called “extreme and average ratio”, in which most of it is average proportional to the whole segment and smaller part (Fig. 36).
The golden section used in his work I. Zholtovsky, and Le Corbusier put it in the basis of his "Modulora".
The golden ratio is usually expressed by the number 1.618 or the opposite number 0.618. At the suggestion of T. Cuba and M. Bara, the symbols F and 1 / F were accepted for them. The golden section is the only geometric progression that has the characteristic of an additive series (Ф3 = Ф1 + Ф2).
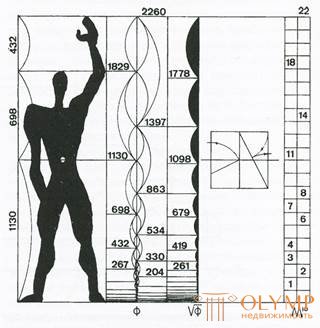
Figure 35 - Modulor Le Corbusier
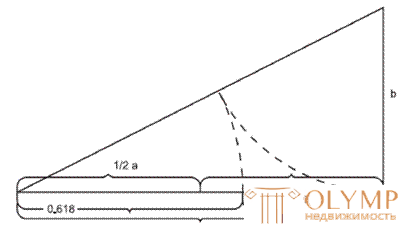
Figure 36 - The division of the segment in the golden section
Proportionation as a method of quantitative coordination of parts and the whole is based on geometric or numerical regularity, which contributes to the achievement of aesthetic integrity, harmony of the volume-spatial form by combining its dimensions into any system.
The features of proportional systems are closely connected with the methods of construction and measurement, which were used by architects of a particular era. In ancient times, proportional systems were obtained by relatively simple geometric constructions based on a triangle, square, rectangle, or circle (Fig. 36).
In ancient Egypt, the system of proportioning was widely used on the basis of the “sacred Egyptian triangle” with a 3: 4: 5 aspect ratio, which allows to get a right angle with the sides expressed in simple integers.
The proportioning system based on the inscribed squares gave a geometric series with the ratio 1: √2, in which the irrational and integer numbers alternated (Fig. 36 (1)). This system was used both in Egypt and in later times, for example in the Middle Ages to build Gothic towers. Also during the Middle Ages, a system of inscribed equilateral triangles was widely used.
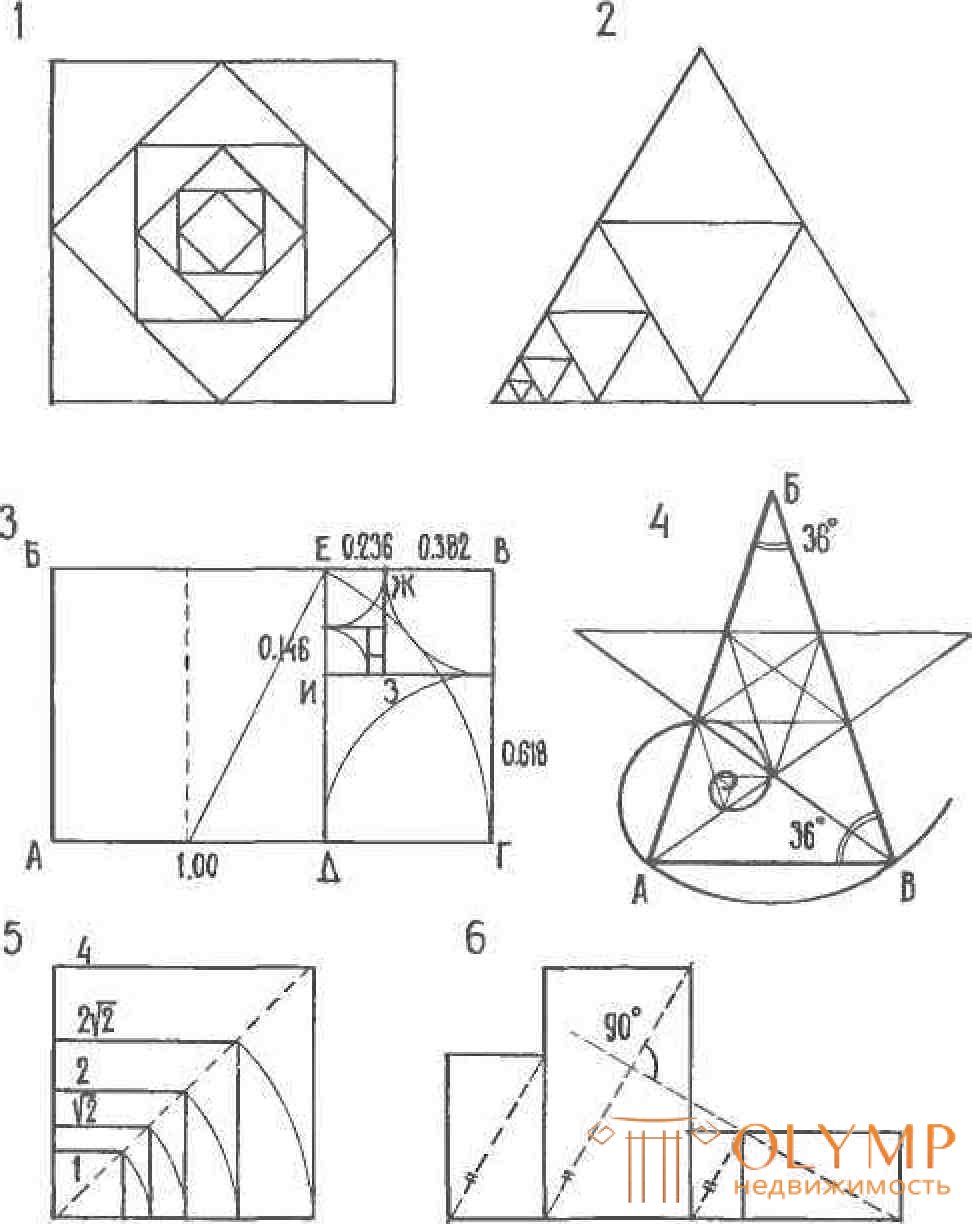
Figure 37 - Proportional systems based on gnomonic constructions on the principle of geometric similarity:
1, 2 - interdependent squares and triangular triangles; 3 - "rolled up" row of rectangles of the "golden section" (ABVG, GDEV, EZHZI. ...);
4 - an isosceles triangle ABC, in which the base and the side are in relation to the "golden section", on its basis a pentagram is built;
5 - proportions based on the ratio of the side and the diagonal of the square 1: √2; 6 - the principle of similarity of rectangles based on the parallelism and perpendicularity of the diagonals
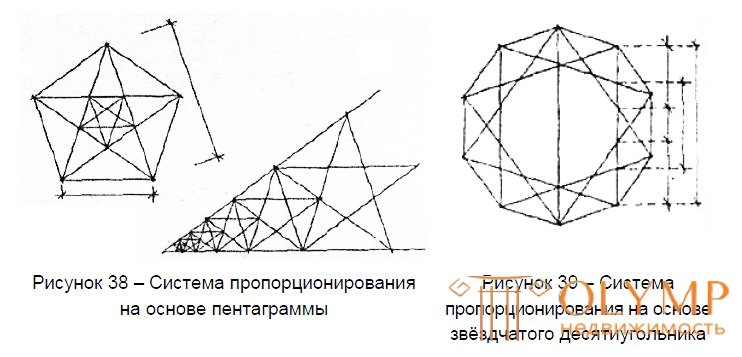
The listed proportioning systems are geometrical; in numerical terms, they are less convenient to use, since they include irrational numbers. However, there are proportional systems based on numerical (arithmetic) methods of matching the parts and the whole; These are so-called modular systems. The simplest example of a modular system is a large-scale grid in which both the general outline and the details of the structure fit. The modular proportioning system assumes the existence of a module - a conventional unit of measurement. The modular system used in our country (EMC) also uses a single module (M = 100 cm), on the basis of which all dimensions taken in construction are obtained by dividing or multiplying.
Proportioning can be used in two main directions: as a method for creating a holistic form and as a method for identifying patterns of construction of already created architectural forms. It should be understood that the patterns identified in the already created architectural forms were not always consciously used by their creators.
Proportionation is a fairly strong, but far from the only means of harmonizing an architectural form, and therefore perfection of proportion alone is not yet the guarantor of obtaining a perfect architectural work.

Figure 40 - Examples of student work (1 course):
1 - proportioning (Fibonacci series);
2 - proportional on the basis of pentagram
Что бы оставить комментарий войдите
Комментарии (0)