
Одним из важнейших методов построения выразительной и целостной архитектурной формы является пропорционирование.
Пропорция (лат. proportio) – соразмерность, определённое соотношение частей между собой. В современной литературе понятие пропорции употребляется в трёх основных значениях:
1. Наиболее близкое к понятию соразмерности. Означает соотношение основных параметров формы (длина, ширина, высота). Именно это значение имеют в виду, когда говорят о пропорциях какого-либо здания, сооружения. Пропорция здесь характеризует объект как целое, составляет основу его образа.
2. Под пропорцией в архитектуре (также, как и математике) понимают равенство отношений количественной меры одних и тех же объективных свойств в сопоставляемых формах или их частях. В математической форме записывают как а/в = c/d. Это значение понятия «пропорция» используется в большинстве работ, посвящённых пропорционированию в архитектуре. Из математической записи такого понимания следует, что здесь в основе образования целостной формы лежит принцип геометрического подобия. Наиболее распространённым в архитектуре примером применения пропорции как равенства математических отношений является образование формы на основе подобных прямоугольников, диагонали которых либо параллельны (прямая пропорция), либо перпендикулярны (обратная пропорция) (рис. 33).

Рисунок 33 – Виды пропорций на основе подобных прямоугольников
Пропорцию, средние члены которой равны между собой, называют непрерывной. Примером непрерывной пропорции может служить ряд подобных прямоугольников, в котором длина предыдущего прямоугольника равна ширине последующего.
3. Под пропорцией в архитектуре понимают любую закономерность в соотношениях величин, которая связывает отдельные части и параметры формы в единое целое (наиболее правильное определение). Таким образом, пропорция в архитектуре есть понятие, отражающее однородность (закономерность) изменений количественной меры при переходах от одной части формы к другой и к форме в целом.
Первое и второе определения пропорции являются частными случаями последнего определения.
В теории и практике архитектуры хорошо известны такие виды закономерных (однородных) изменений величин, как арифметическая, гармоническая и геометрическая прогрессии.
Арифметическая прогрессия выражается рядом чисел, в котором каждое последующее число больше предыдущего на одну и ту же величину. Простейшим примером арифметической прогрессии является ряд натуральных чисел 0, 1, 2, 3, 4, 5 и т. д.
Гармоническая прогрессия – это ряд чисел, обратных ряду чисел арифметической прогрессии, например: 1/2, 1/3, 1/4, 1/5, 1/6, 1/7. Отношения между соседними членами гармонического ряда по мере его возрастания также, как и в арифметической прогрессии, изменяются от контрастных к нюансным.
Геометрическая прогрессия представляет собой ряд чисел, в котором каждое последующее число больше (или меньше) предыдущего в одно и то же число раз. Например: 1, 2, 4, 8, 16, ...: 1, 1/2, 1/4, 1/8, 1/16.
Широко используются в архитектуре аддитивные ряды, построенные на суммировании чисел. Например, в ряде чисел 1, 2, 3, 5, 8, 13, 21, 34, ... (ряд Фибоначчи) каждый последующий член, начиная с 3-го, равен сумме двух предыдущих. Отношение между смежными членами такого ряда, начиная с 5-го члена, практически постоянно и равно 1,62.
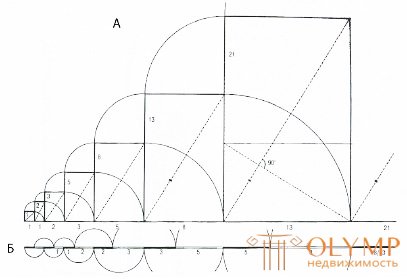
Рисунок 34 – Линейная и двухмерная интерпретация ряда Фибоначчи:
а – двухмерная – прямоугольники, начиная с 8:13, 13:21, приобретают пропорции «золотого сечения» и взаимное подобие – их диагонали параллельны и взаимоперпендикулярны; б – линейная – стабилизация пропорций «золотого сечения», начиная от 3:5:8;
5:8:13...
Термин «золотое сечение» был введён Леонардо да Винчи для известного деления отрезка в так называемом «крайнем и среднем отношении», при котором большая его часть является средней пропорциональной между всем отрезком и меньшей частью (рис. 36).
Золотое сечение использовал в своём творчестве И. В. Жолтовский, а Ле Корбюзье положил его в основу своего «Модулора».
Золотое сечение выражают обычно числом 1,618 или обратным ему числом 0,618. По предложению Т. Куба и М. Бара для них приняты символы Ф и 1/Ф. Золотое сечение – это единственная геометрическая прогрессия, обладающая признаком аддитивного ряда (Ф3 = Ф1 + Ф2).
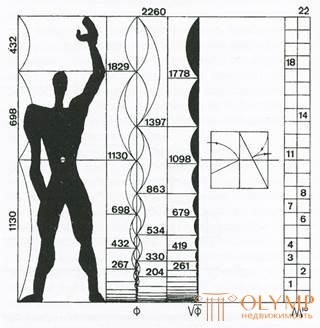
Рисунок 35 – Модулор Ле Корбюзье
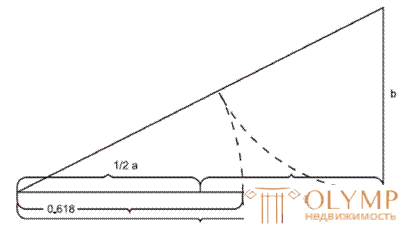
Рисунок 36 – Деление отрезка по золотому сечению
Пропорционирование как метод количественного согласования частей и целого имеет в своей основе геометрическую или числовую закономерность, которая способствует достижению эстетической целостности, гармоничности объёмно-пространственной формы за счёт объединения её размеров в какую-либо систему.
Особенности пропорциональных систем тесно связаны со способами строительства и измерения, которые применялись архитекторами той или иной эпохи. В древности пропорциональные системы получали путём относительно простых геометрических построений на основе треугольника, квадрата, прямоугольника или круга (рис. 36).
В Древнем Египте широко использовалась система пропорционирования на основе «священного египетского треугольника» с соотношением сторон 3:4:5, позволяющего получать прямой угол со сторонами, выраженными в простых целых числах.
Система пропорционирования на основе вписанных квадратов давала геометрический ряд с отношением 1 : √2 , в котором чередовались иррациональные и целые числа (рис. 36 (1)). Эта система использовалась как в Египте, так и в более поздние времена, например в средневековье для построения готических башен. Также в период средневековья широко применялась система вписанных равносторонних треугольников.
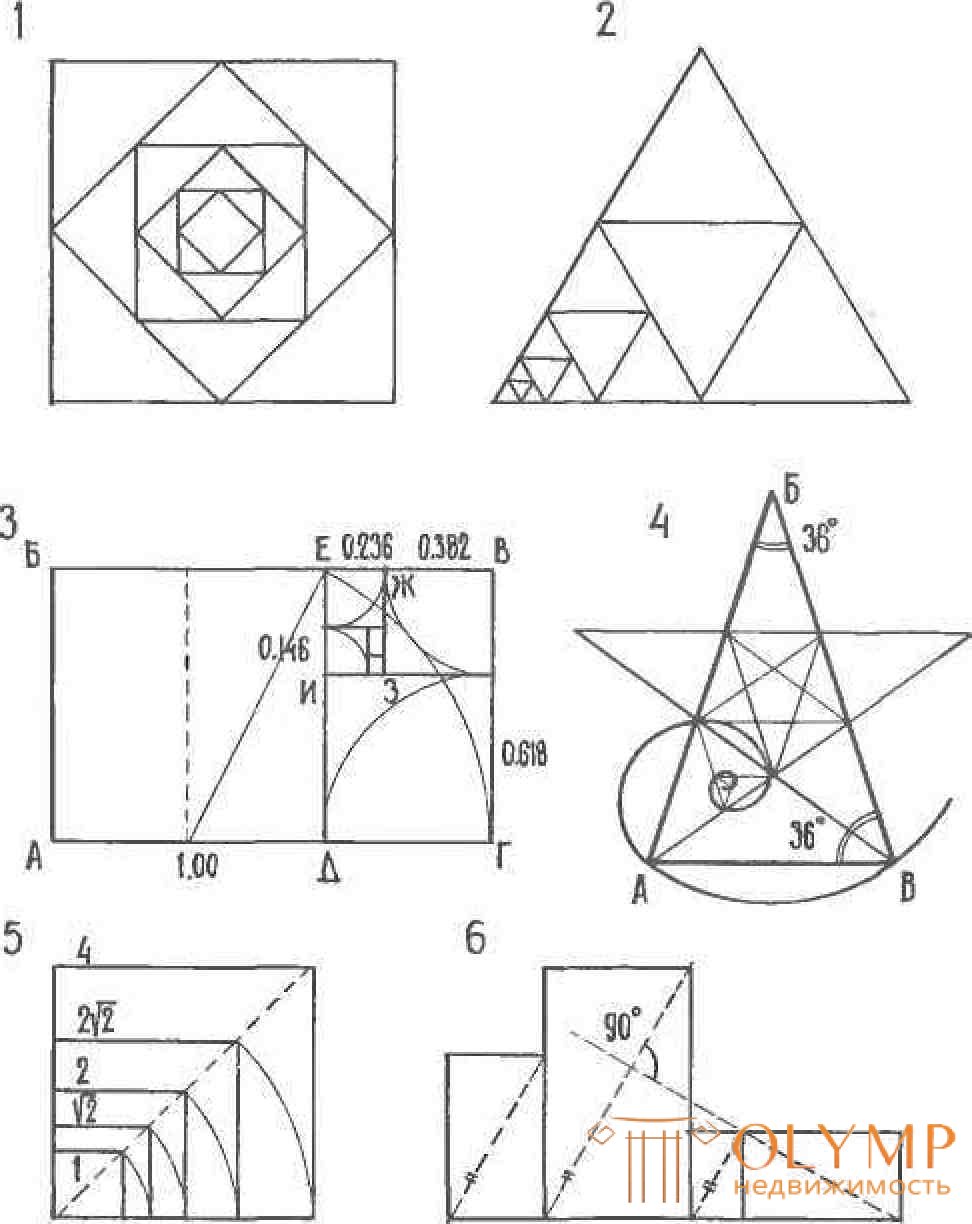
Рисунок 37 – Системы пропорционирования на основе гномонических построений по принципу геометрического подобия:
1, 2 – взаимовписанные квадраты и разносторонние треугольники; 3 – «свёрнутый» ряд прямоугольников «золотого сечения» (АБВГ, ГДЕВ, ЕЖЗИ. …);
4 – равнобедренный треугольник АБВ, в котором основание и сторона находятся в отношении «золотого сечения», на его основе строится пентаграмма;
5 – пропорции на основе соотношения стороны и диагонали квадрата 1 : √2; 6 – принцип подобия прямоугольников на основе параллельности и перпендикулярности диагоналей
Перечисленные системы пропорционирования являются геометрическими, в числовом выражении они менее удобны в использовании, так как включают иррациональные числа. Однако существуют пропорциональные системы, основанные на числовых (арифметических) приёмах согласования частей и целого; это так называемые модульные системы. Простейшим примером модульной системы является масштабная сетка, в которую вписываются как общий абрис, так и детали сооружения. Модульная система пропорционирования предполагает существование модуля – условной единицы измерения. Применяемая в нашей стране модульная система (ЕМС) также использует единый модуль (М = 100 см), на основе которого путём его членения или умножения получают все принятые в строительстве размеры.
Пропорционирование может быть использовано в двух основных направлениях: как метод создания целостной формы и как метод выявления закономерностей построения уже созданных архитектурных форм. При этом следует понимать, что закономерности, выявленные в уже созданных архитектурных формах, далеко не всегда осознанно применялись их создателями.
Пропорционирование – достаточно сильное, но далеко не единственное средство гармонизации архитектурной формы, и поэтому одно только совершенство пропорции ещё не является гарантом получения совершенного архитектурного произведения.

Рисунок 40 – Примеры студенческих работ (1 курс):
1 – пропорционирование (ряд Фибоначчи);
2 – пропорционирование на основе пентаграммы
Что бы оставить комментарий войдите
Комментарии (0)